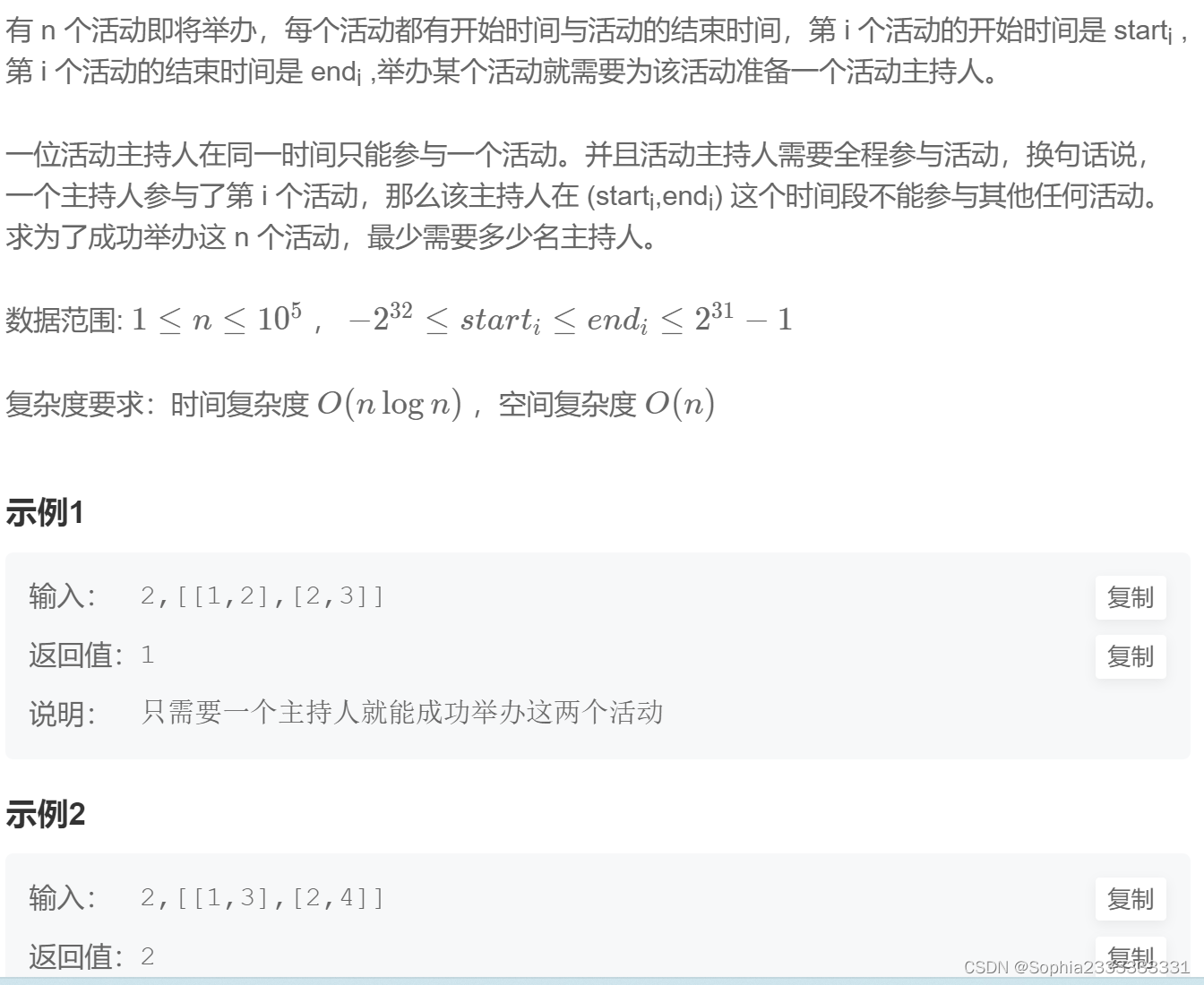
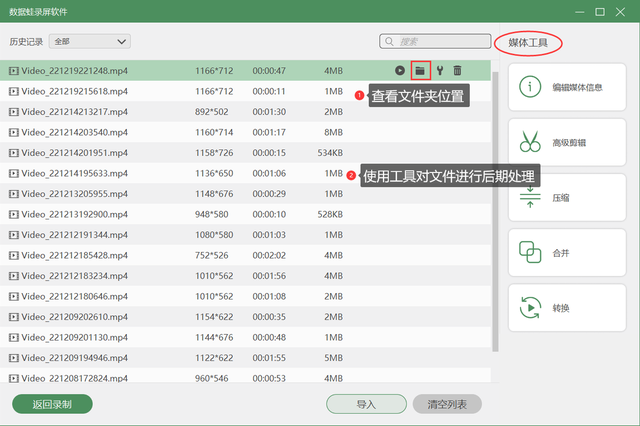
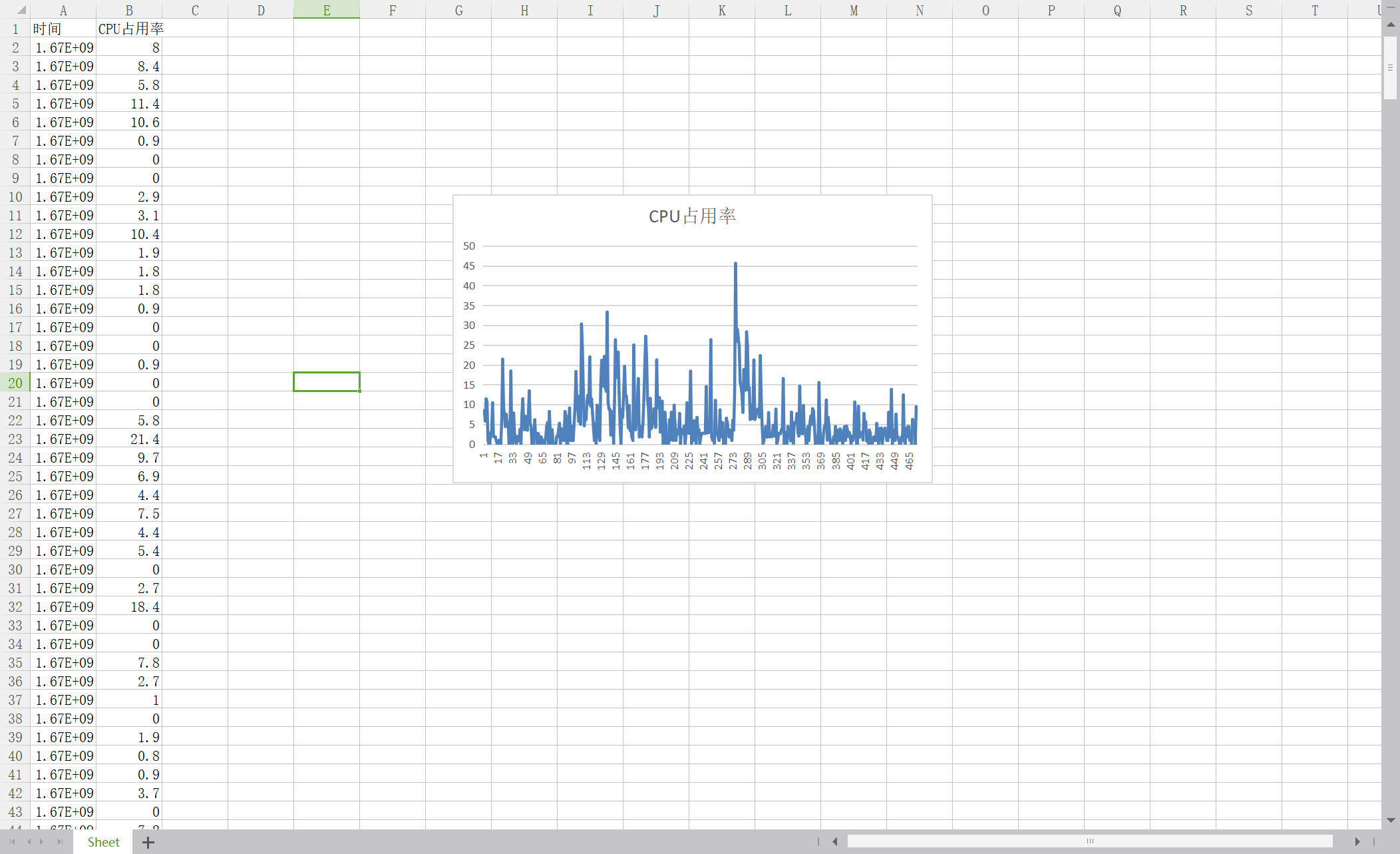
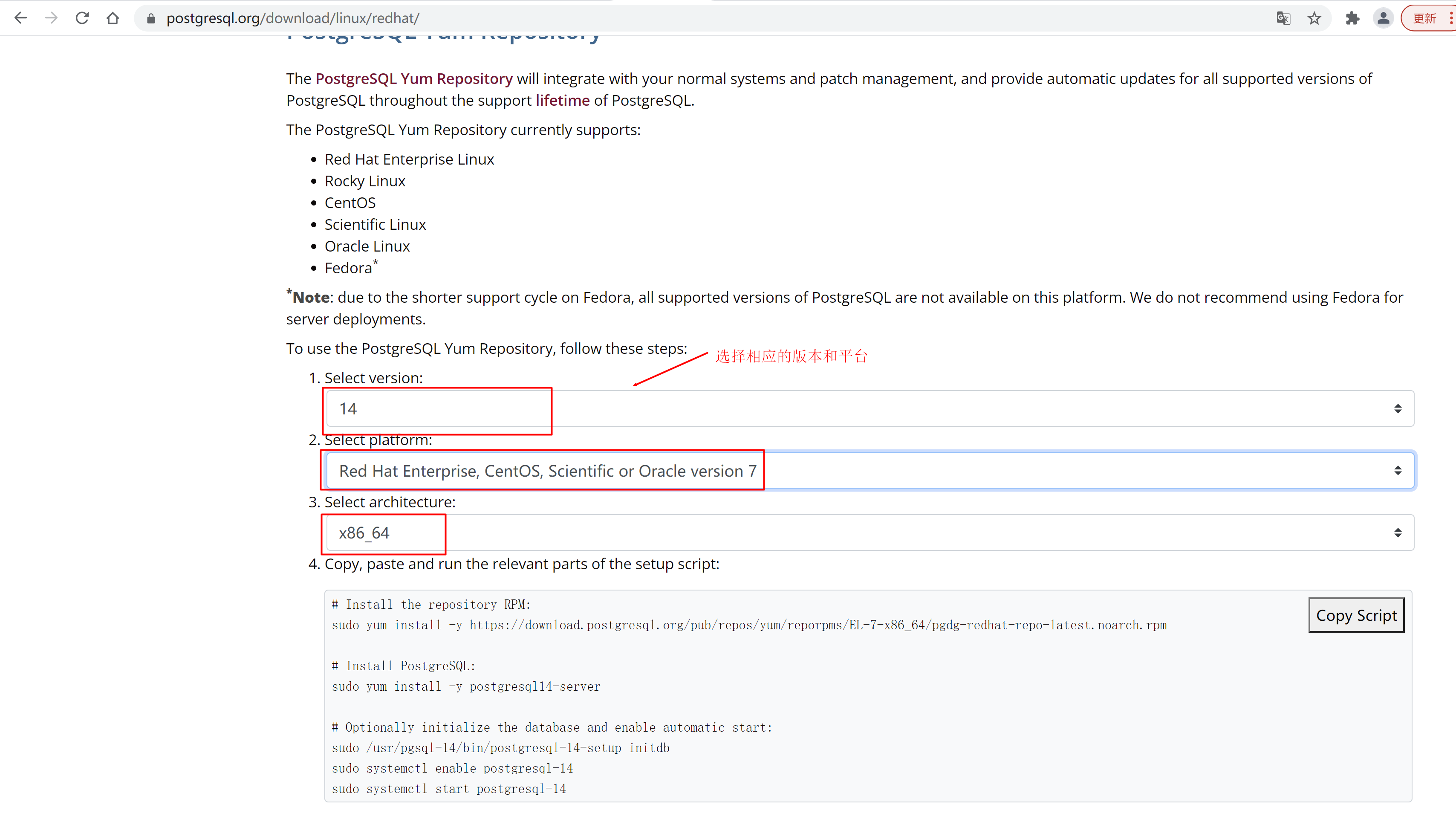
题目链接:343. 整数拆分

1.代码

暴力做法：n前进行组合搜索得出二维数组result存放结果，然后对里面的元素进行乘积，谁最大就是结果

2.递归做法

class Solution {
public:
    int integerBreak(int n) {
        vector<int>f(n + 5, 0);
        f[2] = 1;
        for (int i = 3; i <= n; i++) {
            for (int j = 1; j <= i / 2; j++) {
                f[i] =max(f[i], max(j * (i - j), j * f[i - j]));
            }
        }
        return f[n];
    }
};

2.递归五部曲

1.推导dp数组和其中的含义

题目为求拆分n的乘积最大值，这就是dp数组的含义

2.推导递推公式

f[i]等于什么呢？由题目可以看出，我们先来看后面几个，因为题目没有说，我们不知道前几步到底在哪，k必须大于或等于2，我们就可以看成f[i]是由2个，3个，4个，i个构成的，我们可以先定义一个变量j遍历，确定第一个元素

如果是2个时，f[i] = j *(i - j)

如果是更多个，f[i] = j * f[i - j];

所以我们可以确定这两种类型可以确定f[i]

因为是对j进行for循环，我们需要对每个j求，最后的最大值就是结果

f[i] = max(f[i], max(j * (i - j), j * f[i - j]）)

3.确定初始参数值

我们可以确定必须要分成两份，f[2] = 1

4.确定递推顺序

因为我们需要求f[n]，所以最外面一层是对每个i进行求最大值，直到求到n

第二层就是对每个i求最大值的逻辑，确定第一个参数，其他参数就能够确定了

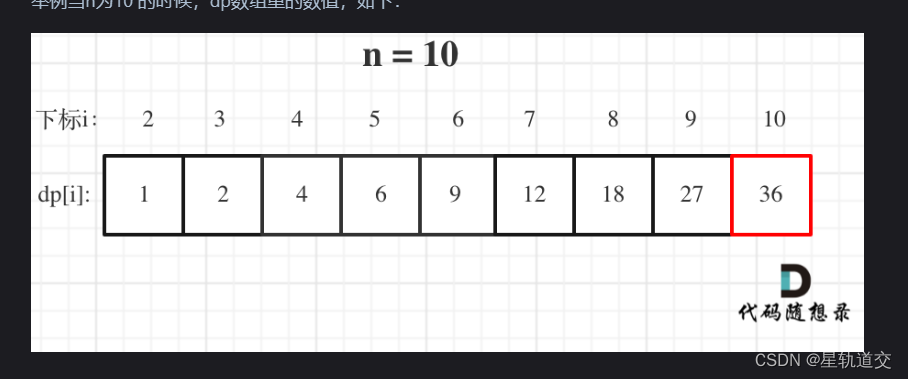
5.举例推导dp数组

可以自己模拟前面几个看一看正确不正确

题目链接：96. 不同的二叉搜索树

1.代码

class Solution {
public:
    int numTrees(int n) {
        vector<int>f(n+1, 0);
        f[0] = 1;
        f[1] = 1;
        f[2] = 2;
        for (int i = 3; i <= n; i++) {
            for (int j = 1; j <= i; j++) {
                f[i] += f[j - 1] * f[i - j];
            }
        }
        return f[n];
    }
};

2.递归五部曲

1.确定dp数组和其下标含义

题目求结点数位n的二叉搜索树的个数，dp[i]就是求结点数位i的搜索树个数

2.确定递推公式

怎么求出的二叉搜索树的个数呢？

如3,对每个结点都有是根节点的可能性，根节点可以是1,2,3。当结点为1时，左子树必须比1小，说明左子树个数为0，右子树为2. 当结点为2时，左右子树各一个结点。当根结点为3时，左边有两个，右边没有,可以推导f[3] = f[0]f[2] + f[1][1] + f[2][0]，就是i为根，比i小的个数*比i大的个数就是以i为根节点的二叉搜索树个数

f[i]：i个结点搜索树的个数，--求出f[i]必须求出从1到i为根结点的二叉搜索树的个数和

3.初始化

介于推导地推公式需要f[0]=1，为0不能，f[1]=1,f[2] =2,其实可以不写这么多，用到哪个写哪个

4.确定递推顺序

因为需要求出f[n]前必须求出f[1-n]所以外面一层循环是求每一个f[i]，里面的循环是有i个结点后以j为根结点的个数，对其求和就是i个结点的二叉搜索树的个数了

5.距离说明dp数组

可以自己距离前面几个模拟一下