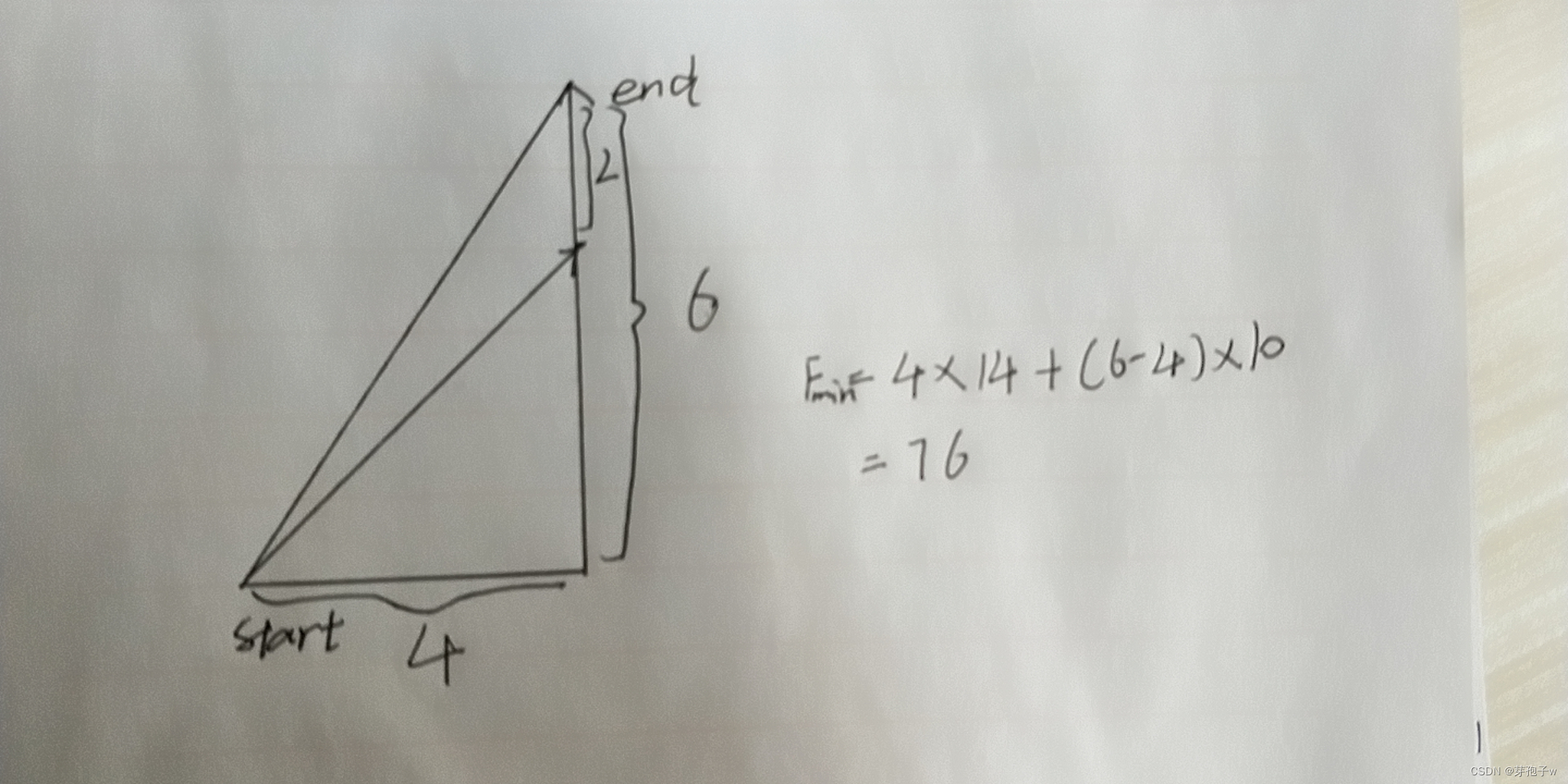哈夫曼树与哈夫曼编码

1.树的带权路径长

百分制成绩转五级制的算法流程图（A/B/C/D/E的人数分别为6/18/21/36/19）

带权路径长 = 路经长 x 权重

树的带权路经长：所有叶结点的带权路径长度之和。

例如：
（a）图中树的带权路经长（进行比较运算的总次数）为——6x1+18x2+21x3+36x4+19x4=325次
（c）图中树的带权路经长为——6x3+18x3+21x2+36x2+19x2=224次

由此可见，对于相同的叶结点，不同结构二叉树的带权路径长可能不同，在本例中，为了提高程序的运行效率，就需要采用带权路径长度最小的二叉树结构，接下来便引出哈夫曼树的概念。

2.哈夫曼树及其构建方法

将m个值{w1,w2,...}作为m个叶结点的权重构造二叉树，则称树的带权路径长最小的二叉树为哈夫曼树，也称最优二叉树。

算法步骤

（1）初始化 ：构造m棵只有一个结点的二叉树，得到一个二叉树集合F={T1,T2...}，Ti的叶结点（也是根结点）的权重为Wi；

（2）选取与合并：新建一个结点tmp，在F中选取根结点权重最小和次小的两棵二叉树Ti和Tj，分别作为tmp的左子树和右子树(顺序可以颠倒），构造一棵二叉树，结点tmp的权重为Ti和Tj的权重之和

（3）删除与加入：在F中删除Ti和Tj，并将以 tmp为根结点的新建二叉树加入F中；

（4）重复步骤(2)和步骤(3)，直到F中只剩下一棵二叉树为止，此时，这棵二叉树就是哈夫曼树。

下图即为哈夫曼树

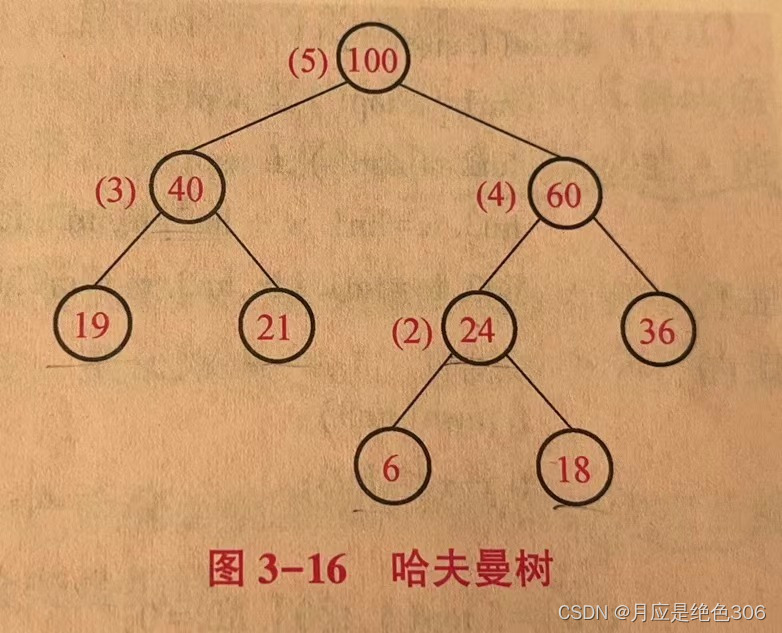
哈夫曼树的特点：

（1）权重越大的叶结点越靠近根结点，权重越小的叶结点越远离根结点；

（2）不存在度为1的结点，具有m个叶结点所构造的哈夫曼树公有2m-1个结点。

#include<iostream>
#include<queue>
using namespace std;
typedef char datatype;
constexpr auto M = 30;;
//由于结点的总数不是太大，因此可以用二叉树左右链数组的表示法做适当的扩展来表示哈夫曼树的特点
//结点定义
typedef struct hutNode {
	datatype data;
	int w, idx; //idx为结点的下标，w表示权重
	int lc, rc;
	bool operator<(const hutNode& hn)const {
		return w > hn.w; //为了使hutNode类型的优先队列中权重较小的优先级较高
	}
}huTree[M<<1];

//由于每一步都要选择集合F中的最小权重结点和次小权重结点，
//且F中的结点是不断更新的，因此可以使用priority_queue
//创建哈夫曼树t：参数m为叶结点的数量，data和w分别为叶结点的数据信息和叶结点的权重
void huTree_create(huTree& t, const datatype data[], int w[], int m) {
	int i;
	hutNode hn1, hn2, hn3;
	priority_queue<hutNode>f;
	for (i = 1; i <= m; i++) {
		t[i].data = data[i - 1], t[i].w = w[i - 1], t[i].idx = i;
		t[i].lc = -1, t[i].rc = -1;
		f.push(t[i]);
	}
		while (f.size() > 1) { //当f只剩下一个元素时结束循环
			hn1 = f.top(), f.pop();
			hn2 = f.top(), f.pop();
			hn3.w = hn1.w + hn2.w, hn3.idx = i;
			hn3.lc = hn1.idx, hn3.rc = hn2.idx;

			f.push(hn3);
			t[i++] = hn3;
		}
		t[0] = f.top(), t[0].idx = 0; //将最终哈夫曼树的根结点的编号设置为0	
}

int main() {
	const char* data = "EDCBA";
	int w[] = { 6,18,21,36,19 };
	huTree t;
	huTree_create(t, data, w, 5);
}

3.哈夫曼编码与解码

哈夫曼编码

哈夫曼树就是哈夫曼在研究变长编码时发明的用于产生满足前缀编码特性的最优变长编码的二叉树。由哈夫曼树所生成的字符集的编码称为哈夫曼编码。

哈夫曼编码依据每个字符在文本中出现的频率（或概率）来构造字符的编码，且用这种编码方法对文本进行编码所得到的二进制编码长度最短，也称为最优编码。

算法——哈夫曼编码的生成方法

功能：对于文本 txt，对其进行编码，使得总文本的总编码长度最短。

算法步骤如下：
(1)统计文本 txt 中各个字符出现的频率(或概率)，并将它们作为叶结点的权重，利用
上述算法构建哈夫曼树，此时哈夫曼树的叶结点代表一个字符；
(2)将哈夫曼树的每个左分支标记为0，右分支标记为 1；
(3)将从根结点到每个叶结点的路径上的各分支的标记连接起来构成一个二进制串，该二进制串即为叶结点所对应字符的编码；
(4)依次将文本中字符转化为编码，并连接为一个字符串，即为该文本的编码。

应用实例：

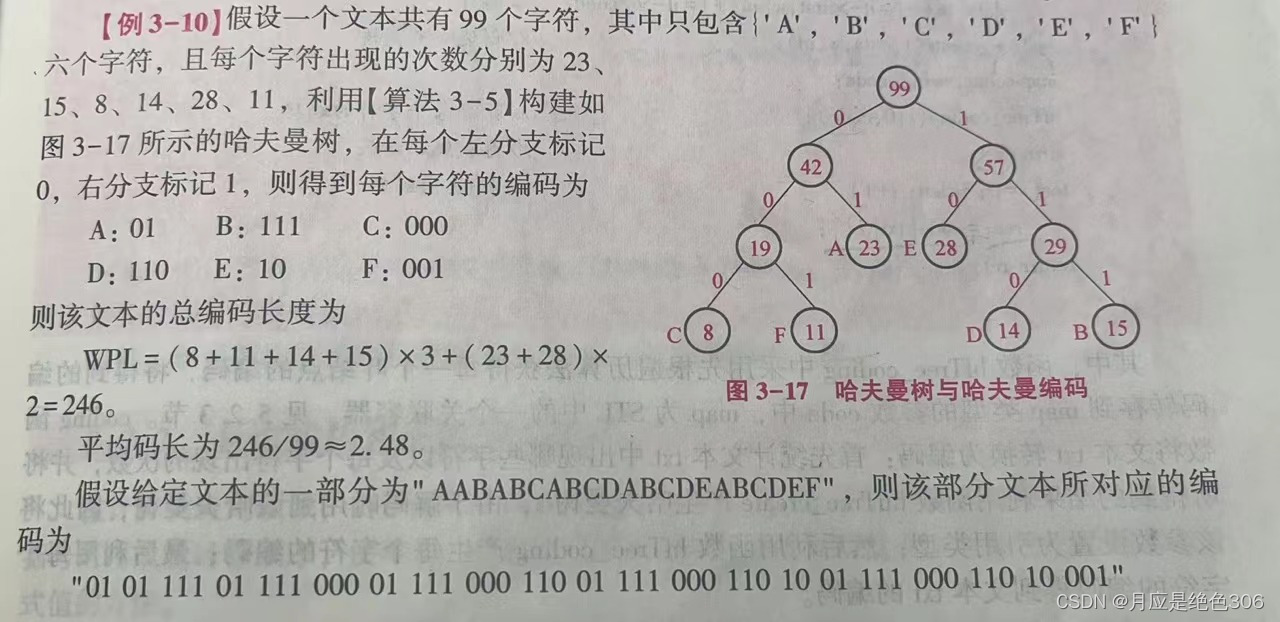
哈夫曼解码

算法：哈夫曼解码

功能：对编码code进行解码，解码结果存放到ret中

步骤：

（1）从哈夫曼树的根结点开始，依次考虑code的每一个字符

（2）如果当前字符为0，则进入左子树，否则进入右子树，并考虑code的下一个字符；

（3）重复步骤（2），当达到叶结点是，将叶结点所对应的字符添加到ret的后面，考虑下一个字符，回到第2步；

（4）当code的所有字符都处理后，解码结束。

注意：对每一个字符的解码都是从哈夫曼树t的根结点开始的，因此当完成一个字符解码之后，需要回到t的根结点。

综上完整代码：

#include<iostream>
#include<queue>
#include<map>
using namespace std;
typedef char datatype;
constexpr auto M = 30;;
//由于结点的总数不是太大，因此可以用二叉树左右链数组的表示法做适当的扩展来表示哈夫曼树的特点
//结点定义
typedef struct hutNode {
	datatype data;
	int w, idx; //idx为结点的下标，w表示权重
	int lc, rc;
	bool operator<(const hutNode& hn)const {
		return w > hn.w; //为了使hutNode类型的优先队列中权重较小的优先级较高
	}
}huTree[M << 1];

//由于每一步都要选择集合F中的最小权重结点和次小权重结点，
//且F中的结点是不断更新的，因此可以使用priority_queue
//创建哈夫曼树t：参数m为叶结点的数量，data和w分别为叶结点的数据信息和叶结点的权重
void huTree_create(huTree& t, const datatype data[], int w[], int m) {
	int i;
	hutNode hn1, hn2, hn3;
	//记住此时的初始化内容，哈夫曼编码用到，无子树为-1，有设置为索引
	priority_queue<hutNode>f; 
	for (i = 1; i <= m; i++) {
		t[i].data = data[i - 1], t[i].w = w[i - 1], t[i].idx = i;
		t[i].lc = -1, t[i].rc = -1;
		f.push(t[i]);
	}
	while (f.size() > 1) { //当f只剩下一个元素时结束循环
		hn1 = f.top(), f.pop();
		hn2 = f.top(), f.pop();
		hn3.w = hn1.w + hn2.w, hn3.idx = i;
		hn3.lc = hn1.idx, hn3.rc = hn2.idx;

		f.push(hn3);
		t[i++] = hn3;
	}
	t[0] = f.top(), t[0].idx = 0; //将最终哈夫曼树的根结点的编号设置为0	
}

//生成一段文本的哈夫曼树编码
//利用哈夫曼树t对每个叶结点进行编码，编码存放在参数code中
/*
	采用先根遍历算法获得每一个业界点的编码，注意弄清回溯过程
*/
void hfTree_coding(huTree t, int cur, map<char, string>& code) {
	static string tmp;
	if (t[cur].lc == -1) {
		code[t[cur].data] = tmp; ///达到叶结点，保存编码
		return;
	}
	tmp += '0';
	hfTree_coding(t, t[cur].lc, code); //左分支
	tmp.erase(tmp.length() - 1);//回溯时将前面所添加的0删除
	tmp += '1';
	hfTree_coding(t, t[cur].rc, code);//右分支
	tmp.erase(tmp.length() - 1);//回溯时将前面所添加的1删除
}

//求txt的编码，并作为函数的返回值
/*
	首先统计文本txt中出现的字符及其次数，然后产生哈夫曼树，
	由于解码用到哈夫曼树，所以参数设置为引用类型；
	然后利用hfTree_coding产生每个字符的编码；
	最后利用每个字符的编码得到文本txt的编码
*/
string coding(huTree& t, string txt) {
	//m为txt中不同字符的数量，w为txt中每个字符出现的次数
	int w[M], m = 0, len = txt.length(), i;
	char data[M];
	map<char, int>ma;
	for (int i = 0; i < len; i++)
		ma [txt[i]]++;//txt中出现的字符
	for (map<char, int>::iterator it = ma.begin(); it != ma.end(); it++)
		data[m++] = it->first, w[m++] = it->second;//转存
	huTree_create(t, data, w, m);//创建哈夫曼树
	map<char, string>code;
	hfTree_coding(t, 0, code);//获得每个字符出现的次数
	string ret; //存放编码结果
	for (int i = 0; i < len; i++) {//存放txt的编码
		ret += code[txt[i]];
	}
	return ret;
}

//哈夫曼解码：解码过程中所得到的每一个字符都对应于哈夫曼树的根结点与某个叶结点之间的一条路径
//利用哈夫曼树t对编码code进行解码，t为编码时所创建的哈夫曼树
string decoding(huTree t, string code) {
	int i, len = code.length();
	string ret;
	hutNode cur = t[0]; //从哈夫曼树的根结点出发
	for (int i = 0; i < len; i++) {
		if (code[i] == '0') //当前编码为‘0’，进入左子树
			cur = t[cur.lc];
		else
			cur = t[cur.rc];
		if (cur.lc == -1) {
			ret += cur.data;
			cur = t[0];
		}
	}
	return ret;
}

int main() {
	string s = "AABCD";
	huTree t;
	string s1 = coding(t, s);
	cout << s1<<endl;
	string s2 = decoding(t, s1);
	cout << s2<<endl;
}