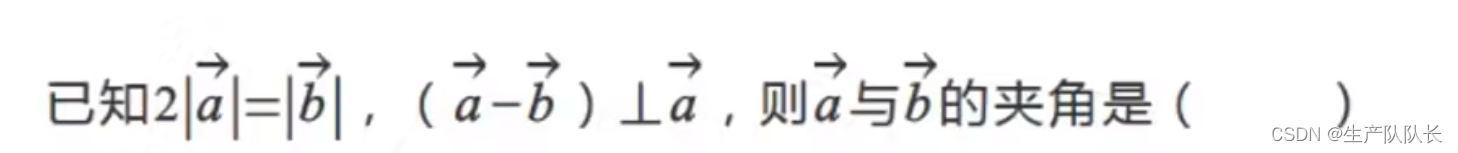高度近视是指近视度数在600度及以上的一种屈光不正的状态。
近视的眼睛必定是变形的。在正常情况下,人的眼球类似球体,但随着近视加深,眼轴变长,眼球体积逐渐增大,整个眼球从圆球型向椭圆球形发展,而眼球壁就像吹泡泡一样,体积增大拉扯着后壁变薄,很容易导致眼底的各种病变。
高度近视分为两种
有可能在成年后趋于稳定,度数不再增加,不伴有不可逆视觉损害的眼底病变,此类我们称之为单纯性高度近视。
2、近视将终身进展,伴有不可逆的视觉损害和眼底病变,此类称为病理性高度近视,其主要原因可能是高度近视引起眼轴不断过度增长。
通过眼底检查能及时发现眼底的问题,高度近视患者眼底常常呈现豹纹状改变,颜色较正常眼底深,出现橘红色,豹纹状改变像是火烧云一片一片的。黄斑部还可出现不规则的、单独或融合的白色萎缩斑。
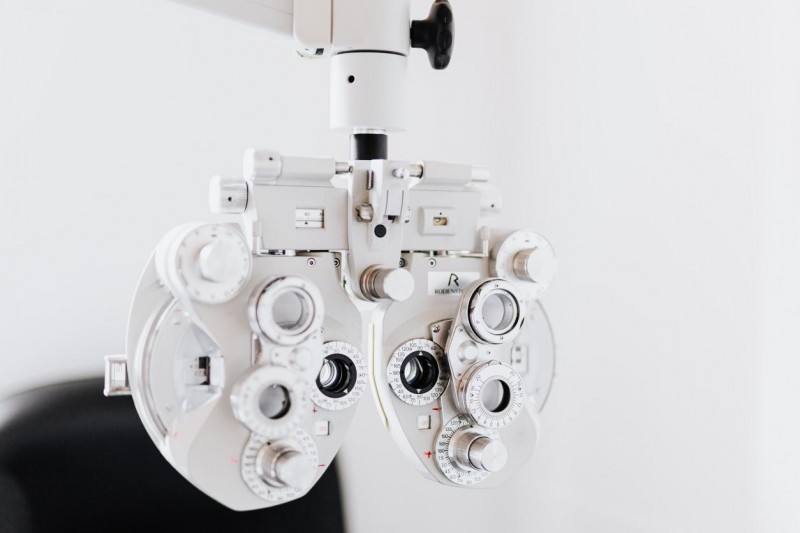
高度近视易发眼底病有:
1、玻璃体液化:眼球轴长变长,玻璃体腔容积扩大,使玻璃体产生囊腔。
2、视网膜出血:眼球内壁视网膜变薄,血液供应障碍会引发视网膜出血。
3、后巩膜葡萄肿:眼球的后极部向后进行扩张。
4、近视性黄斑变性:黄斑区视网膜组织变性、萎缩或发生囊样变性。
视网膜脱离:近视眼的视网膜周边部容易发生变性,视网膜变薄,再加上玻璃体牵拉,引起视网膜脱离。
6、青光眼:眼球扩大眼球壁变薄,视神经穿出眼球壁的视盘处球壁亦较薄,对眼压的抵抗能力下降,当眼球持续存在高眼压引起视神经损害,从而患上继发性青光眼。
当发现眼前黑影飘动,视物模糊、视物变形,闪光感,视力下降,视野缺损,这是发生了眼底疾病,一定要及时到医院就诊!
高度近视眼每年必做检查!
成都爱尔眼科医院眼底病专家胡建斌院长提醒道:高度近视眼不仅有近视度数的增长,还有眼轴的变长,眼底的改变,特别是高度近视黄斑病变及视网膜裂孔、脱离可以严重的威胁视力。
因此建议高度近视患者,每年检查近视度数也散瞳检查眼底,时刻关注眼底情况,做到早发现早治疗。