1. 概述

1.1. 需求

在局部空间（无GPS定位）视频监控过程中，把视频识别到物体位置，投射到空间平面坐标系中，获取物体在局部空间的平面坐标。

1.2. 解决方案

使用图像透视变换技术。

1.3. 透视变换概念

透视变换是指利用透视中心、像点、目标点三点共线的条件，按透视旋转定律使承影面(透视面)绕迹线(透视轴)旋转某一角度，破坏原有的投影光线束，仍能保持承影面上投影几何图形不变的变换。简而言之，就是将一个平面通过一个投影矩阵投影到指定平面上。

透视变换（Perspective Transform）和仿射变换（Affine Transform）在图像还原、局部变化处理方面有重要意义。通常，在2D平面中，仿射变换的应用比较多；在3D平面中，透视变换占领地位较高。两种变换原理相似，结果也相似，可以针对不同场合选择适合方法。

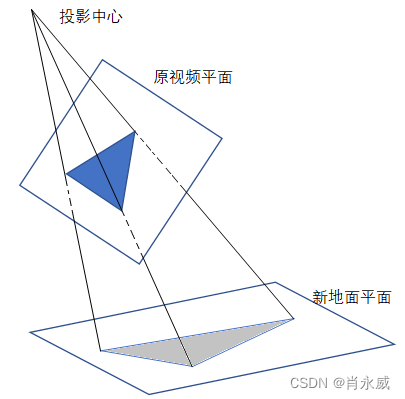
2. 透视变换原理

透视变换：
$$\left(\begin{array}{c}x\\ y\\ z\end{array}\right)=\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\end{array}\right)\left(\begin{array}{c}u\\ v\\ 1\end{array}\right)$$
上述公式中，$u,v$代表原始图像坐标，$x,y$为经过透视变换的图片坐标，其中变换矩阵为$3\times 3$形式。进而可以得到：

$x=a_{11}u+a_{12}v+a_{13}$
$y=a_{21}u+a_{22}v+a_{23}$
$z=a_{31}u+a_{32}v+a_{33}$

在原图上取4点坐标与新图对应，相当于列出方程组，解出变换矩阵。
通过变换矩阵，在输入原图像坐标的情况下，可以直接求解新图平面坐标。
$x^{\prime }=\frac{x}{z}=\frac{a_{11}u+a_{12}v+a_{13}}{a_{31}u+a_{32}v+a_{33}}$
$y^{\prime }=\frac{y}{z}=\frac{a_{21}u+a_{22}v+a_{23}}{a_{31}u+a_{32}v+a_{33}}$

其中，$(x,y)$是原图坐标，$(x’,y’)$是变换后的坐标；$a_{11},a_{12},a_{21},a_{22},a_{31},a_{32}$为旋转量，$a_{13},a_{23},a_{33}$为平移量。因为透视变换是非线性的，所以不能齐次性表示；透视变换矩阵为$3\times 3$。

透视变换的方程组有8个未知数，所以要求解就需要找到4组映射点，四个点就刚好确定了一个三维空间。

3. OpenCV透视变换

3.1. 关于OpenCV透视变换函数

投影变换（Projective mapping）也称透视变换（Perspective transformation）是建立两平面场之间的对应关系， 将图片投影到一个新的视平面（Viewing plane）。

OpenCV 提供了 cv2.warpPerspective 函数实现投影变换的操作。

函数说明：

cv2.getPerspectiveTransform(src, dst[,solveMethod]) → MP
cv2.warpPerspective(src, M, dsize[, dst[, flags[, borderMode[, borderValue]]]]) → dst

• 函数cv2.getPerspectiveTransform 根据图像中不共线的 4 个点在变换前后的对应位置求得 ($3\times 3$) 变换矩阵；
• 函数cv2.warpPerspective 使用该 ($3\times 3$) 变换矩阵即可求出变换后的图像。标量进行加法运算。

参数说明：

• src：变换前图像四边形顶点坐标
• dst：变换后图像四边形顶点坐标
• solveMethod：矩阵分解方法，传递给 cv2.solve 求解变换矩阵 MP
• cv2.DECOMP_LU：选择最优轴的高斯消去法，默认方法
• cv2.DECOMP_SVD：奇异值分解（SVD）方法
• cv2.DECOMP_EIG：特征值分解方法，src 必须对称
• cv2.DECOMP_QR：QR（正交三角）分解
• cv2.DECOMP_CHOLESKY：Cholesky LLT 分解
• MP：透视变换矩阵，3行3列
• dsize： 输出图像的大小，二元元组 (width, height)
• dst：变换操作的输出图像，可选项
• flags：插值方法，整型（int），可选项
• cv2.INTER_LINEAR：线性插值，默认选项
• cv2.INTER_NEAREST：最近邻插值
• cv2.INTER_AREA：区域插值
• cv2.INTER_CUBIC：三次样条插值
• cv2.INTER_LANCZOS4：Lanczos 插值
• borderMode：边界像素方法，整型（int），可选项，默认值为 cv2.BORDER_REFLECT
• borderValue：边界填充模式，可选项，默认值为 0（黑色填充）
• 返回值：dst，透视变换操作的输出图像，ndarray 多维数组

3.2. 透视变换实践设计

为了便于坐标转换，先设定图片像素为坐标，第一步，由图1的标准图，经透视变换为图2，相当于3维空间中某个视角获取到的图像；第二步，再由图2（相当于实际情况下，视频某个空间视角获得的图像）复原，恢复到图3，过程中产生变换矩阵，以此计算新的坐标。

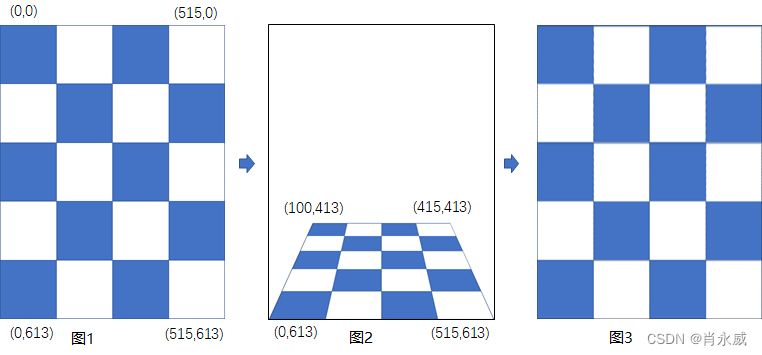
3.2.1. 透视变换图像

此部分代码为由图1变换到图2。

import cv2
import numpy as np

img = cv2.imread("A1.png")
height, width = img.shape[:2]
# print(height, width)

# 变换前的四个点
srcArr = np.float32([[0, 0], [515, 0], [0, 613], [515, 613]])
# 变换后的四个点
dstArr = np.float32([[100, 413], [415, 413], [0, 613], [515, 613]])
# 获取变换矩阵
MM = cv2.getPerspectiveTransform(srcArr, dstArr)
dst = cv2.warpPerspective(img, MM, (width, height))

# 输出保存变换后的图像
cv2.imwrite("pe.png", dst)

3.2.2. 透视变换复原图像及获取像素坐标

import cv2
import numpy as np

img = cv2.imread("pe.png")
height, width = img.shape[:2]
# print(height, width)

# 变换前的四个点
srcArr = np.float32([[100, 413], [415, 413], [0, 613], [515, 613]])
# 变换后的四个点
dstArr = np.float32([[0, 0], [515, 0], [0, 613], [515, 613]])

# 求解获取变换矩阵
MM = cv2.getPerspectiveTransform(srcArr, dstArr)
print(MM)
# 输出复原图像
dst = cv2.warpPerspective(img, MM, (width, height))
cv2.imwrite("A2.png", dst)

# 自定义坐标转换函数
def cvt_pos(u , v, mat):
    x = (mat[0][0]*u+mat[0][1]*v+mat[0][2])/(mat[2][0]*u+mat[2][1]*v+mat[2][2])
    y = (mat[1][0]*u+mat[1][1]*v+mat[1][2])/(mat[2][0]*u+mat[2][1]*v+mat[2][2])
    return (int(x), int(y))
 
# 调用函数
u, v = 100,413
x,y = cvt_pos(u, v, MM)
print(x,y)

其中，变换矩阵MM结果为：

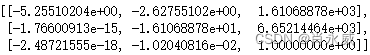
最后，返回像素坐标$(x,y)=(0,0)$。

4. 像素转换到私有坐标系

在实际场景下，经透视复原的图像像素坐标，与实际私有坐标成比例变换，获取比例的方法如下。

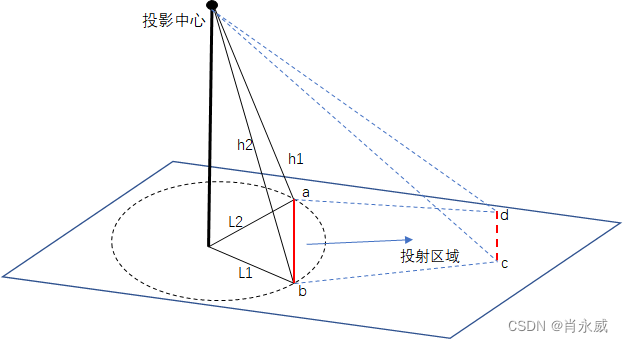
首先，选取变换的基准，在图像上选取四个（a,b,c,d）点中，其中，两个邻居的点a,b作为基准，并且，这两个点的，在图像变换（或求解变换矩阵）时像素坐标不变，其中：
L1 = L2 ， h1 = h2

接着，计算获取ab两点间像素距离与实际平台私有坐标中ab两点的距离，其中：
$k=\frac{D^{\prime }}{D}$
式中的$D^{\prime }$为图像中距离，$D$为私有坐标系平面上的距离。

则，私有坐标系平面上坐标为：$x,y=k{x}^{\prime },k{y}^{\prime }$。

5. 小结

虽然此方案理论及实验可行，但是，工程上实施将比较麻烦，主要涉及到每个视频点的4点定位，以及实际坐标测定。

模拟路况，中间图为”视频角度的图片“，还原投射图的效果如右侧的图片，与左侧原图比较，则图中上面的车，明显变虚。

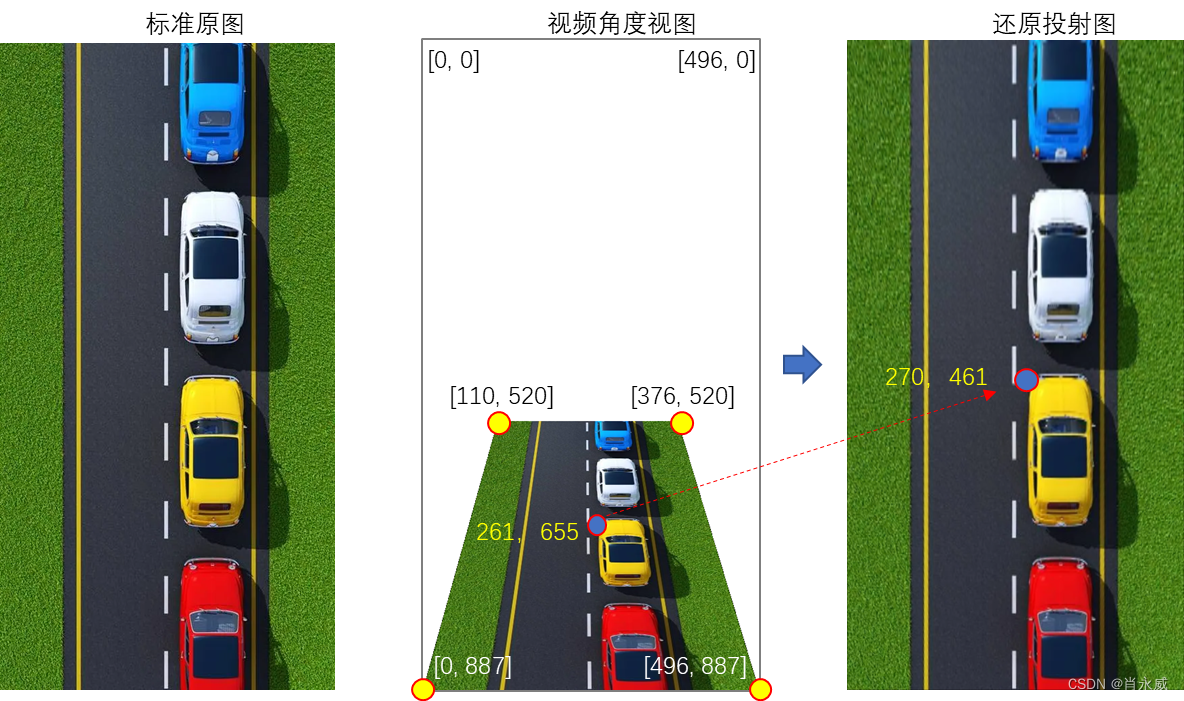
假设标准原图为496、887像素，实际地面宽度为992cm，相当于每个像素为2cm。求解变换矩阵为：

选取中间黄色车左前角，像素坐标为（261，655），还原投射图像素坐标为（270，461），对应实际地面私有坐标为（540，922）cm。

欢迎讨论。

参考：

[1]. 电子小呆比. Opencv-python 求原坐标点透视变换后对应坐标点… CSDN博客. 2022.04
[2]. 小凡. 图像处理的仿射变换与透视变换. 知乎. 2019.04
[3]. 泠山. 仿射变换和透视变换. CSDN博客. 2022.10
[4]. 秋山丶雪绪. Python OpenCV 单目相机标定、坐标转换相关代码（包括鱼眼相机）. CSDN博客. 2022.12
[5]. 王吉吉丫. 图像矫正–python_OpenCV实现透视变换. CSDN博客. 2021.09
[6]. YouCans. 【OpenCV 例程200篇】34. 图像的投影变换（cv2.getPerspectiveTransform）. CSDN博客. 2022.07
[7]. 草原上唱山歌. 几何变换中的仿射变换和透视变换的原理（python）. CSDN博客. 2022.03
[8]. 一马归一码. Python 计算机视觉（五）特别篇 —— 透视变换. CSDN博客. 2022.04