1.概述

（1）所谓遍历 (Traversal) 是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题。遍历是二叉树上最重要的运算之一，是二叉树上进行其它运算之基础。

（2）从二叉树的递归定义可知，一棵非空的二叉树由根结点、左子树和右子树这三个基本部分组成。因此，在任一给定结点上，可以按某种次序执行三个操作：
① 访问结点本身 N；
② 遍历该结点的左子树 L；
③ 遍历该结点的右子树 R；

（3）以上三种操作有六种执行次序：NLR、LNR、LRN、NRL、RNL、RLN。由于前三种次序与后三种次序对称，所以本文只讨论先左后右的前三种次序。然后再根据访问结点操作发生位置命名：
① NLR：前序遍历 (Preorder Traversal，也称为先序遍历)——访问根结点的操作发生在遍历其左右子树之前。
② LNR：中序遍历 (Inorder Traversal)——访问根结点的操作发生在遍历其左右子树之中（间）。
③ LRN：后序遍历 (Postorder Traversal)——访问根结点的操作发生在遍历其左右子树之后。

注意：由于被访问的结点必是某子树的根，所以 N (Node）、L (Left subtree）和 R (Right subtree）又可解释为根、根的左子树和根的右子树。NLR、LNR 和 LRN 分别又称为先根遍历、中根遍历和后根遍历。

（4）除了 NLR、LNR 和 LRN 外，这里再介绍一种遍历方式——层序遍历，即从根节点开始，从上往下、从左往右，一层一层地进行遍历。

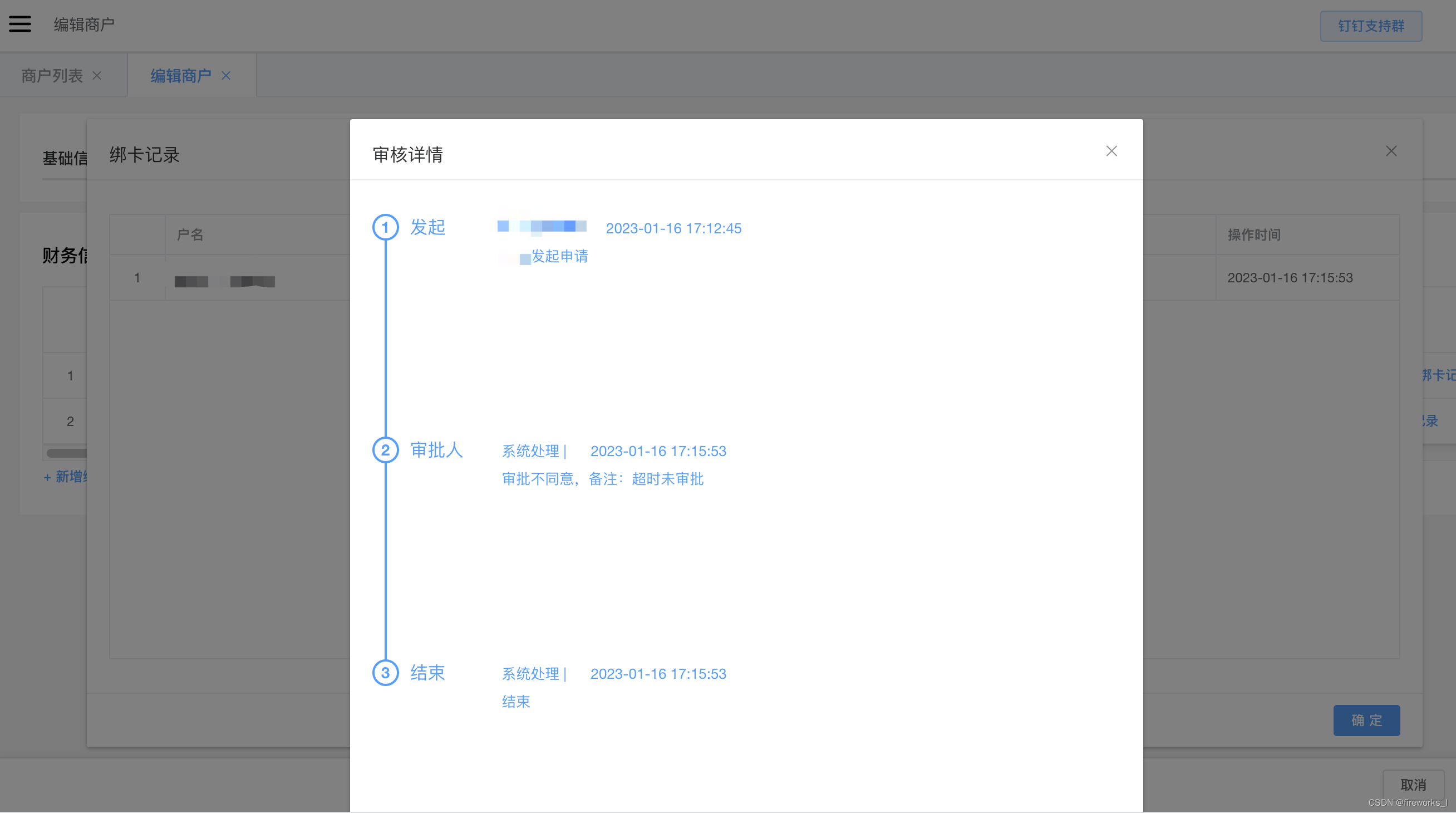
（5）以下面的二叉树为例，来说明上面提到的四种遍历方式。
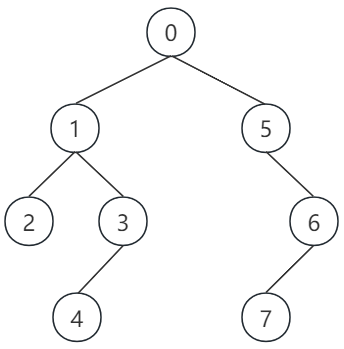
在这里插入图片描述

前序遍历、中序遍历和后序遍历在二叉树上的情况如下所示：

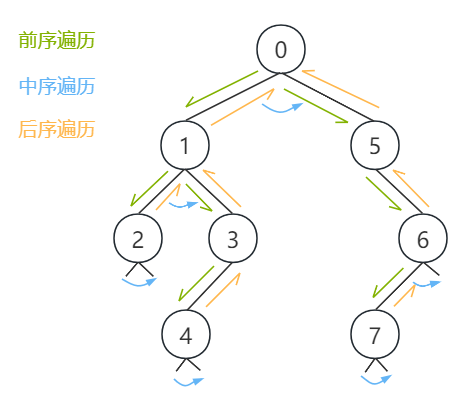
在这里插入图片描述

① 前序遍历的结果为：

0 1 2 3 4 5 6 7

② 中序遍历的结果为：

2 1 4 3 0 5 7 6

③ 后序遍历的结果为：

2 4 3 1 7 6 5 0

④ 层序遍历：

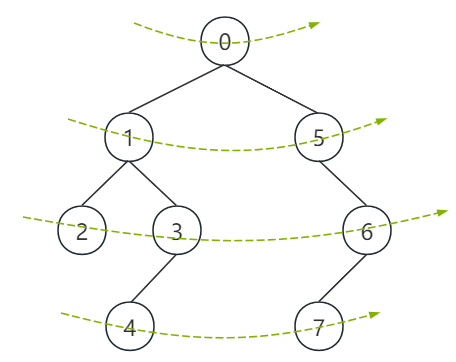
在这里插入图片描述

结果为：

0 1 5 2 3 6 4 7

2.代码实现

2.1.二叉树定义

public class TreeNode {
	//节点值
    int val;
    //左子树
    TreeNode left;
    //右子树
    TreeNode right;
    
    TreeNode() {
    }
    
    TreeNode(int val) {
        this.val = val;
    }
    
    TreeNode(int val, TreeNode left, TreeNode right) {
        this.val = val;
        this.left = left;
        this.right = right;
    }
}

2.2.前序遍历

class Solution {
    
    // res 用于保存前序遍历的结果
    LinkedList<Integer> res = new LinkedList<>();
    
    public List<Integer> preorderTraversal(TreeNode root) {
        traverse(root);
        return res;
    }
    
    public void traverse(TreeNode root) {
        if (root == null) {
            return;
        }
        //将当前根节点的值加入到 res 中
        res.add(root.val);
        //遍历左子树
        traverse(root.left);
        //遍历右子树
        traverse(root.right);
    }
}

2.3.中序遍历

class Solution {
    //res用于保存最终结果
    LinkedList<Integer> res = new LinkedList<>();
    
    public List<Integer> inorderTraversal(TreeNode root) {
        traverse(root);
        return res;
    }
    
    public void traverse(TreeNode root) {
        if (root == null) {
            return;
        }
        //遍历左子树
        traverse(root.left);
        //将当前根节点的值加入到 res 中
        res.add(root.val);
        //遍历右子树
        traverse(root.right);
    }
}

2.4.后序遍历

class Solution {
    //res用于保存最终结果
    LinkedList<Integer> res = new LinkedList<>();
    
    public List<Integer> inorderTraversal(TreeNode root) {
        traverse(root);
        return res;
    }
    
    public void traverse(TreeNode root) {
        if (root == null) {
            return;
        }
        //遍历左子树
        traverse(root.left);
        //遍历右子树
        traverse(root.right);
        //将当前根节点的值加入到 res 中
        res.add(root.val);
    }
}

2.5.层序遍历

class Solution {
    //二叉树的层序遍历
    public List<List<Integer>> levelOrder(TreeNode root) {
        // res 用于保存最终结果
        List<List<Integer>> res = new LinkedList<>();
        if (root == null) {
            return res;
        }
        // queue 保存层序遍历过程中每一层的所有节点
        Queue<TreeNode> queue = new LinkedList<>();
        //最开始的第一层只有根节点，故先将根节点加入到队列中
        queue.offer(root);
        // while 循环控制从上向下方向的遍历
        while (!queue.isEmpty()) {
            // levelSize 记录当前层的节点数量
            int levelSize = queue.size();
            // levelVals 保存当前层的所有节点值
            List<Integer> levelVals = new LinkedList<>();
            // for 循环控制每一层从左向右的遍历
            for (int i = 0; i < levelSize; i++) {
                //poll():返回并删除队列中的第一个元素
                TreeNode curNode = queue.poll();
                levelVals.add(curNode.val);
                //同时将下一层中的所有节点保存到 queue 中
                if (curNode.left != null) {
                    queue.offer(curNode.left);
                }
                if (curNode.right != null) {
                    queue.offer(curNode.right);
                }
            }
            //将当前层的所有节点值加入到 res 中
            res.add(levelVals);
        }
        return res;
    }
}