直线检测算法汇总

1、场景需求

在计算机视觉领域，我们经常需要做一些特殊的任务，而这些任务中经常会用到直线检测算法，比如车道线检测、长度测量等。尽管直线检测的任务看起来比较简单，但是在具体的应用过程中，你会发现这里面还是有很大的优化空间，本文对常用的一些比较经典的直线检测算法进行汇总

2、Hough_line直线检测算法

Hough变换是一个比较有名的计算机视觉处理算法，该算法可以用来做很多的任务，常用的任务包括直线检测、圆检测、椭圆检测等，下面我们将对该算法进行简单的分析并进行代码实战。

2.1 Hough_line实现步骤

步骤1-首先，它创建一个二维数组或累加器（用于保存两个参数的值），并将其初始设置为零；

步骤2-用r来表示行，用θ来表示列；

步骤3-数组的大小取决于你所需要的精度。假设您希望角度的精度为1度，则需要180列（直线的最大度数为180）；

步骤4-对于r，可能的最大距离是图像的对角线长度。因此，取一个像素精度，行数可以是图像的对角线长度。

2.2 Hough_line代码实战

# coding=utf-8
# 导入相应的python包
import cv2
import numpy as np
# 读取输入图片
img = cv2.imread( 'test3.jpg')# 将彩色图片灰度化
gray = cv2.cvtColor(img,cV2.COLOR_BGR2GRAY)# 使用Canny边缘检测
edges = cv2.Canny(gray,50,200,apertureSize = 3)# 进行Hough line直线检测
lines = cv2.HoughLines(edges,1,np.pi/180，200)print(lines)
# 遍历每一个r和theta
for i in range(len(lines)):
	r,theta = lines[i,0，0], lines[i,0，1]
	# 存储cos(theta)的值
	a = np.cos(theta)
	# 存储sin(theta)的值
	b = np.sin(theta)
	# 存储rcos(theta)的值
	X0 = a*r
	# 存储rsin(theta)的值
	y0 = b*r
	# 存储(rcos(theta)-1000sin(theta))的值
	x1 = int(x0 + 1000*(-b))
	# 存储(rsin(theta)+10@Ocos(theta))的值
	y1 = int(y0 + 1000*(a))
	# 存储(rcos(theta)+100Osin(theta))的值
	x2 = int(x0 - 1000*(-b))
	# 存储(rsin(theta)-1000cos(theta))的值
	y2 = int(y0 - 1000*(a))
	# 绘制直线结果
	cv2.line(img,(x1,y1)，(x2,y2)，(0,255,0),2)
	#保存结果
cv2.imwrite('test3_r.jpg', img)
cv2.imshow("result"， img)
cv2.waitKey(0)

2.3 效果展示与分析

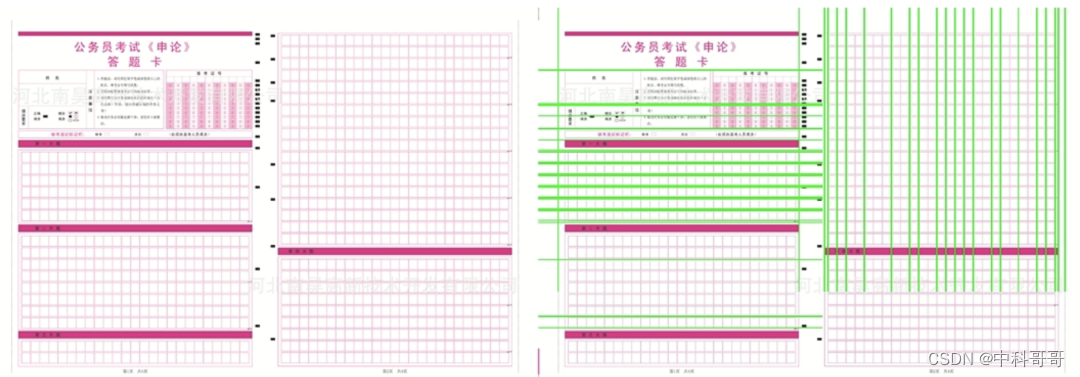
在这里插入图片描述

在这里插入图片描述
上图展示了一些Hough_line算法的直线检测效果。为了验证该算法的有效性，我选择了3个不同的具有挑战性的场景，建筑物、答题卡和门。通过观察上面的结果我们可以知道该算法基本上能够检测出图中的直线，但是检测的结果并不是很好，有很多重复和漏检的情况。除此之外，该算法最大的缺点就是需要根据图片去调节参数，关键的参数是lines = cv2.HoughLines(edges,1,np.pi/180, 200) 中的200，该值设置的越大图片中检测出来的直线数量会越少，你需要根据你自己的测试场景进行调节。

2.4 HoughP_line代码实战

HoughP_line是Hough_line算法的改进版，具有更快的速度和更好的效果。

# coding=utf-8
# 导入相应的python包
import cv2
import numpy as np
# 读取输入图片
img = cv2.imread('test3.jpg')
# 将彩色图片灰度化
gray = cv2.cvtColor(img,Cv2.COLOR BGR2GRAY)
# 使用Canny边缘检测
edges = cv2.Canny(gray,50,200,apertureSize = 3)
# 进行Hough line直线检测
lines = cv2.HoughLinesP(edges,1,np.pi/180，80，30，10)
# 遍每一条直线
for i in range(len(lines)):
	cv2.line(img,(lines[i,0,0l,lines[i,0, 1])，(lines[i,0, 2l,lines[i,0,3])，(0,255,0),2)
# 保存结果
cv2.imwrite('test3_r.jpg',， img)
cv2.imshow("result", img)
cv2.waitKey(0)

2.5 效果展示与分析

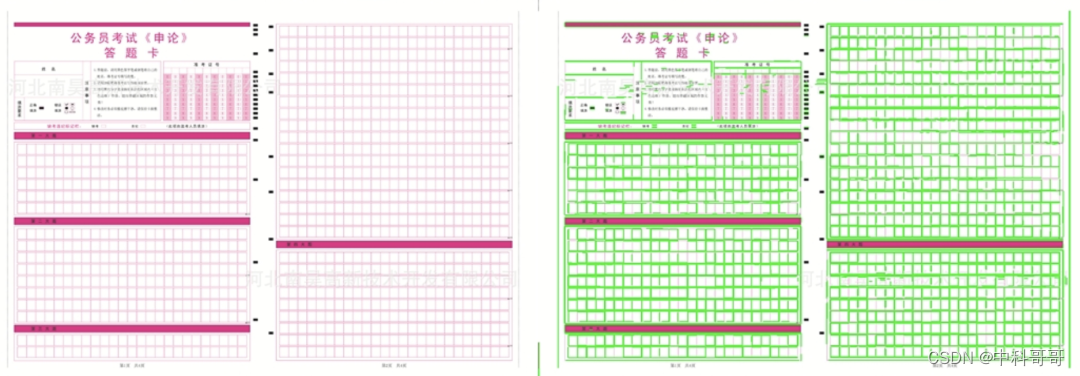
在这里插入图片描述

上图展示了一些HoughP_line算法的直线检测效果。上图都是使用lines = cv2.HoughLinesP(edges,1,np.pi/180, 80, 30, 10) 这个固定的参数来计算出结果的，通过观察我们可以发现，HoughLinesP不仅使用起来比较方便，基本上不需要进行调节参数；除此之外，该算法能够获得更好的直线检测效果。因此，当你想用Hough直线检测算法，建议你优先使用HoughP_line算法。

3、LSD直线检测算法

LSD是opencv中集成的一个直线检测算法，该算法的直线检测效果优于Hough算法，而且具有较好的检测速度，推荐使用。

3.1 LSD算法简介

LSD快速直线检测算法是由Rafael Grompone、Jeremie Jackbowicz、Jean-Michel Morel于2010年发表在PAMI上的文献《LSD:a Line Segment Dectctor》中提出的，该算法时间复杂度较霍夫变换低。LSD算法通过对图像局部分析，得出直线的像素点集，再通过假设参数进行验证求解，将像素点集合与误差控制集合合并，进而自适应控制误检的数量。一般来说，要检测图像中的直线，最基本的思想是检测图像中梯度变化较大的像素点集，LSD算法也正是利用梯度信息和行列线（level-line）来进行直线检测的。

3.2 LSD代码实战

# coding=utf-8
import cv2
import numpy as np
# 读取输入图片
img0 = cv2.imread("test3.jpg")
# 将彩色图片转换为灰度图片
img = cv2.cvtColor(img0,cV2.COLOR BGR2GRAY)
# 创建一个LSD对象
lsd = cv2.createLineSegmentDetector(0)
#执行检测结果
dlines = lsd.detect(img)
# 绘制检测结果
for dline in dlines[@]:
	x0 = int(round(dline[@][O]))
	y@ = int(round(dline[O][1]))
	x1 = int(round(dline[O][2]))
	y1 = int(round(dline[][3]))
	cv2.line(img0，(x0，y0)，(x1,y1)，(0,255,0)，1，Cv2.LINE_AA)
# 显示并保存结果
cv2.imwrite('test3_r.jpg'， img0)
cv2.imshow("LSD"，img@)
cv2.waitKey(0)
cv2.destroyAllWindows()

3.3 效果展示与分析

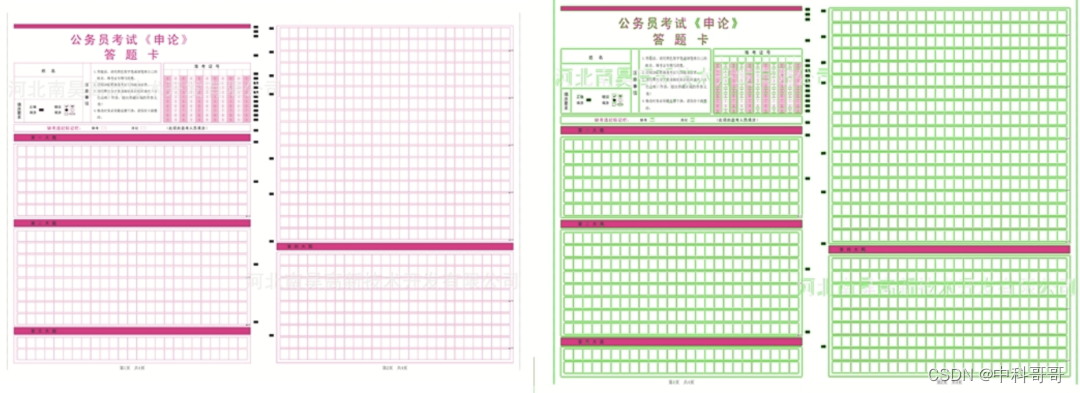
在这里插入图片描述

在这里插入图片描述
上图展示了一些LSD算法的直线检测效果。通过观察上面的结果，我们可以发现该算法的检测结果远远优于Hough和HoughP算法；除此之外，上述的检测结果都是使用LSD算法的默认参数进行执行，如果针对特定的参数进行调节，可以取得更好的结果，这种情况一般是在你的特定需求场景中对默认的一些参数进行微调操作，往往能获得意想不到的结果。
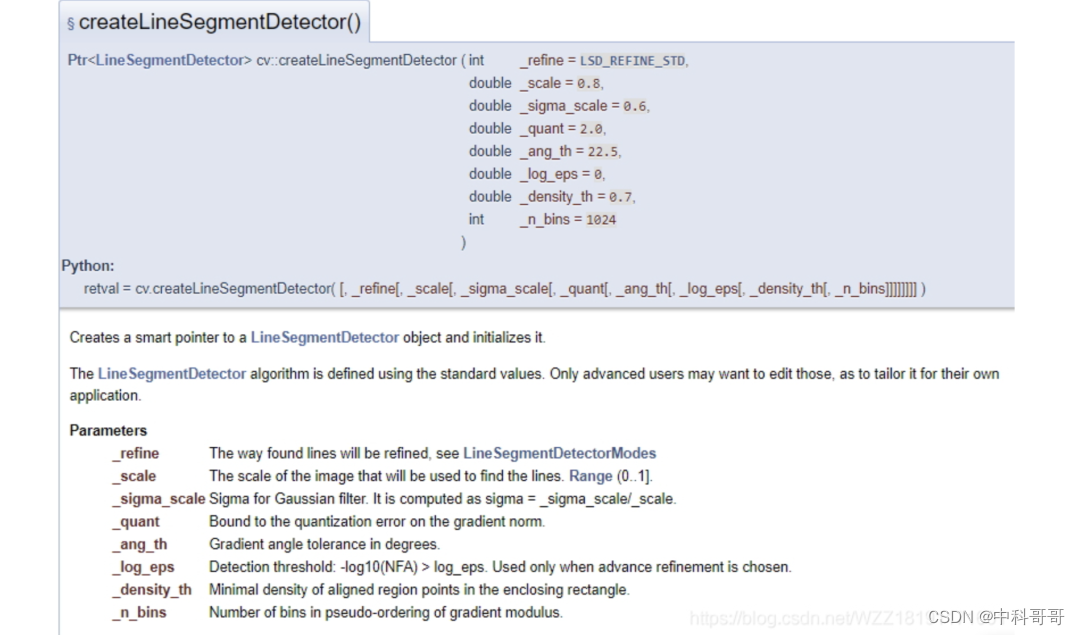
在这里插入图片描述

上图展示了LSD直线检测算法的一些超参数，具体的细节请看该链接。需要说明的是该算法具有3中不同的模式，具体的模式如下图所示，默认情况下使用模式2（即1），但是经过测试我发现模式1（即0）通常输出的效果会更好一些，具体的情况需要你根据你的场景进行分析。

4、FLD直线检测算法

4.1 FLD算法简介

FLD直线检测算法是在该论文中被引入的，该论文中尝试着使用直线特征来代替原始的SURF点特征进行建筑物识别。与点特征进行相比，线特征具有更容易发现和更好的鲁棒性，线特征基本上不会受到光照、遮挡、视角变化的影响。下面展示了该算法的直线检测效果，从图中我们可以看出，线特征比点特征更好一些。

在这里插入图片描述

4.2 FLD算法代码实战

# coding=utf-8
import cv2
import numpy as np
# 读取输入图片
img0 = cv2.imread("test3.jpg")
# 将彩色图片转换为灰度图片
img = cv2.cvtColor(img0,CV2.COLOR BGR2GRAY)
# 创建一个LSD对象
fld = cv2.ximgproc.createFastLineDetector()
# 执行检测结果
dlines = fld.detect(img)
# 绘制检测结果
# drawn_img = fld.drawSegments(img0,dlines，)
for dline in dlines:
	x0 = int(round(dline[@][O]))
	y@ = int(round(dline[O][1]))
	x1 = int(round(dline[0][2]))
	y1 = int(round(dline[O][3]))
	cv2.line(img0，(x0，y0)，(x1,y1)，(0,255,0)，1，cv2.LINE_AA)
# 显示并保存结果
cv2.imwrite('test3_r.jpg', img0)
cv2.imshow("LSD"，img0)
cv2.waitKey(0)
cv2.destroyAllWindows()

4.3 效果展示与分析

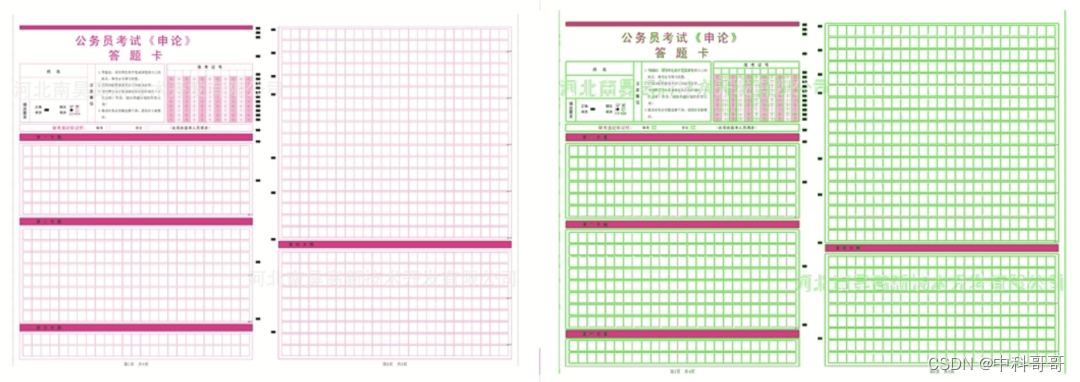
在这里插入图片描述

上图展示了FLD直线检测算法的检测效果。通过观察我们可以发现该算法具有很好的检测效果，基本上可以检测出图中所有的直线，和LSD的性能类似，具体使用哪种算法需要你根据自己的应用场景去进行选择。

5、EDlines直线检测算法

5.1 EDlines算法简介

EDlines直线检测算法是在该论文中提出的。本文提出了一个快速、无参数的线段检测器，命名为EDLines (Akinlar and Topal, 2011)，它产生强大的和准确的结果，比最快的已知线段检测器速度更快，达到11倍；换句话说，the LSD by Grompone von Gioi et al. (2008a,b, 2010). 我们的探测器还包括一个线的验证步骤定于亥姆霍兹原理Helmholtz principle (Desolneux et al., 2008)，这让它控制错误检测的数量。EDLines得到的结果，我们看到的是，LSD非常相似，有所有主要的线段检测，并有极少数误报。此外， EDLines运行实时以炫目的速度为9.45毫秒，约10倍的速度比LSD对给定的图像。

5.2 EDlines算法实现步骤

步骤1-首先，给定一个灰度图像，运行新的边缘检测、边缘绘制（ED）算法，产生一套干净的，像素相邻的链，我们称之为边缘。边缘线段直观地反应对象的边界。

步骤2-然后，利用直线度准则，即最小二乘直线拟合法，从生成的像素链中提取线段。

步骤3-最后，线的验证步骤定于亥姆霍兹原理Helmholtz principle (Desolneux et al., 2008; Grompone von Gioi et al.,2008a)是用来消除虚假线段的检测。

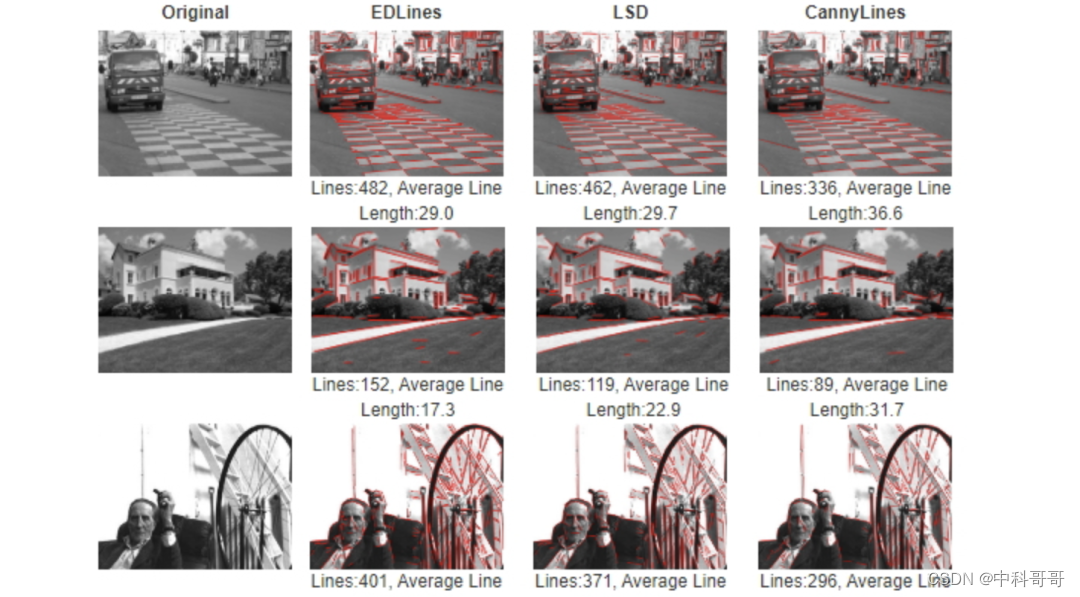
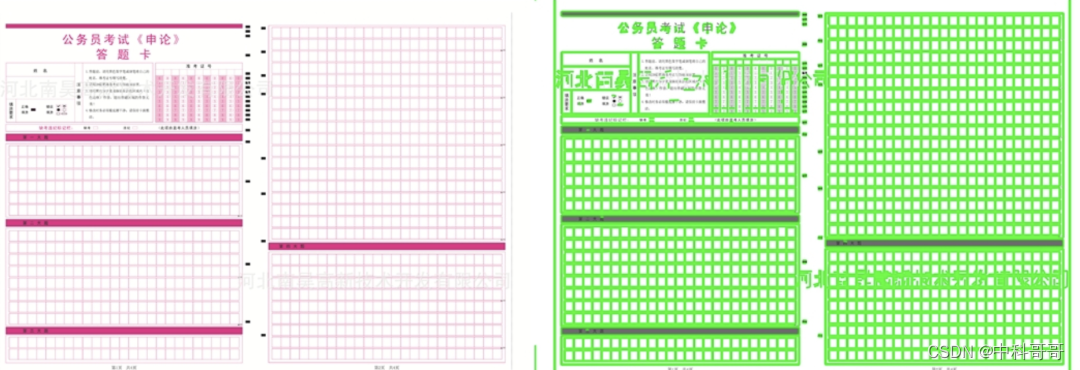在这里插入图片描述

在这里插入图片描述上图展示了EDlines直线检测算法的检测效果。通过上面的观察，我们可以发现：1）该算法能获得和LSD类似的检测结果；2）该算法抑制了一部分小的误检的直线；3）该算法具有更快的运行速度，是LSD的10倍左右。

6、LSWMS直线检测算法

6.1 LSWMS算法简介

LSWMS是一个直线检测算法。本文介绍了一种精确且实时的直线检测方法。以前的直线检测方法都没有使用到图像场景的先验知识，因而不需要对输入的参数进行微调。该算法在检测精度和检测速度之间进行了折中，文中使用了一个高效的采样方法来进行加速处理，然后，文中使用一种快速的直线增长算法基于bresenham算法用改进的mean-shift算法提供精确的线段，同时保持稳健对抗噪音。测试了该策略的性能对于各种各样的图像，将其结果与流行的最新线段检测方法。结果表明，我们的建议优于这些工作同时考虑了结果和处理速度。

在这里插入图片描述
上图展示的是LSWMS论文中的结果。由于作者提供的代码需要在Ubuntu下编译，我没有去做这个工作，如果你感兴趣你可以去运行在本文的3张测试图片上面的效果。

7、CannyLines直线检测算法

7.1 CannyLines算法简介

CannyLines算法在该论文中被提出。本文提出了一种鲁棒的线段检测算法，有效地检测出输入图像中的线段。首先，提出了一种无参数canny算子cannypf，通过自适应地设置传统canny算子的低阈值和高阈值，从输入图像中稳健地提取边缘映射。其次，提出了直接从边缘地图中提取共线点簇的有效像素连接和分割技术，并基于最小二乘法对初始线段进行拟合。第三，通过有效的扩展和合并，生成更长、更完整的线段。最后，根据helmholtz原理对检测到的所有线段进行了验证，该原理同时考虑了梯度方向和幅度信息。在一组有代表性的图像上的实验结果表明，与常用的两种线段检测器lsd和edline相比，我们提出的cannyline线段检测器能够提取出更有意义的线段，特别是在人造场景中。
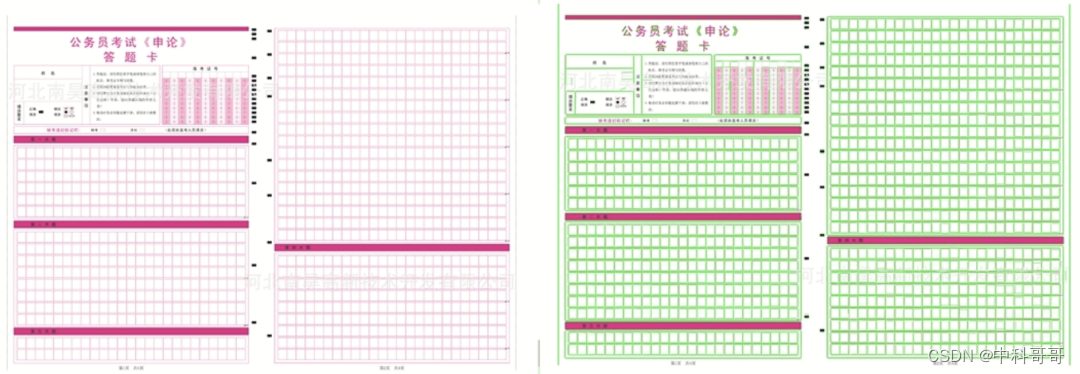
在这里插入图片描述

上图展示了CannyLines直线检测算法的检测效果。通过观察上图我们可以发现该算法能够获得更加准确的检测结果，具有更少的误检。该算法主要是提高了边缘检测的效果，具体的效果如下所示：

8、MCMLSD直线检测算法

8.1 MCMLSD算法简介

MCMLSD算法出自于该论文。论文中提出了一个融合两者优点的概率算法。在第一阶段，使用全局概率hough方法。在第二阶段，在图像域中分析每个检测到的行，以定位在霍夫图中生成峰值的线段。通过将搜索限制在一条直线上，线段的分布线上的点序列可以被建模为马尔可夫链和概率最优标签使用标准动态规划算法精确计算，在线性时间内。马尔可夫假设同时也产生了一种直观的排名方法，它使用估计期望值的边际后验概率线段上正确标记的点的数目。评估由此产生的马尔可夫链边缘线段检测器（mcmlsd）我们开发并应用了一种新的定量方法控制分段不足和分段过量的评估方法。在YorkUrbanDB数据集的评价结果表明，所提出的MCMLSD方法优于以相当大的优势达到最先进水平。

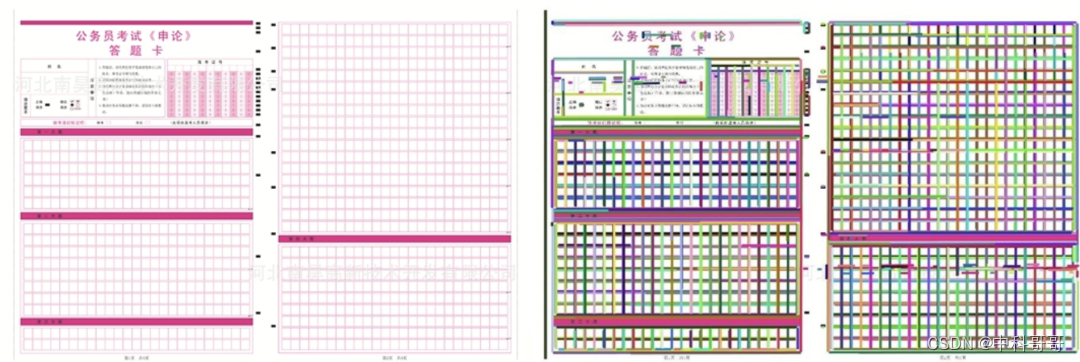
在这里插入图片描述

上图展示了MCMLSD算法的检测效果。通过上面的观察，我们可以发现该算法取得了很好的检测效果，但是美中不足的是该算法的运行速度比较慢，可能也和matlab代码有关吧。

9、LSM直线检测算法

9.1 LSM算法简介

LSM算法不仅仅是一个直线检测算法，同时也是一个直线合并算法。论文中提出了一种合并这些断开的线段的算法，以恢复原始的感知准确的线段。该算法根据角度和空间接近度对线段进行分组。然后将每组中满足新的自适应合并准则的线段对依次合并成一条线段。重复此过程，直到不再合并行段。我们还提出了一种定量比较线段检测算法的方法。在york-urban数据集上的结果表明，与最新的线段检测算法相比，我们的合并线段更接近人类标记的地面真线段。

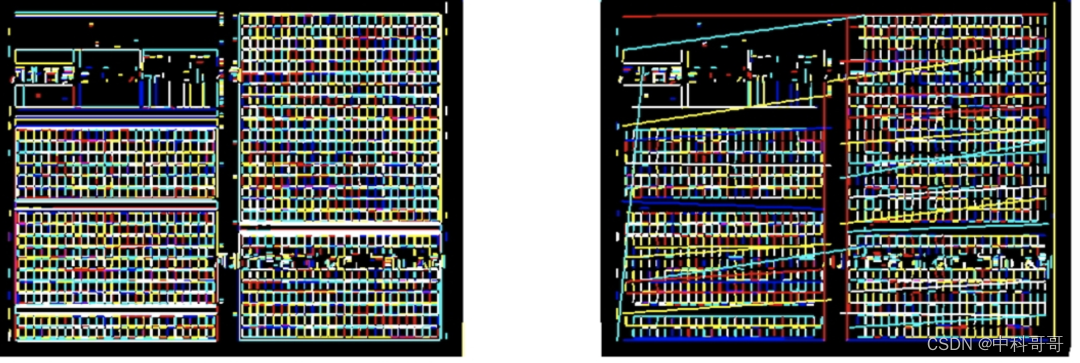
在这里插入图片描述

上图展示了直线检测算法LSM的检测效果。左边一列表示的是LSD的检测结果，右边一列表示的是LSM算法的优化效果，图中不同的颜色表示不同的直线。通过上面的观察，我们可以发现LSM可以将一些间断的直线合并成一条更长的直线，这在现实场景中具有很大的用处，但是我们也会发现LSM算法会错误的将一些直线进行合并，会造成一些误差。

10、总结

本文对比较经典的直线检测算法进行了总结和分析。对于直线检测这个任务而言，它在现实场景中具有很多的应用，对于一个具体的场景，你可以根据自己的需要从本文中选择出一个合适的直线检测算法进行应用，如果你的场景比较简单，HoughP_line算法可能就可以满足你的要求；如果你同时对速度和精度有要求，可以选择使用EDlines等；如果你需要获得尽可能长的直线，那么建议你使用LSM直线检测算法。总而言之，最适合你的场景的算法才是最好的算法。

在这里插入图片描述