目录

问题描述：

实现代码与解析：

反中序遍历法：

原理思路：

迭代：

原理思路：

---

问题描述：

        给出二叉 搜索 树的根节点，该树的节点值各不相同，请你将其转换为累加树（Greater Sum Tree），使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。

提醒一下，二叉搜索树满足下列约束条件：

• 节点的左子树仅包含键 小于 节点键的节点。
• 节点的右子树仅包含键 大于 节点键的节点。
• 左右子树也必须是二叉搜索树。

注意：本题和 1038: 力扣 相同

示例 1：

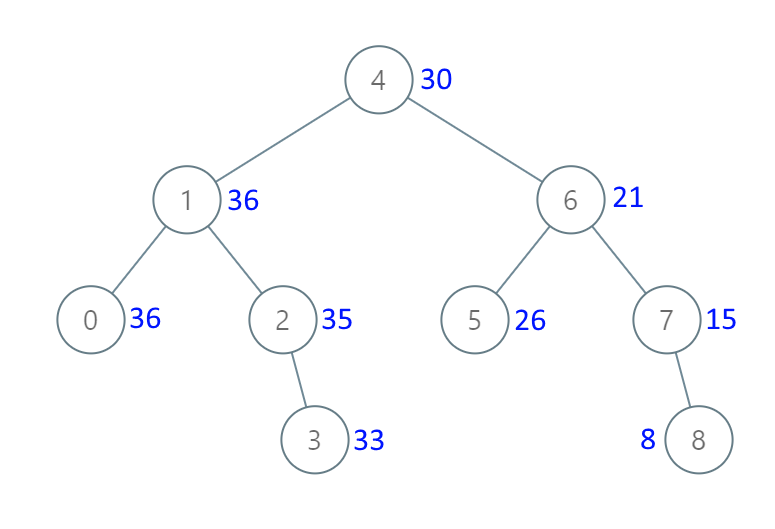
输入：[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出：[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]

示例 2：

输入：root = [0,null,1]
输出：[1,null,1]

示例 3：

输入：root = [1,0,2]
输出：[3,3,2]

示例 4：

输入：root = [3,2,4,1]
输出：[7,9,4,10]

实现代码与解析：

反中序遍历法：

class Solution {
public:
    void traversal(TreeNode* cur,int& sum)
    {
        if(cur==NULL) return;
        traversal(cur->right,sum);
        sum=sum+cur->val;//求和
        cur->val=sum;//赋值
        traversal(cur->left,sum);
        return;
    }
    TreeNode* convertBST(TreeNode* root) 
    {
        int sum=0;
        traversal(root,sum);
        return root;
    }
};

原理思路：

        简单题，根据题意，可以看出节点值累加的顺序是右中左，所以我们反向去中序遍历，同时给结点赋值即可，只不过反向中序遍历可能不太符合一般的解题思路，所以可能会想不到，想到的话就很好写了。

迭代：

class Solution {
public:
    int sum; // 记录累加值
    void traversal(TreeNode* root) 
    {
        stack<TreeNode*> st;
        TreeNode* cur = root;
        while (cur != NULL || !st.empty()) 
        {
            if (cur != NULL) 
            {
                st.push(cur);
                cur = cur->right;   
            } 
            else 
            {
                cur = st.top();    
                st.pop();
                cur->val += sum;
                sum = cur->val;
                cur = cur->left;    
            }
        }
    }
    TreeNode* convertBST(TreeNode* root) 
    {
        traversal(root);
        return root;
    }
};

原理思路：

        与递归同，也就是反向中序迭代的代码改一改而已。