1 算子范数【从属范数】

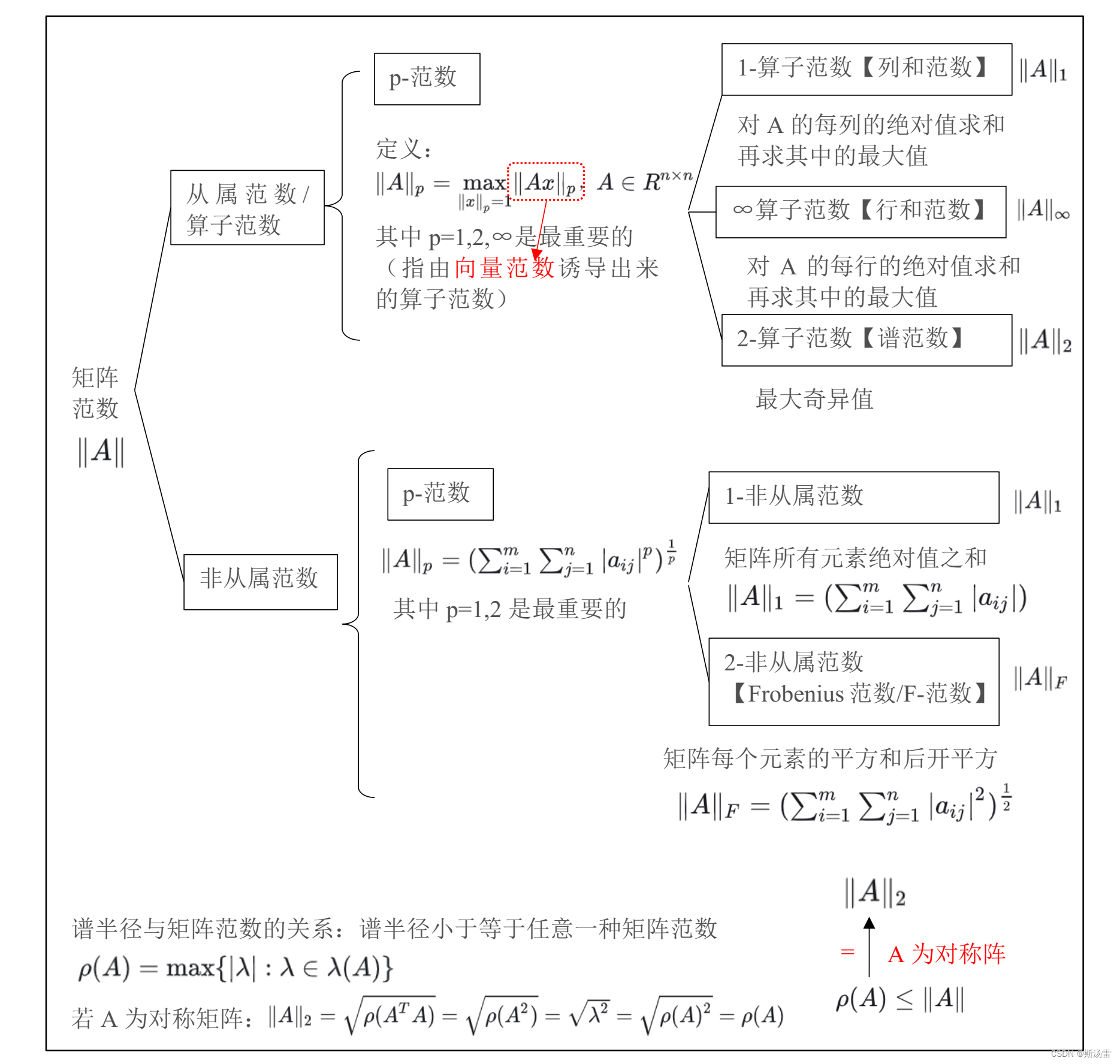
1.1  1-算子范数【列和范数】 ：即对A的每列的绝对值求和再求其中的最大值

1.2  ∞-算子范数【行和范数】即对 A 的每行的绝对值求和再求其中的最大值

1.3  2-算子范数【谱范数】 学过奇异值分解就知道谱范数是最大奇异值/ 二次型的最大特征值

 2 非从属范数 

2.1-非从属范数：即矩阵所有元素绝对值之和

2.2-非从属范数【Frobenius范数/F-范数】即矩阵每个元素的平方和后开平方，注：Frobenius范数满足相容性

矩阵范数 - 知乎前面已经学习了向量范数，了解了向量范数的定义和性质，以及常见的几种向量范数。这一节将继续学习矩阵范数1. 矩阵范数的定义若函数 f : R^{ n×n} → R 满足 正定性：f(A) ≥ 0, ∀ A ∈ R^{n×n}， 等号当且仅当…https://zhuanlan.zhihu.com/p/370466759?utm_id=0

向量范数 - 知乎1. 写在前面这块内容如果只看书和PPT的话学起来会比较困难，因此在网上找了湘潭大学数值分析的课程学习这块内容，老师带着地域特色的普通话讲解很是可爱，定理的证明也很清晰。主要看这两节内容就行了，传送门如下…https://zhuanlan.zhihu.com/p/364624554