Sklearn中与特征缩放有关的五个函数和类，全部位于sklearn.preprocessing包内。作为一个系列文章，我们将逐一讲解Sklearn中提供的标准化和归一化方法，以下是本系列已发布的文章列表：

• Sklearn标准化和归一化方法汇总(1)：标准化 / 标准差归一化 / Z-Score归一化
• Sklearn标准化和归一化方法汇总(2)：Min-Max归一化

以下是Sklearn中的五种与特征缩放相关的函数和类，我们的研究也是为围绕这些函数和类展开的：

名称	方法名	类名
标准化 / Z-Score 归一化 / 标准差归一化	sklearn.preprocessing.scale	sklearn.preprocessing.StandardScaler
Min-Max 归一化	sklearn.preprocessing.minmax_scale	sklearn.preprocessing.MinMaxScaler
范数归一化	sklearn.preprocessing.normalize	sklearn.preprocessing.Normalizer
Robust Scaler（无常用别名）	sklearn.preprocessing.robust_scale	sklearn.preprocessing.RobustScaler
Power Transformer （无常用别名）	sklearn.preprocessing.power_transform	sklearn.preprocessing.PowerTransformer

关于各种关于标准化和归一化的概念和分类，我们已经在此前一篇文章《标准化和归一化概念澄清与梳理》中做了详细的梳理和澄清，不清楚的读者可以先阅读一下此文。本文我们研究第二种归一化手段：Min-Max归一化。本文地址：https://laurence.blog.csdn.net/article/details/128714596，转载请注明出处！

1. 算法

Min-Max归一化的算法是：先找出数据集通常是一列数据）的最大值和最小值，然后所有元素先减去最小值，再除以最大值和最小值的差，结果就是归一化后的数据了。经Min-Max归一化后，数据集整体将会平移到[0,1]的区间内，数据分布不变。计算公式如下：

$$x^{{}^{\prime }}=\frac{x-min(x)}{max(x)-min(x)}$$

2. 示例

在下面的示例中，我们准备了一组身高数据，这组数据符合以170为均值，170*0.15为标准差的正态分布。我们会通过三种方法计算出标准差归一化后的数据，从中我们可以理解Min-Max归一化的计算逻辑并掌握直接进行Min-Max归一的工具方法和类，以下是示例将要演示的3种计算方法：

1. 根据公式手动计算
2. 使用sklearn.preprocessing.minmax_scale直接处理
3. 使用sklearn.preprocessing.MinMaxScaler直接处理

以下是示例代码：

# Min-Max归一化

import numpy as np
import matplotlib.pyplot as plt
from sklearn.preprocessing import minmax_scale
from sklearn.preprocessing import MinMaxScaler
# author: https://laurence.blog.csdn.net/

%matplotlib inline
np.random.seed(42)
fig, (ax1, ax2, ax3, ax4) = plt.subplots(1, 4, figsize=(12,5))

heights = np.random.normal(loc=170, scale=170*0.15, size=1000)

print("1. 原始数据")
print(f"heights (first 3 elements) = {heights[:3]}")
print(f"heights min = {heights.min()}")
print(f"heights max = {heights.max()}")

ax1.hist(heights, bins=50)
ax1.set_title("raw data")
ax1.annotate(f"σ = {heights.std()}", (0.5, 0.95), xycoords='axes fraction', va='center', ha='center')

print("--------------------------------------------------------------------------------------------------------------")

print("2. 根据公式手动进行Min-Max归一化")
minmax_scaled_heights = (heights - heights.min()) / (heights.max() - heights.min())
print(f"minmax_scaled_heights (first 3 elements) = {minmax_scaled_heights[:3]}")
print(f"minmax_scaled_heights standard deviation = {minmax_scaled_heights.std()}")

ax2.hist(minmax_scaled_heights, bins=50)
ax2.set_title("manually scaled")
ax2.annotate(f"σ = {minmax_scaled_heights.std()}", (0.5, 0.95), xycoords='axes fraction', va='center', ha='center')

print("--------------------------------------------------------------------------------------------------------------")

print("3. 使用minmax_scale函数进行Min-Max归一化")
minmax_scaled_heights = minmax_scale(heights)
print(f"minmax_scaled_heights (first 3 elements) = {minmax_scaled_heights[:3]}")
print(f"minmax_scaled_heights standard deviation = {minmax_scaled_heights.std()}")

ax3.hist(minmax_scaled_heights, bins=50)
ax3.set_title("minmax_scale()")
ax3.annotate(f"σ = {minmax_scaled_heights.std()}", (0.5, 0.95), xycoords='axes fraction', va='center', ha='center')

print("--------------------------------------------------------------------------------------------------------------")

print("4. 使用MinMaxScaler函数进行Min-Max归一化")

# 在交付给Scaler前，需将一维数据转置为二维单列数组，以便适配Scaler接受的二维数组结构和轴向，即：按列进行缩放（axis=0)
# 受上层Transformer接口的约束，所有Scaler均不接受axis参数，默认按列计算，如要不想或不便转换，可以使用scale(axis=)函数进行缩放
heights = heights.reshape(-1,1)

minmax_scaled_heights = MinMaxScaler().fit_transform(heights)
print(f"minmax_scaled_heights (first 3 elements) = {minmax_scaled_heights[:3].tolist()}")
print(f"minmax_scaled_heights standard deviation = {minmax_scaled_heights.std()}")

ax4.hist(minmax_scaled_heights, bins=50)
ax4.set_title("MinMaxScaler")
ax4.annotate(f"σ = {minmax_scaled_heights.std()}", (0.5, 0.95), xycoords='axes fraction', va='center', ha='center')

plt.show()

输出数据：

1. 原始数据
heights (first 3 elements) = [182.6662109  166.47426032 186.51605772]
heights min = 87.34768282823865
heights max = 268.2446530116954
--------------------------------------------------------------------------------------------------------------
2. 根据公式手动进行Min-Max归一化
minmax_scaled_heights (first 3 elements) = [0.52692164 0.4374124  0.54820363]
minmax_scaled_heights standard deviation = 0.13796537483323715
--------------------------------------------------------------------------------------------------------------
3. 使用minmax_scale函数进行Min-Max归一化
minmax_scaled_heights (first 3 elements) = [0.52692164 0.4374124  0.54820363]
minmax_scaled_heights standard deviation = 0.13796537483323718
--------------------------------------------------------------------------------------------------------------
4. 使用MinMaxScaler函数进行Min-Max归一化
minmax_scaled_heights (first 3 elements) = [[0.5269216393004286], [0.43741239785083125], [0.5482036254822695]]
minmax_scaled_heights standard deviation = 0.13796537483323718

输出图表：

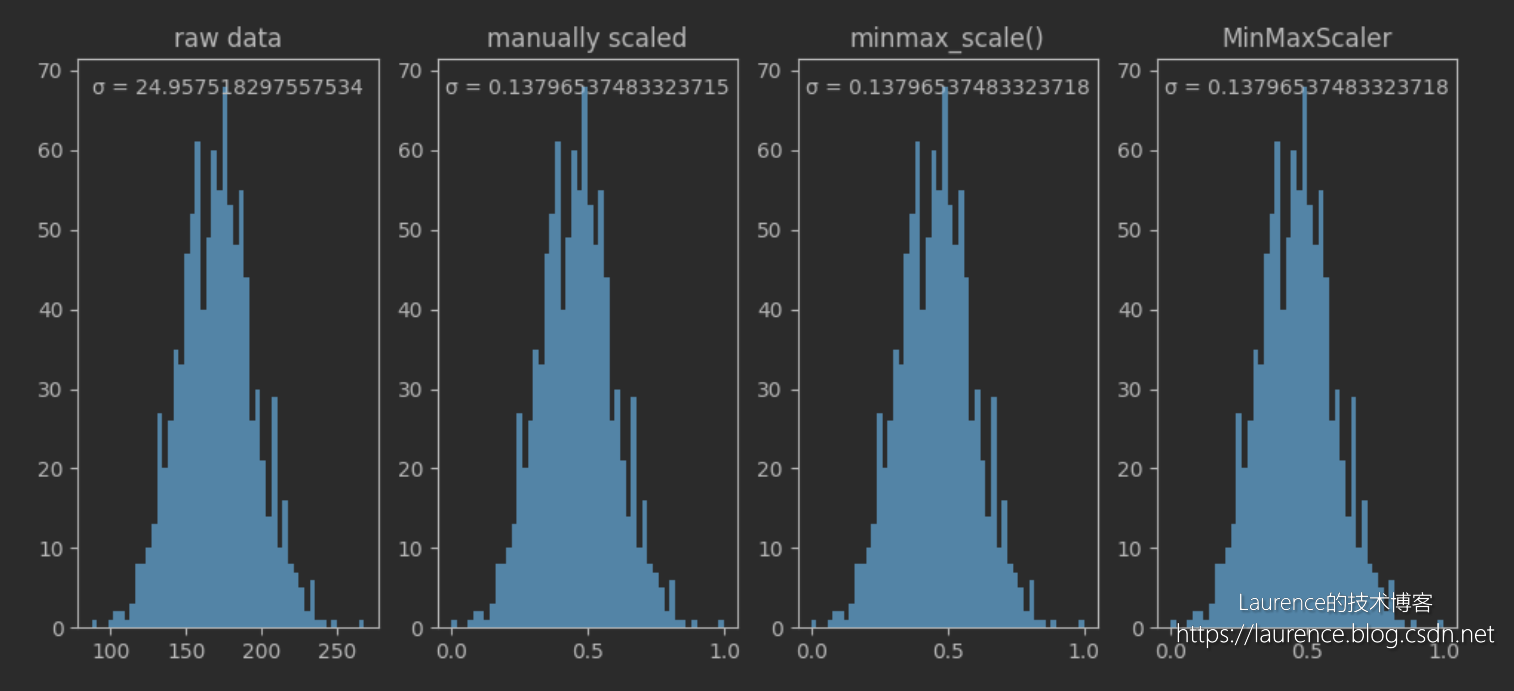
3. 解读

Min-Max归一化是所有特征缩放方法中最简单的，没有必要解读了，只是再提醒一下MinMaxScaler的使用方法：

sklearn.preprocessing包内的Scaler类均不接受一维数组，在将一维数组传给Scaler前，需将其转置为（只有一列的）二维数组；此外，受上层Transformer接口的约束，所有Scaler均不接受axis参数，默认按列计算，如要不想或不便转换，可以使用对应函数进行按行缩放（此类场景并不常见），对应函数有axis参数。