1 问题
在学习不同网络模型对实验精度的影响过程中,对我们的实验结果,各种参数数值的改变有何变化,有何不同。
VGG-11网络与LeNet-5网络对精度和损失的影响研究。
训练周期=20 其他参数都相同的方式来探索最终的精度。
其他参数都相同的方式来探索最终的精度。
2 方法
对于VGG-11网络,使用了八层卷积,五层池化,三层全连接,而LeNet网络,使用了两层卷积,两层池化,三层全连接。
新增的代码(网络模型,画图):
| ### VGG-11 class MyNet(nn.Module): def __init__(self) -> None: super().__init__() # 继承用法 self.conv1 = nn.Conv2d( in_channels=1, out_channels=6, stride=1, kernel_size=5, padding=0 ) self.avg_pool_1 = nn.AvgPool2d( stride=2, kernel_size=2 ) self.conv2 = nn.Conv2d( in_channels=6, out_channels=16, kernel_size=5, stride=1, padding=0 ) self.avg_pool_2 = nn.AvgPool2d( kernel_size=2, stride=2 ) self.fc1 = nn.Linear(in_features=16*4*4,out_features=120) self.fc2 = nn.Linear(in_features=120,out_features=84) self.fc3 = nn.Linear(in_features=84,out_features=10) def forward(self,x): x = self.conv1(x) x = self.avg_pool_1(x) x = self.conv2(x) x = self.avg_pool_2(x) # 此时格式为 [-,5,5,16] # 卷积后必须flatten 才能全连接,经过flatten x = torch.flatten(x,1) # [B,C,H,W] --> [-,C,H,W] x = self.fc1(x) x = self.fc2(x) out = self.fc3(x) return out ### LeNet-5 class MyNet(nn.Module): def __init__(self) -> None: super().__init__() # 继承用法 self.conv1 = nn.Conv2d( in_channels=1, out_channels=6, stride=1, kernel_size=5, padding=0 ) self.avg_pool_1 = nn.AvgPool2d( stride=2, kernel_size=2 ) self.conv2 = nn.Conv2d( in_channels=6, out_channels=16, kernel_size=5, stride=1, padding=0 ) self.avg_pool_2 = nn.AvgPool2d( kernel_size=2, stride=2 ) self.fc1 = nn.Linear(in_features=16*4*4,out_features=120) self.fc2 = nn.Linear(in_features=120,out_features=84) self.fc3 = nn.Linear(in_features=84,out_features=10) def forward(self,x): x = self.conv1(x) x = self.avg_pool_1(x) x = self.conv2(x) x = self.avg_pool_2(x) # 此时格式为 [-,5,5,16] # 卷积后必须flatten 才能全连接,经过flatten x = torch.flatten(x,1) # [B,C,H,W] --> [-,C,H,W] x = self.fc1(x) x = self.fc2(x) out = self.fc3(x) return out |
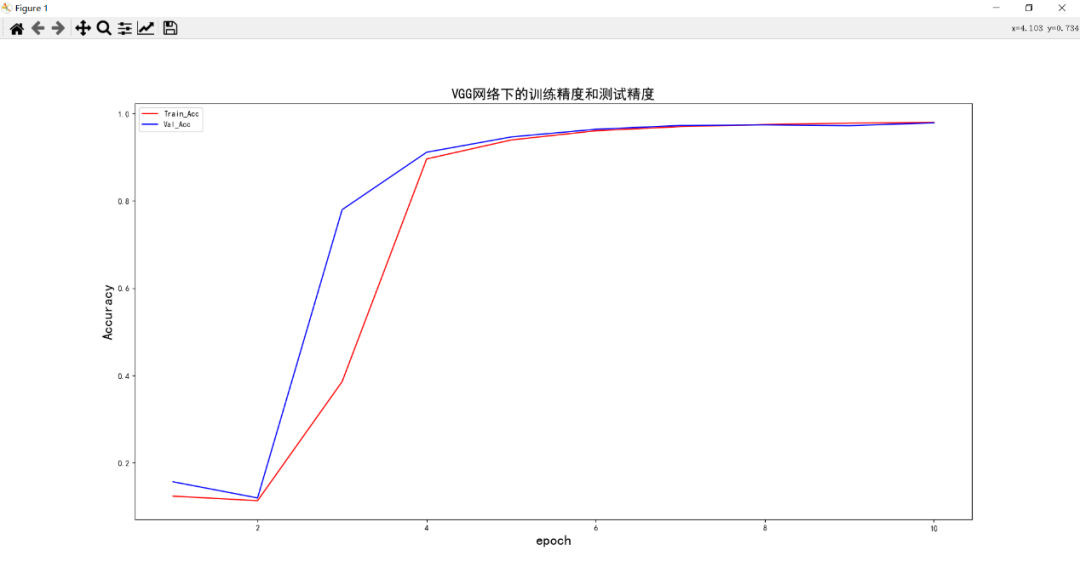
VGG-11网络:

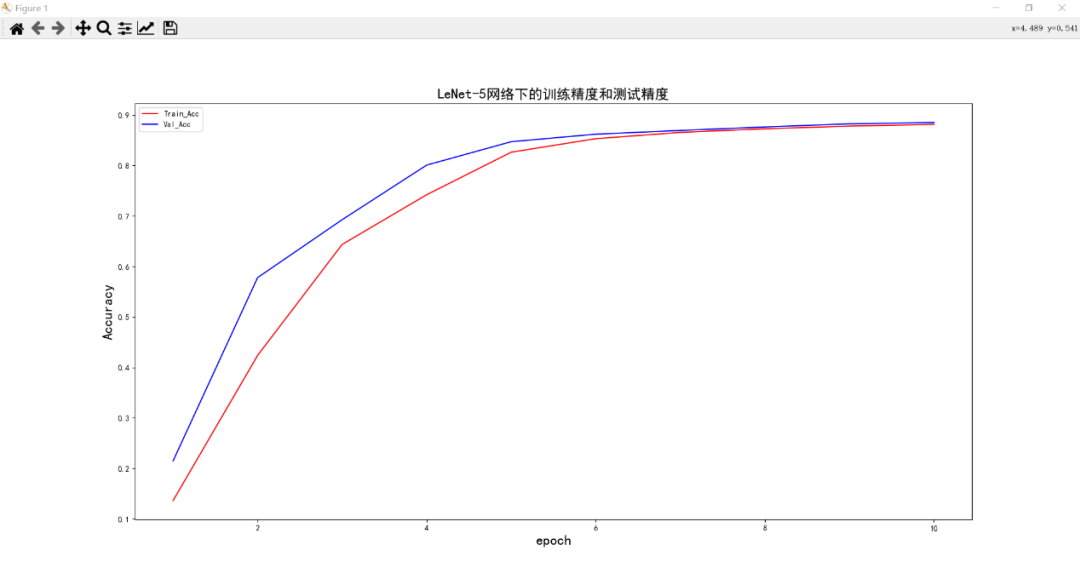
LeNet-5网络:

3 结语
根据最后的可视化展示图可以清晰地看到:
- VGG-11网络在十次周期的训练下,训练精度和验证精度虽第二次较第一次精度还下降了,但从第二次周期起到第六周期精度的提升较大,精度差不多在95%左右,后面的几次周期虽然也在提升精度,但提升的幅度不是很大.
LeNet-5网络在十次周期的训练下,训练精度和验证精度,训练周期次数与精度成正比,且在前七次的周期下,精度提升较快,后面三次的训练,提升幅度较小 - 根据最终的实验结果可以看到,两个网络模型都是在训练十次的时候精度最高,LeNet-5测试精度为89.04% ; VGG-11测试精度为98.15%,可见VGG-11网络的效果较好
- 虽然二者的精度相差有点大,但是LeNet-5的训练时间较VGG-11的训练时间较少,但除了时间问题上,VGG-11网络比LeNet网络要好。
最后不足:1、本次实验的训练次数只有十次,精度最高的Epoch都为10,所以不知道再训练100、1000次后的精度是怎么改变,精度最高的epoch也不知。
2、在实验最初开始前,没统计网络模型的训练时间,后面也无法根据训练时间这一指标来比较这两模型的好坏。

![Python【r e】模块正则表达式[中]实战](https://img-blog.csdnimg.cn/img_convert/98f33575fd1b305db60516c806d8f792.png)