这节的内容主要讲述在关节空间和任务空间中的运动控制中的反馈控制，力控制，运动-力混合控制以及阻抗控制、导纳控制，pid控制等内容。

在之前的内容当中，往往不涉及到实际对机器人的操纵，即我们计算出一个结果，就默认机器人可以执行这个期望的指令，而没有考虑到机器实际上是存在误差的，它实际执行的结果很可能不是我们所期望的命令，因此引入了本章的控制部分内容。

为了避免简单的抄书，本节我只整理一些我认为的重点内容。这节的内容也是较多的，但也是日常机器人工程中非常经典的一些理论内容。

---

误差动力学

• 稳态误差：令θ为期望的位置与实际位置的差值，即“误差”，稳态误差为当时间t趋近于无穷时的误差。

• 超调：即误差的最低点到稳态误差的距离，除以0时刻到稳态误差的距离，求绝对值并用百分比表示。

• %2调节时间：实时误差到稳态误差的距离，在第一次到达初始时刻的%2这一条件的时间。

• 稳态响应：通过稳态误差表征。

• 瞬态响应：通过超调和%2调节时间来表征。

线性误差动力学

用p阶微分方程来表示误差：

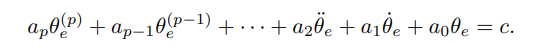
这里采用高等数学上册微分方程一节的内容，求解特征多项式：

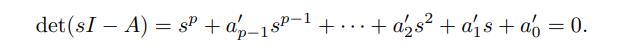
求s这个复数。如果这个方程的每个根s都有负实部，则误差动力学稳定。反之如果有任何一个根存在正实部，误差动力学不稳定，误差会随着时间趋近于无穷，无限制的增长。

一阶误差动力学和二阶误差动力学

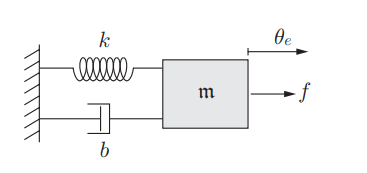
质量-弹簧 -阻尼系统，其中阻尼相当于“避震”，作用于速度项，可以与弹簧配合使用，从而避免弹簧来回震荡。弹簧会发生形变，而阻尼则阻碍物体向某一方向施加运动。

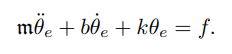
上文则为质量块的运动方程，k是弹簧常数（即刚度），b为阻尼，m为质量，f为外力。

如果质量块趋近于0，则二阶动力学降阶为一阶动力学，并认为外力产生速度而非加速度。

这部分的内容比较考验读者对高等数学的回忆，呵呵，对很多学生而言，当时学高等数学的时候，许多概念不知道有什么用。但是现在知道有什么用了，却忘记当时怎么讲的了！这里只写结论了：

一阶误差动力学：

当外力为0的时候:

注意，两个t是不一样的，斜体t表示时间，正体t=b/k，称为“时间常数”，表示一阶指数衰减到初始值37%大小所对应的时间。而2%调节时间约为4t左右。

弹簧常数k增大，阻尼常数b减小，响应变快。

二阶误差动力学：

首先把质量除以到后两项上：

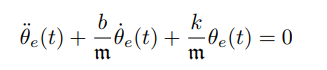
然后依旧是求解特征多项式：

w为自然频率，

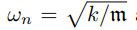
而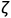作为阻尼比，

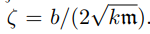
特征多项式的结果是：

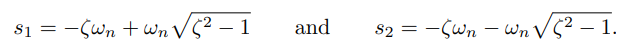
如之前所说，为了使该方程误差稳定，两个根要有负实部。即k和b都要大于0才能做到。

接下来就引入了控制学科非常重要的概念：

根s1和s2是：
不等的两个实数， ，称为过阻尼。
相同的两个实数， ，称为临界阻尼。
共轭复数， ,称为欠阻尼。

对于过阻尼（Overdamped ），方程的解为：

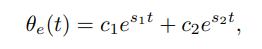
即送入时间，就可以得到此时的误差。因为它是实数，所以不存在虚部，它的根在实轴和虚轴上分布为：

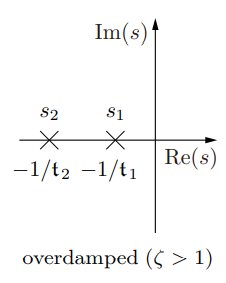
这两个解，越往左走，调节时间越短。时间常数t为1/s1。

当临界阻尼（critically damped ）的时候，两个根s重合了：

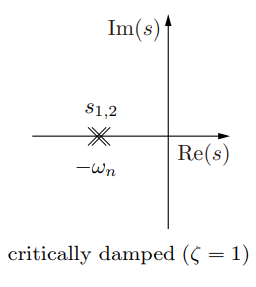
这时候方程的解为：

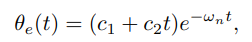
其实这种情况下误差减小是最好的，既快，又没有超调。

时间常数t为：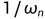

对于临界阻尼（Underdamped）而言，它是一对共轭复数，越往虚部两边走，超调和振荡增大。

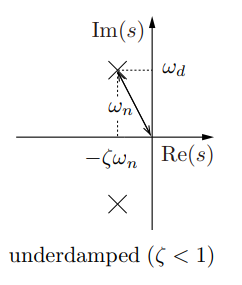
时间常数t为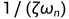

即三种阻尼比的表现结果：

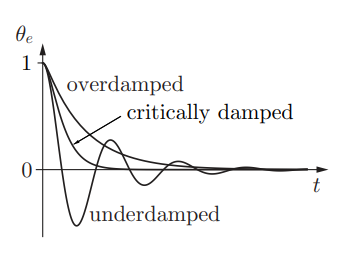
1.不管哪种情况，只要误差动力学稳定，%2时间常数为4t。
2.对于欠阻尼的超调情况，这里记录一下：阻尼比 =0.1，超调为73%，阻尼比为0.5时，超调为16%，阻尼比为0.1时，超调为1.5%。
3.记忆各种阻尼情况，只需要理解阻尼是起到阻碍作用，如果是过阻尼，就相当于阻力太大了，因此误差下降的慢。而欠阻尼则是缺少阻尼，因此误差存在来回振荡的情况。

速度输入的运动控制

本部分开始逐步接触控制学中最经典的pid控制，并深入的讲解了各部分的作用，是一个比较好的入门资料。不过本部分的前提是，控制量为“速度”。

单关节的运动控制

本部分分为 前馈控制、反馈控制 以及 前馈+反馈控制。

前馈控制其实就是开环控制，直接发期望的速度，也不管机器人到底执行到位没有。

反馈控制的思路则是根据实时的反馈，进行一个弥补，差多少，补多少。即直接根据位置误差得到控制量，和前馈控制不同，并不在乎各个时刻的期望速度到底是多少。

p控制和一阶误差动力学

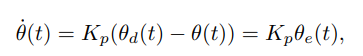
对于期望位置恒定，期望速度为0的情况，即最简单的控制问题，要求机器人保持在某个位置不动，称之为“设定点控制”，像这种控制问题，p控制则已经足够。误差越大，指令速度则越大，误差越小，指令速度则越小。这种情况下的时间常数t为1/Kp，同样2%调节时间为4t。kp越大，响应越快。也没有稳态误差，机器人总归能达到误差为0的地步。

而对于期望位置非常数，期望速度为常数的情况，相当于机器人的期望位置以恒定的速度变化，，那么直观上感觉，基于反馈控制的p控制似乎有点跟不上。这个用求解的方式也可以证明，当时间无限大的情况下，解会收敛到c/Kp，c为速度。那么如果用p控制，为了减少这个c/Kp的稳态误差，我似乎可以一直增大Kp，这样分母增大，稳态误差就变小了。但这会导致两个问题：1.关节速度是有最大限制的，并不是你想给多大就给多大。2.控制器为离散时间，Kp较大可能导致控制不稳定，比如无法精确落在某点。

pi控制和二阶误差动力学

为了针对上面的问题，引入了pi控制，多了一个积分项。

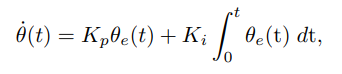
积分项的引入恰恰就是为了解决这个稳态误差。当Ki，Kp都大于0时，这个二阶误差动力学是稳定的。Ki增大，响应也会变快，因为Ki考虑到了误差的累计值，并且进行及时的弥补。

在上文二阶误差动力学中提到的固有频率和阻尼比：

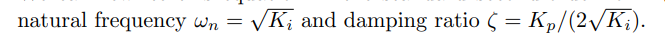
我们可以看到，增大Ki，阻尼比变小，响应变快。在临界阻尼的情况下，效果最好。继续增大，变成了欠阻尼，则系统开始振荡和超调。

所以PI控制的选择原则是，利用临界阻尼，得到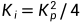，选择合适的Kp和Ki，并根据实际的机器人情况去增大它，从而生成任意的快速响应。

对于期望速度是常数的情况，PI控制可以消除稳态误差。

但是对于期望速度不是常数的情况下，Pi控制不能消除稳态误差。

对于前馈+反馈控制，则公式变为：

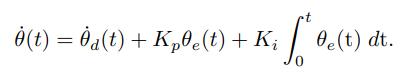
这玩意乍一看，似乎和前面的PI控制有些矛盾。不过这里其实已经换了一种思维了。即Kp和Ki两项之和，已经不再作为控制量。现实其实一般都是用的前馈+反馈控制。

也就是说：反馈控制是，位置误差为0，则控制它的速度为0。而前馈+反馈控制，位置误差为0，则直接用期望速度当作是控制速度。因此前馈+反馈的控制方法可以弥补反馈控制的滞后性（它必须基于一个误差才能开始控制环节，似乎永远慢一拍）。

多关节的运动控制

和单关节运动控制类似，只不过使用矩阵形式的Kp和KI罢了。

任务空间的运动控制

刚刚讲的都是控制的是关节空间的内容，即我就控制一个关节角度。但是对于控制任务空间，例如笛卡尔空间末端控制，它不再是控制关节角了，怎么办呢？

这其实就跟应用题一样，套入一个任务空间的控制量就可以了，我就不细说了，相信大家都能看懂。

唯一需要注意的是，有两种控制方式，一种是控制末端旋量：

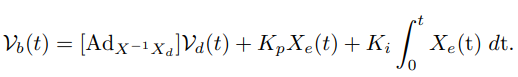
其中d是期望的末端旋量，b是真正控制的末端旋量。利用旋量来控制，旋转和平移不是解耦的，即走出的是一条弧线：

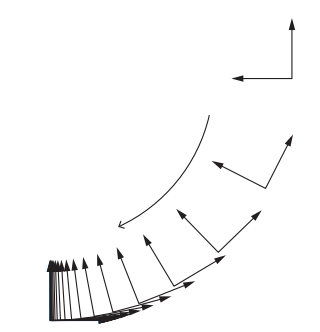
但如果根据另一种方式进行解耦：

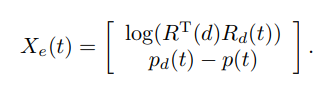
那要是这样的话，旋转和平移就成功实现了解耦：

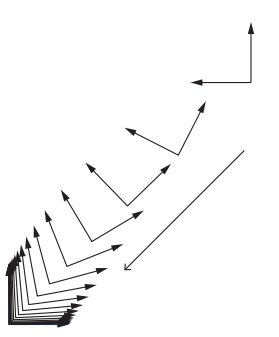
力或力矩输入的运动控制

单个关节的运动控制

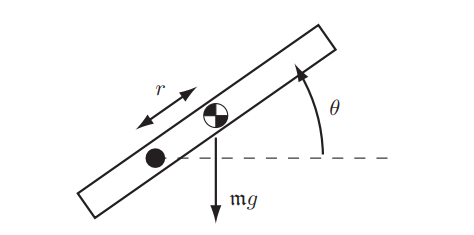
这里它放了一个图，想先分析单个刚体的动力学模型。

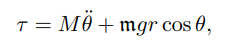
有的同学可能有些好奇这个公式是怎么得到的。

第一项呢，中文版书176页其实已经提到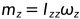，，参见：【现代机器人学】学习笔记七：开链动力学（前向动力学Forward dynamics 与逆动力学Inverse dynamics），第二项则可以理解为 力 叉乘 力臂，因为r是从质心到转轴的距离。

旋转摩擦主要是由粘性摩擦引起（回顾：粘性摩擦的摩擦力矩随着速度的增加而增加），因此在公式中再增加一个摩擦的力矩：

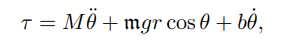
那么这就变成了一个包含位置、速度、加速度的二阶动力学方程。

那么这节依旧是：前馈控制、反馈控制、前馈+反馈控制。

反馈控制：

PID控制简介：

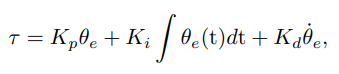
可以看到，相比前述介绍的PI控制，这里新增了一个和误差的时间导数有关的微分项。

综合整理一下：比例增益Kp，试图减小位置误差的一个虚拟弹簧；而积分增益Ki，试图减少或消除稳态误差。而新增的这个微分增益Kd，类似一个试图减小速度误差的虚拟阻尼。

我们知道,Ki取得太大，会导致超调，而取小不能完全消除稳态误差。

Kd会对偏差变化提前预报，取大可以使得响应更快，减少超调。但Kd也不能太大，因为这会使得系统提前制动，从而延长了调节时间。

PD控制与二阶误差动力学

我们先假设不要Ki这一项，我们是希望能快速响应，因为积分项i可能会导致超调和不稳定。有时候我们不在乎一点点的误差，而是希望机器人比较稳定，这时候pd控制就派上了用场。（例如定点控制其实也不需要积分项，因为pi控制适用于那些位置变化、速度为常数的场合）

依旧是使用前面类似的方法，不过得到的阻尼比和固有自然频率为：

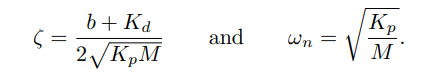
为了误差稳定，我们要求b+kd和kp必须为正。和上述pi控制类似，可以根据这个阻尼比，选择kd和kp，让它尽可能的满足临界阻尼。

PID控制与三阶误差动力学

这里发现一件很有趣的事情，就是刚刚的动力学方程：

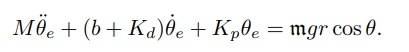
如果仅使用pd控制，那么就只有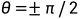的时候，才可以精准控制，因为这个时候等式右侧为0。

而等式右侧不为0的时候，即期望有一个角度，而左侧反馈控制又是根据误差θe来控制的，这就形成了一对矛盾，即控制的准，误差为0，则到不了右侧的期望θ，即误差也不可能是0。。。

那么这时候如果左侧加上一项积分项，那么就恰好满足了误差为0的时候等式左侧有一项非零项，刚好使得这个等式成立。

因此相比PD控制，误差稳定的条件为：

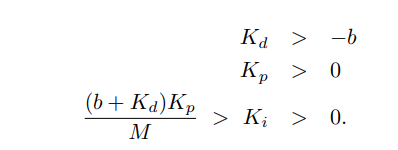
我们可以看到多了一个ki项的限制，而kd和kp则和pd控制一样。

所以设计策略为：先选择Kp和Kd，以获得良好的瞬态响应。然后再选择Ki，Ki要足够大从而减少或消除稳态误差，但是也不能太大，也要足够小，使其不会显著影响稳定性。

关于PID控制的流程，代码其实很简单，书里放了一个样例伪代码，一看就懂：

前馈控制：

根据机器人动力学模型主动产生力矩，而不是等待误差。

力的前馈控制其实比较依赖于动力学建模的稳定性。动力学建模我们一般采用rbdl等开源库来计算（当然不可能是完全手推造轮子了），参见：rbdl动力学库简单易用示例代码

但是如果建模不够精准，比如重力效应未建模，就是书中的图11.17所示的情况了，期望和相差会很远。实际上重力建模大家都能想到，动力学建模方面最难的就是对摩擦力进行建模，这个各个机器人都不一样，建模起来很麻烦。

前馈+反馈线性化

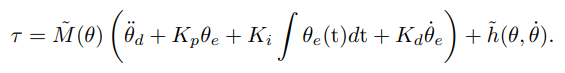
和上面一样，把前馈控制和反馈控制结合起来，就得到了这个公式。如果熟悉动力学公式和前面的PID控制的话，相信看这个公式会觉得很简单。

这个方程叫做“前馈加反馈线性化控制器”，“逆动力学控制器”，“计算力矩控制器”等名称。

“反馈线性化”是啥意思？即使用θ和θdot的反馈来生成线性误差动力学，而h消除了状态的非线性动力学部分。可以注意到上面的公式，其实本质上PID作用的是那个加速度项，而不是关节力矩。

我们看一看三种控制方式的不同：

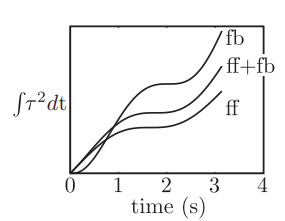
前馈+反馈比纯粹的前馈跟踪效果要好，而比纯粹的反馈控制更省力。

多关节的机器人运动控制

这一节主要掌握概念：即分散控制和集中控制。

分散控制其实指各个关节使用独立的控制器。这种情况适用于机器人各个关节的动力学解耦的时候（或者近似解耦），采用分散控制比较合适。如动力学一节所述，当各个关节的加速度仅仅取决于该关节的扭矩，位置和速度的时候，就是动力学解耦。（这种情况下，质量矩阵是对角阵）

集中控制：指集中式多关节控制。当重力和力矩比较显著和耦合的时候，或者质量矩阵无法用对角阵近似，则不得不使用集中控制。所以这种情况下，是类似前面速度输入的运动控制部分，从单关节扩展到多关节的时候，使用了对角阵来设定各个关节的pid系数，并且用整个误差向量来耦合到一起：

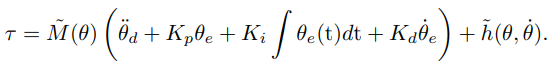
这个方程表面上和单关节部分的一致，实际上是不同的。主要是两点，第一，θe是误差向量；第二，Kp，Ki，Kd是增益矩阵，而不是一个单个的pid系数。

任务空间中的运动控制

既然是任务空间，实际上就是常见的笛卡尔空间末端控制了。有两种可能选项：

1. 第一种选项，根据逆运动学，把末端的位姿转换为关节位置，从而直接转为关节空间的运动控制。

2. 第二种选项，在任务空间表达机器人的动力学。即给定关节角，速度、末端执行器旋量，然后求末端执行器的力旋量 ，这是动力学那章的内容：

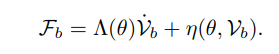
通过静力学公式，

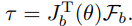
我们代入到之前得到的计算力矩控制律中，

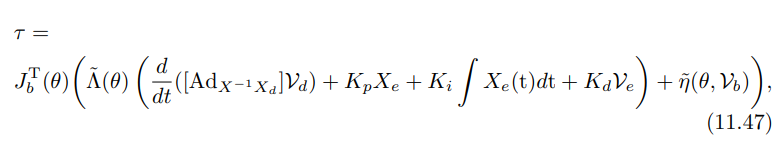
从而得到任务空间中的pid运动控制方法。

力控制

剩下的内容晚点再做补充，要睡觉了。。后续更新。