数模的主要比赛

美赛（报名费100美元，每年2月比赛）；国赛（每年9月）

电工杯（每年5月）；APMCM（每年11月）；MathorCup（每年4月）

 数模的一般步骤

      ①模型准备②模型假设③模型建立④模型求解⑤模型分析⑥模型检验

数模的基本流程

     Ⅰ.题目，摘要、关键词

     Ⅱ.问题重述，问题假设，问题分析

     Ⅲ.符号说明 

     Ⅳ.模型建立，模型求解，模型评价

     Ⅴ.参考文献

数模的应用工具

SPSSPRO

数模的赛题类型

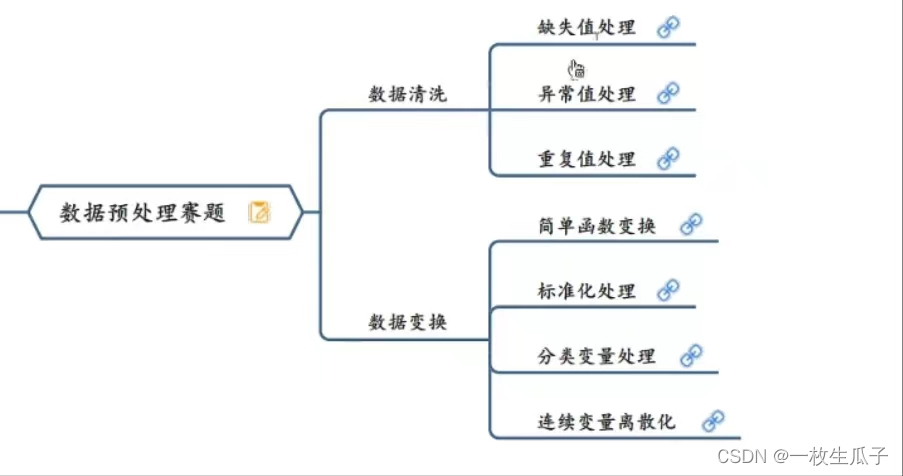
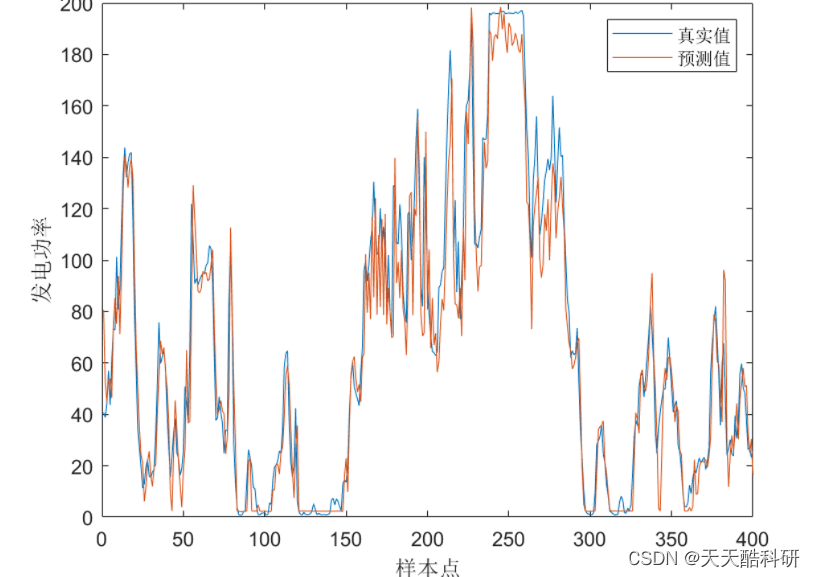
   一、预测类

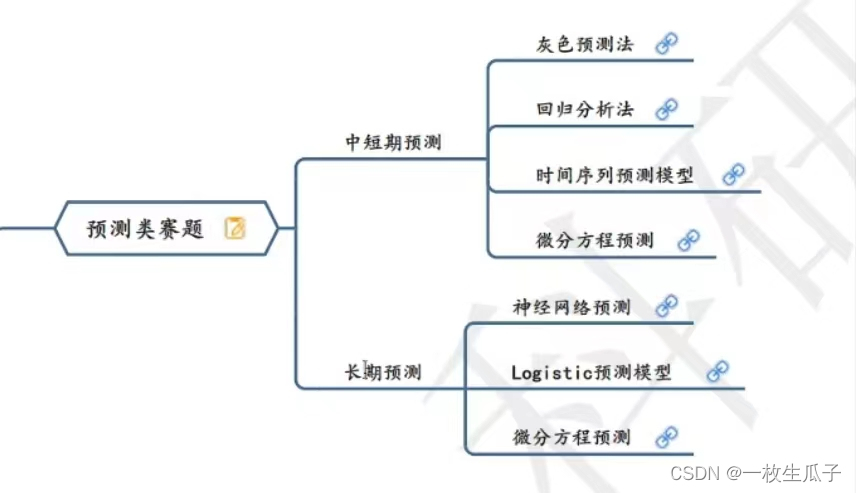
   二、评价类 

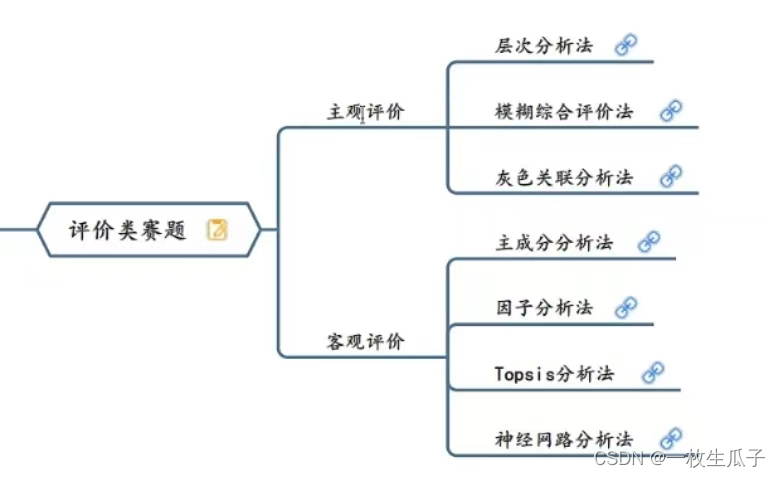
   三、机理分析类

   四、优化类

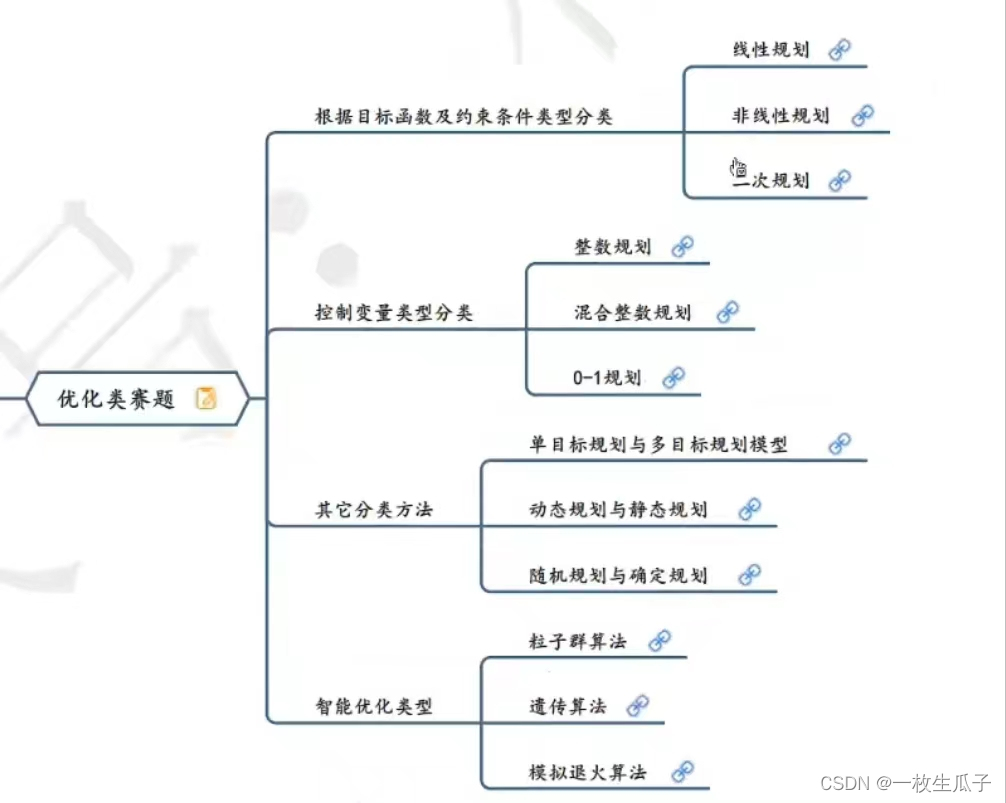
数模的团队分工

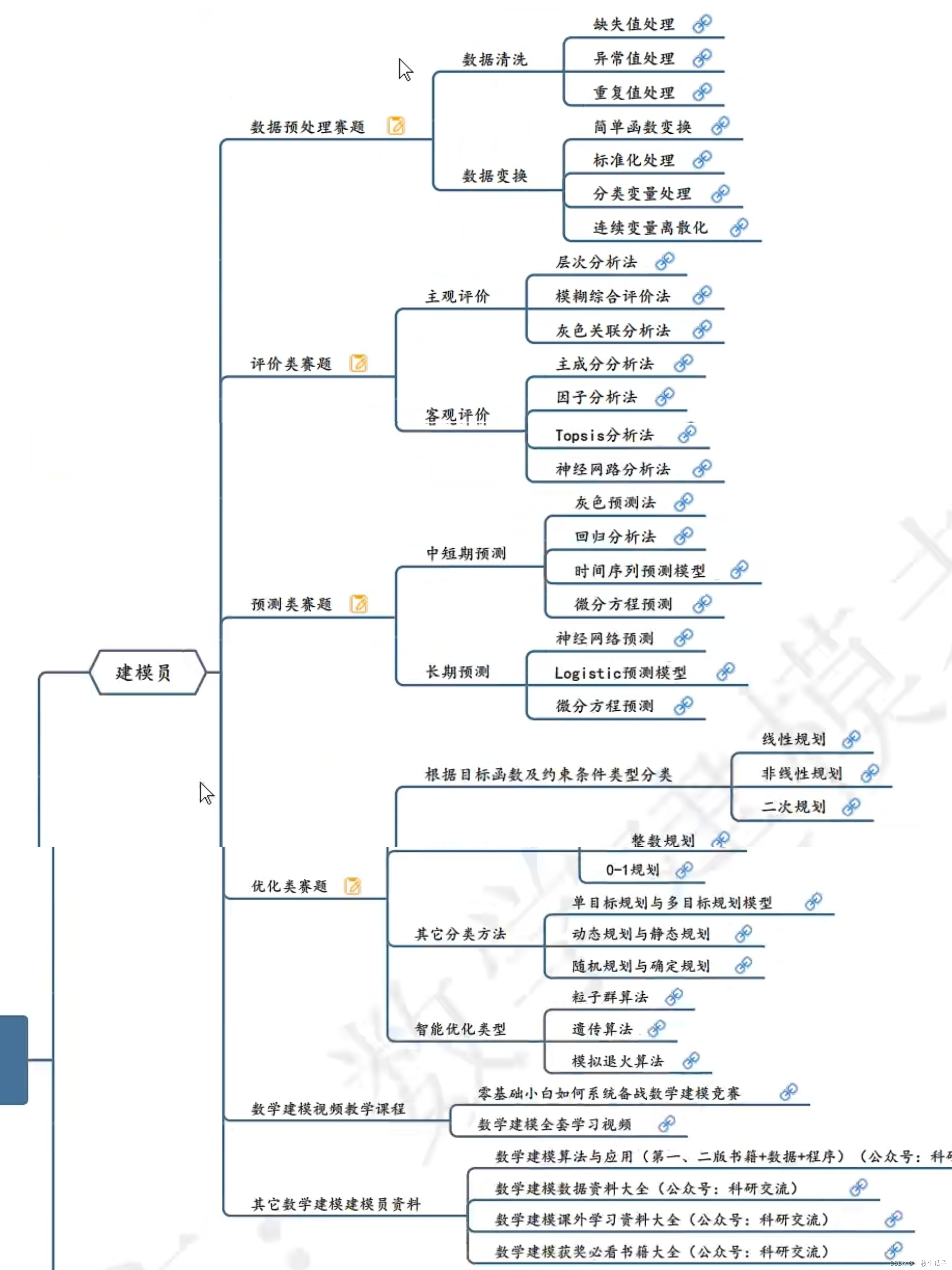
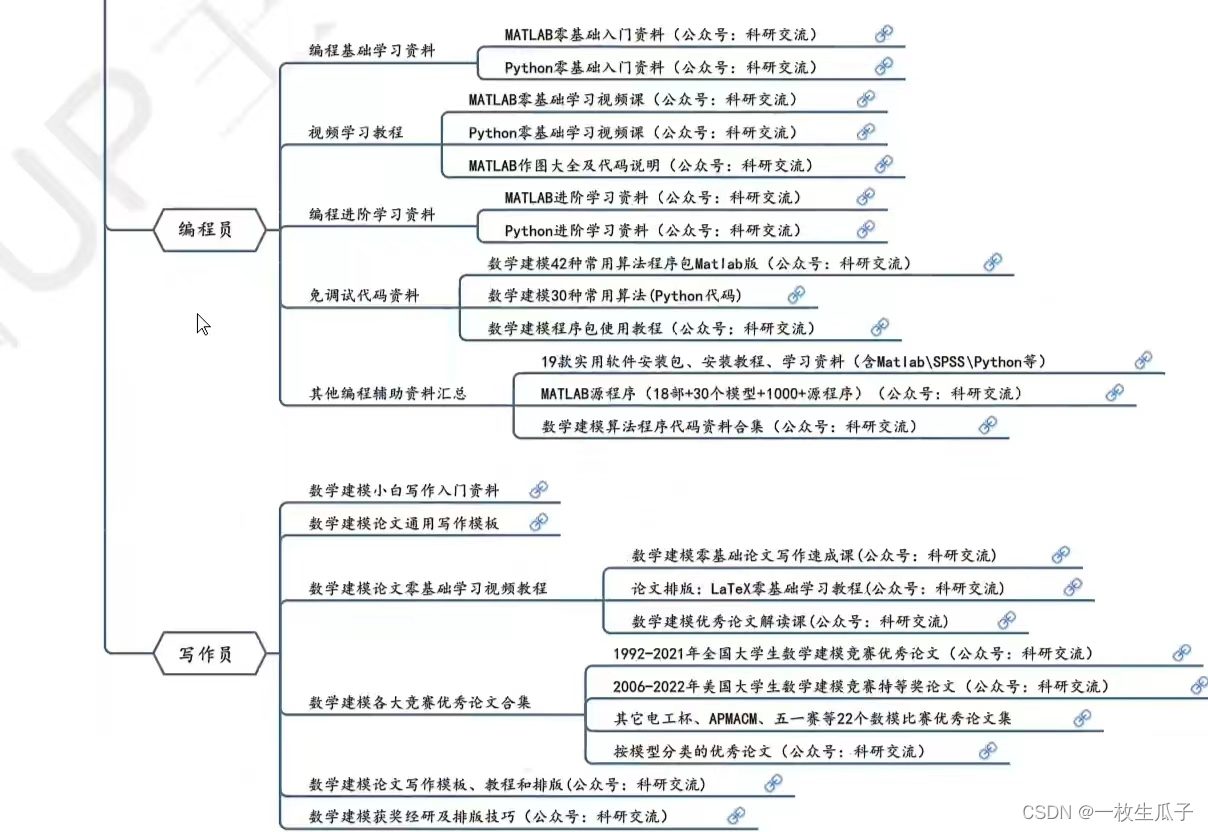
一、题目

基于———模型的————研究与分析

二、算法

   1.线性规划模型（LP）

   使用范围： 利用有限资源获取利益最大化（目标函数最值）

   使用条件：目标函数和约束条件必须均为线性函数

   需要决策变量、目标函数、限制条件三个关键必要部分（常用s.t.表述受约束的意思）

   可行解

        满足约束条件的解（可行域R'：所有可行解组成的集合）

   最优解

       同时达到目标函数需求的解

  灵敏度分析

       指对系统因周围条件变化显示出来的敏感程度的分析（即因现实因素导致常量起伏而对最优解的影响）

Matlab求解数学规划问题采用两种模式：①基于求解器的求解方法②基于问题的求解方法

线性规划的Matlab求解

当求最大值时，Matlab的标准型目标函数前加负号，限制条件左右两边加负号，并且改变符号方向