参考链接:https://hands1ml.apachecn.org/2/#_12
数据探索和可视化、发现规律
通过之前的工作,你只是快速查看了数据,对要处理的数据有了整体了解,现在的目标是更深的探索数据。
首先,保证你将测试集放在了一旁,只是研究训练集。
另外,如果训练集非常大,你可能需要再采样一个探索集,保证操作方便快速。
在这个案例中,因为数据集很小,所以可以在全集上直接工作。创建一个副本,以免损伤训练集
housing = strat_train_set.copy()
地理数据可视化
因为存在地理信息(纬度和经度),创建一个所有街区的散点图来数据可视化是一个不错的主意
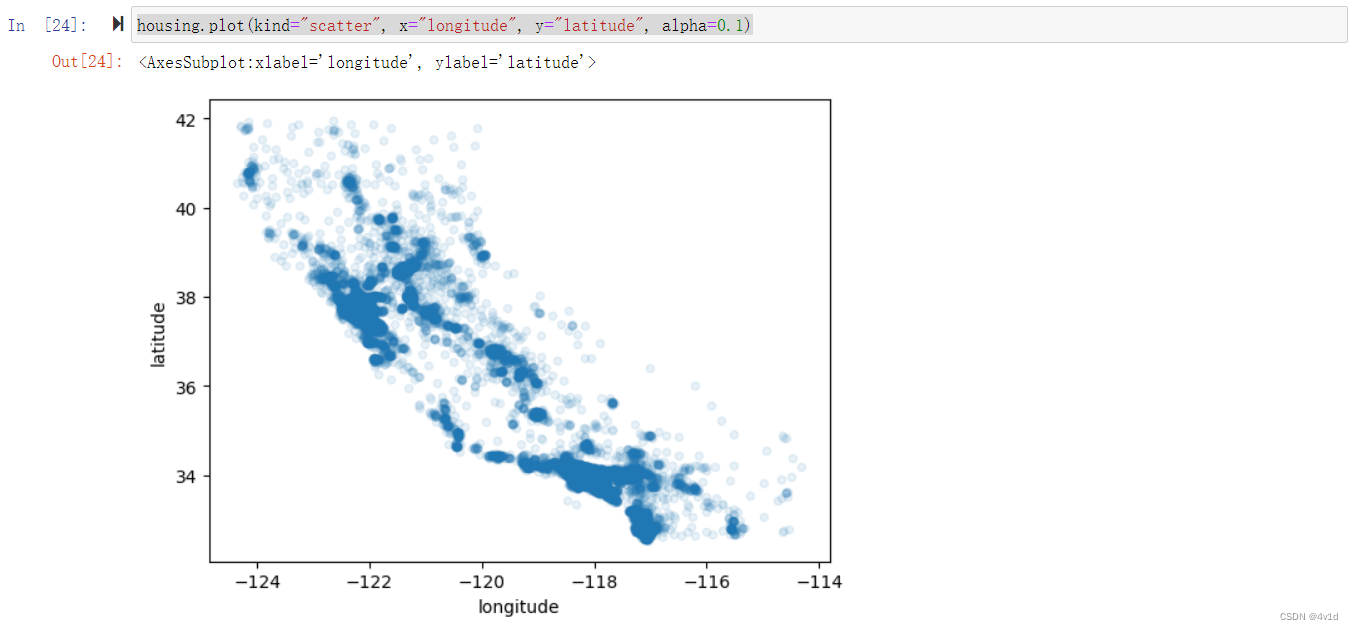
housing.plot(kind="scatter", x="longitude", y="latitude")
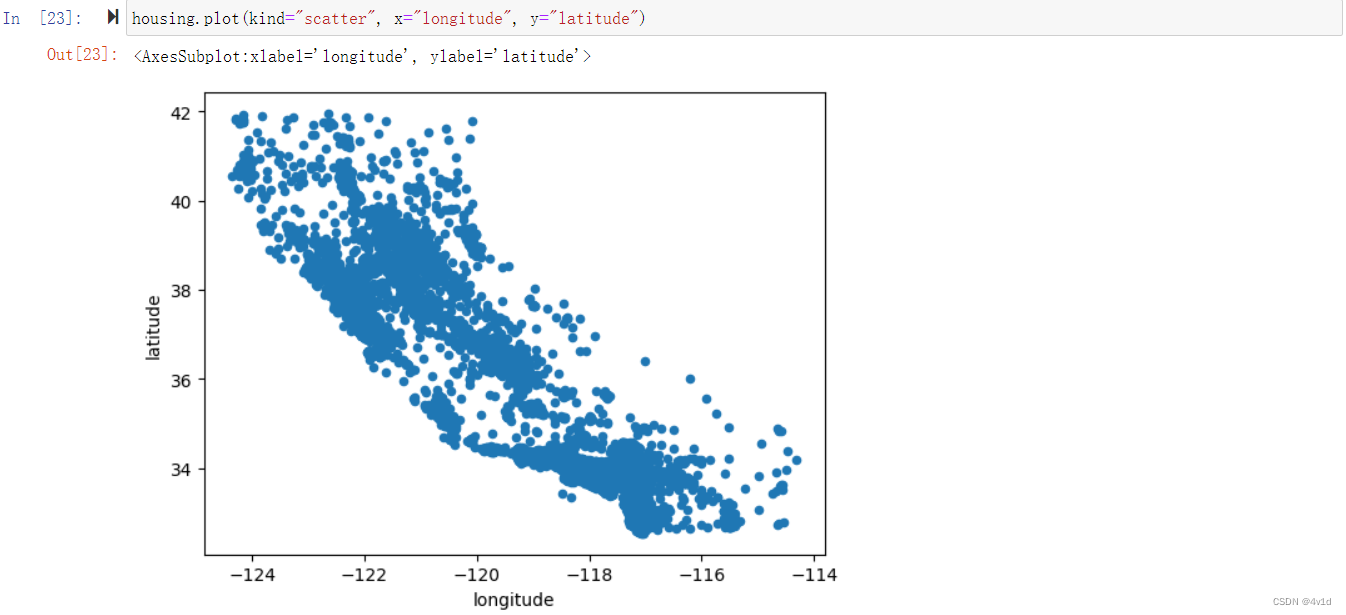
这张图看起来很像加州,但是看不出什么特别的规律。
可以将alpha设为 0.1,可以更容易看出数据点的密度 ,参数alpha设置了散点的透明度,通常用于显示密集程度。
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.1)
现在看起来好多了:可以非常清楚地看到高密度区域,湾区、洛杉矶和圣迭戈,以及中央谷,特别是从萨克拉门托和弗雷斯诺。
通常来讲,人类的大脑非常善于发现图片中的规律,但是需要调整可视化参数使规律显现出来。
现在将注意力转到房价上。
每个圈的半径表示街区的人口(选项s),颜色代表价格(选项c)。我们用预先定义的名为jet的颜色图(选项cmap),它的范围是从蓝色(低价)到红色(高价):
housing.plot(kind="scatter", x="longitude", y="latitude", alpha=0.4,
s=housing["population"]/100, label="population",
c="median_house_value", cmap=plt.get_cmap("jet"), colorbar=True,
)
plt.legend()
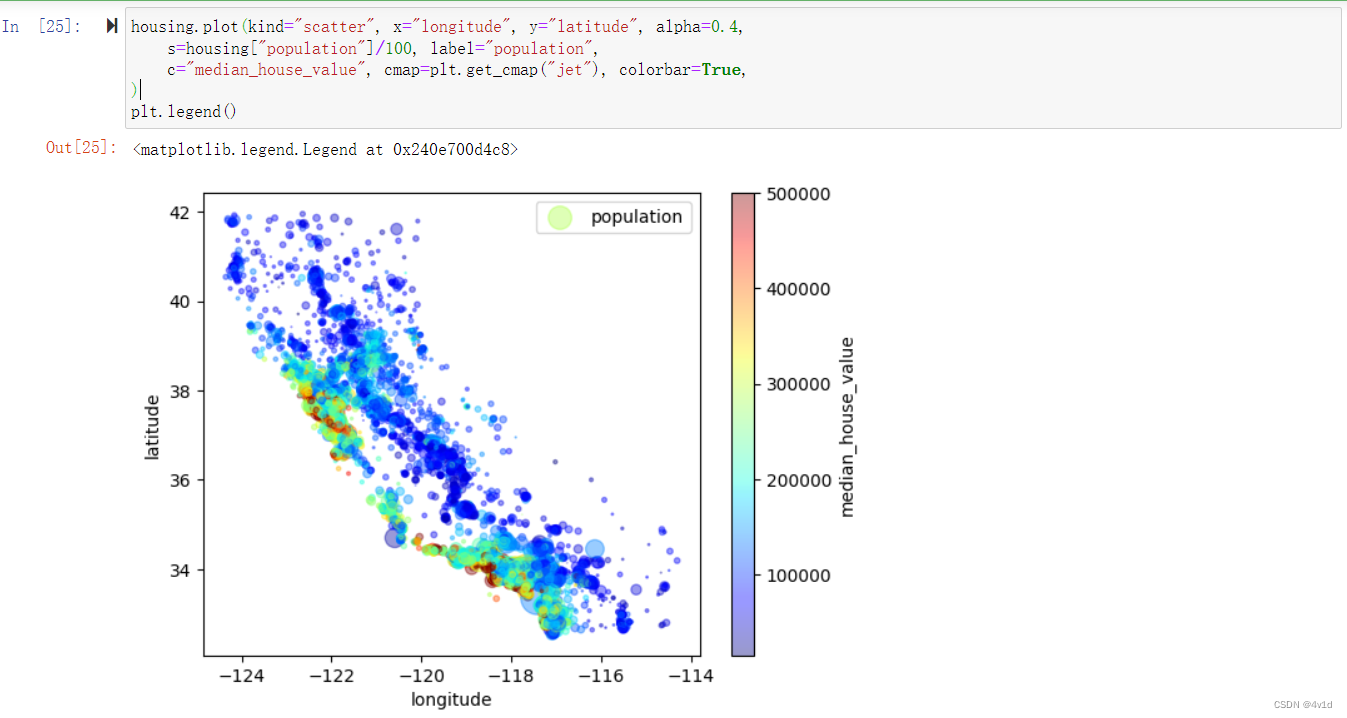
这张图说明房价和位置(比如,靠海)和人口密度联系密切,这点你可能早就知道。可以使用聚类算法来检测主要的聚集,用一个新的特征值测量聚集中心的距离。尽管北加州海岸区域的房价不是非常高,但离大海距离属性也可能很有用,所以这不是用一个简单的规则就可以定义的问题。
查找关联
因为数据集并不是非常大,你可以很容易地使用corr()方法计算出每对属性间的标准相关系数
(standard correlation coefficient,也称作皮尔逊相关系数)

corr_matrix = housing.corr()
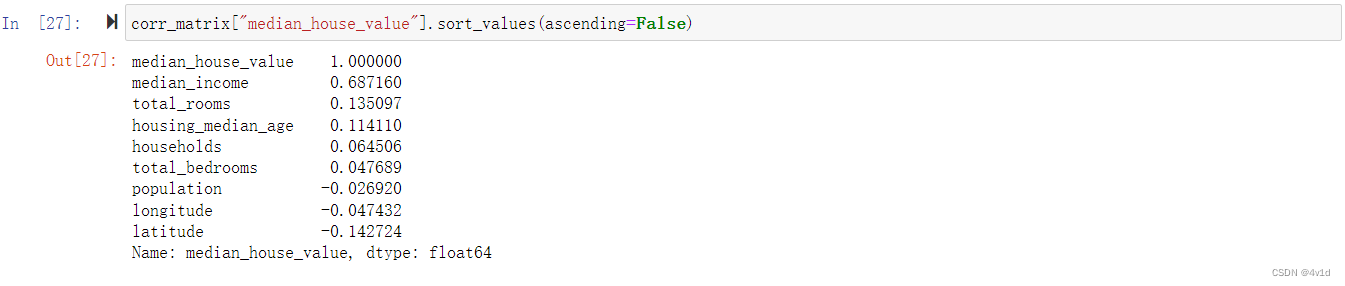
相关系数的范围是 -1 到 1。当接近 1 时,意味强正相关;例如,当收入中位数增加时,房价中位数也会增加。当相关系数接近 -1 时,意味强负相关;你可以看到,纬度和房价中位数有轻微的负相关性(即,越往北,房价越可能降低)。最后,相关系数接近 0,意味没有线性相关性。
另一种检测属性间相关系数的方法是使用 Pandas 的scatter_matrix函数,它能画出每个数值属性对每个其它数值属性的图。因为现在共有 11 个数值属性,你可以得到11 ** 2 = 121张图,在一页上画不下,所以只关注几个和房价中位数最有可能相关的属性
from pandas.plotting import scatter_matrix
attributes = ["median_house_value", "median_income", "total_rooms",
"housing_median_age"]
scatter_matrix(housing[attributes], figsize=(12, 8))
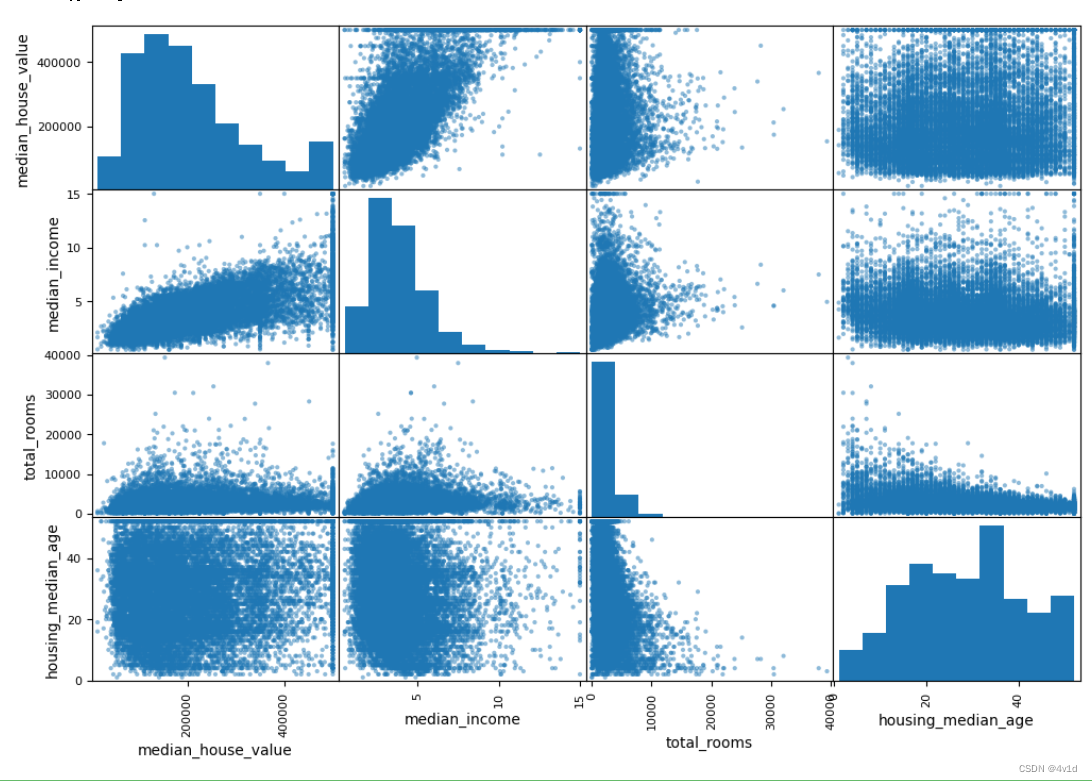
最有希望用来预测房价中位数的属性是收入中位数,因此将这张图放大
housing.plot(kind="scatter", x="median_income",y="median_house_value",
alpha=0.1)
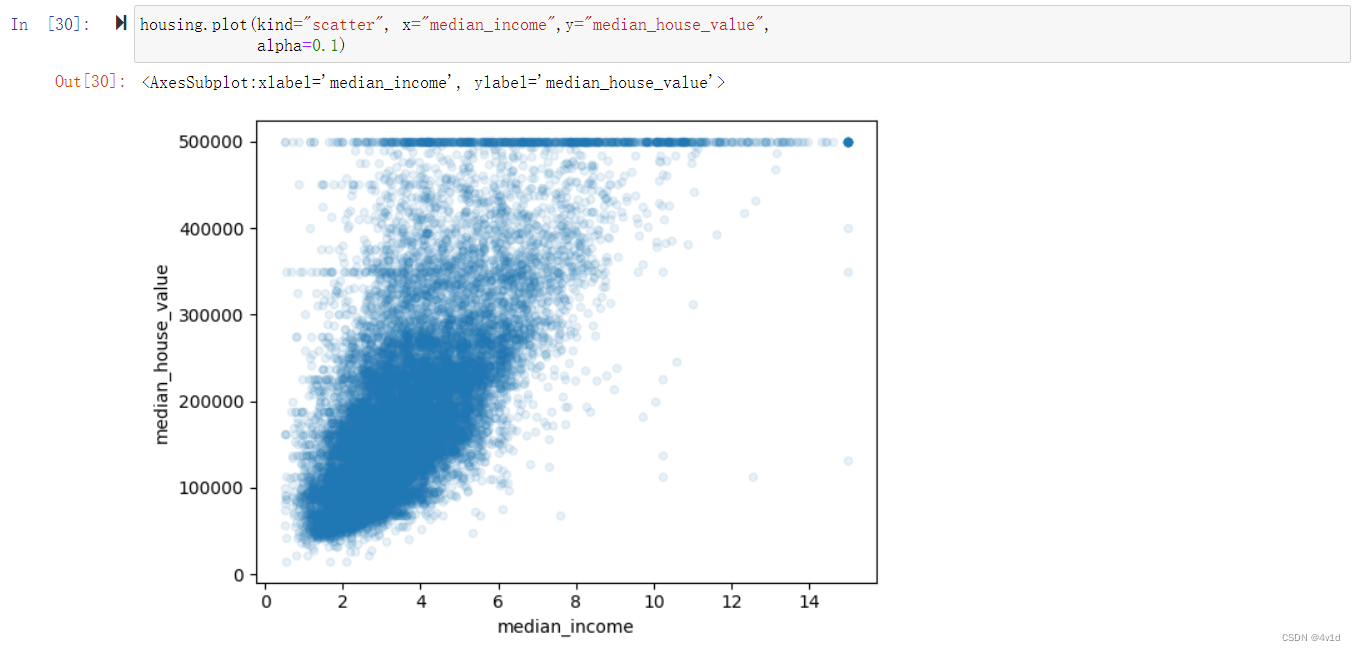
这张图说明了几点。首先,相关性非常高;可以清晰地看到向上的趋势,并且数据点不是非常分散。第二,我们之前看到的最高价,清晰地呈现为一条位于 500000 美元的水平线。这张图也呈现了一些不是那么明显的直线:一条位于 450000 美元的直线,一条位于 350000 美元的直线,一条在 280000 美元的线,和一些更靠下的线。你可能希望去除对应的街区,以防止算法重复这些巧合。