9.多数元素

news2024/11/27 2:21:57

文章目录

题目简介
题目解答
- 解法一：排序
- - 代码：
  - 复杂度分析：
- 解法二：摩尔投票法
- - 代码：
  - 复杂度分析：
- 解法三：哈希表
- - 代码
  - 复杂度分析：
题目链接

大家好，我是晓星航。今天为大家带来的是多数元素面试题相关的讲解！😀

题目简介

在这里插入图片描述

题目解答

解法一：排序

思路：如果蒋数组nums中的所有元素按照单调递增或单调递减的顺序排序，那么下标为[n/2] (下标从0开始) 的元素一定是众数。

代码：

class Solution {
    public int majorityElement(int[] nums) {
        Arrays.sort(nums);
        return nums[nums.length / 2];
    }
}

这里解法很简单，先用Arrays下的sort排序方法给数组排序，然后我们找到排序好之后的数组中间的元素即是出现最多的那个元素。

官方解答：
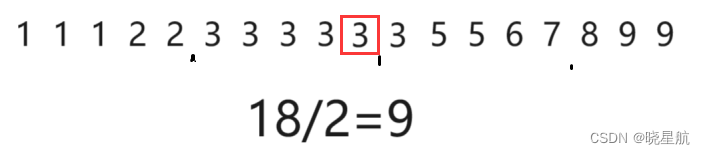
在这里插入图片描述

模拟演示：
在这里插入图片描述

复杂度分析：

时间复杂度：O(n log⁡ n)将数组排序的时间复杂度为 O(n log ⁡n)

空间复杂度：O(log⁡ n)。如果使用语言自带的排序算法，需要使用 O(log ⁡n)的栈空间。如果自己编写堆排序，则只需要使用 O(1) 的额外空间。

解法二：摩尔投票法

思路：
在这里插入图片描述

代码：

class Solution {
    public int majorityElement(int[] nums) {
        int cand_num = nums[0], count = 1;
        for (int i = 1; i < nums.length; ++i) {
            if (cand_num == nums[i])
                ++count;
            else if (--count == 0) {
                cand_num = nums[i];
                count = 1;
            }
        }
        return cand_num;
    }
}

在这里插入图片描述

复杂度分析：

时间复杂度：O(n)O(n)O(n)。Boyer-Moore 算法只对数组进行了一次遍历。
空间复杂度：O(1)O(1)O(1)。Boyer-Moore 算法只需要常数级别的额外空间。

解法二来源于力扣大佬 ̶.̶G̶F̶u̶＇̶ 、̶ ̶|的解法。

解法三：哈希表

我们使用哈希映射（HashMap）来存储每个元素以及出现的次数。对于哈希映射中的每个键值对，键表示一个元素，值表示该元素出现的次数。

我们用一个循环遍历数组 nums 并将数组中的每个元素加入哈希映射中。在这之后，我们遍历哈希映射中的所有键值对，返回值最大的键。我们同样也可以在遍历数组 nums 时候使用打擂台的方法，维护最大的值，这样省去了最后对哈希映射的遍历。

代码

class Solution {
    private Map<Integer, Integer> countNums(int[] nums) {
        Map<Integer, Integer> counts = new HashMap<Integer, Integer>();
        for (int num : nums) {
            if (!counts.containsKey(num)) {
                counts.put(num, 1);
            } else {
                counts.put(num, counts.get(num) + 1);
            }
        }
        return counts;
    }

    public int majorityElement(int[] nums) {
        Map<Integer, Integer> counts = countNums(nums);

        Map.Entry<Integer, Integer> majorityEntry = null;
        for (Map.Entry<Integer, Integer> entry : counts.entrySet()) {
            if (majorityEntry == null || entry.getValue() > majorityEntry.getValue()) {
                majorityEntry = entry;
            }
        }

        return majorityEntry.getKey();
    }
}

引用方法分析：

.get():根据map集合中元素的Key来获取相应元素的Value
.put():向map集合中添加Key为key，Value为value的元素，当集合中没有这个key时返回null，当集合中有这个key时返回前一个value。
.enterSet():返回 Map 中所有键值对的集合。每一个元素都是一个 Map.Entry 对象，其中包含一个 key 和一个 value。
.containsKey():判断 Map 中是否包含指定的 key
.getKey():获取Map中的key值
getValue():获取Map中的value值

复杂度分析：

时间复杂度：O(n)，其中 n 是数组 nums 的长度。我们遍历数组 nums 一次，对于 nums 中的每一个元素，将其插入哈希表都只需要常数时间。如果在遍历时没有维护最大值，在遍历结束后还需要对哈希表进行遍历，因为哈希表中占用的空间为 O(n)（可参考下文的空间复杂度分析），那么遍历的时间不会超过 O(n)。因此总时间复杂度为 O(n)。
空间复杂度：O(n)。哈希表最多包含 n−⌊n/2⌋个键值对，所以占用的空间为 O(n)。这是因为任意一个长度为 n 的数组最多只能包含 n 个不同的值，但题中保证 nums 一定有一个众数，会占用（最少） ⌊n/2⌋+1个数字。因此最多有 n−(⌊n/2⌋+1)个不同的其他数字，所以最多有 n−⌊n/2⌋个不同的元素。