感谢大佬的光临各位,希望和大家一起进步,望得到你的三连,互三支持,一起进步
个人主页:LaNzikinh-CSDN博客
c语言基础_LaNzikinh篮子的博客-CSDN博客
文章目录
- 一.爬楼梯问题
- 二.汉诺塔问题
- 总结
一.爬楼梯问题
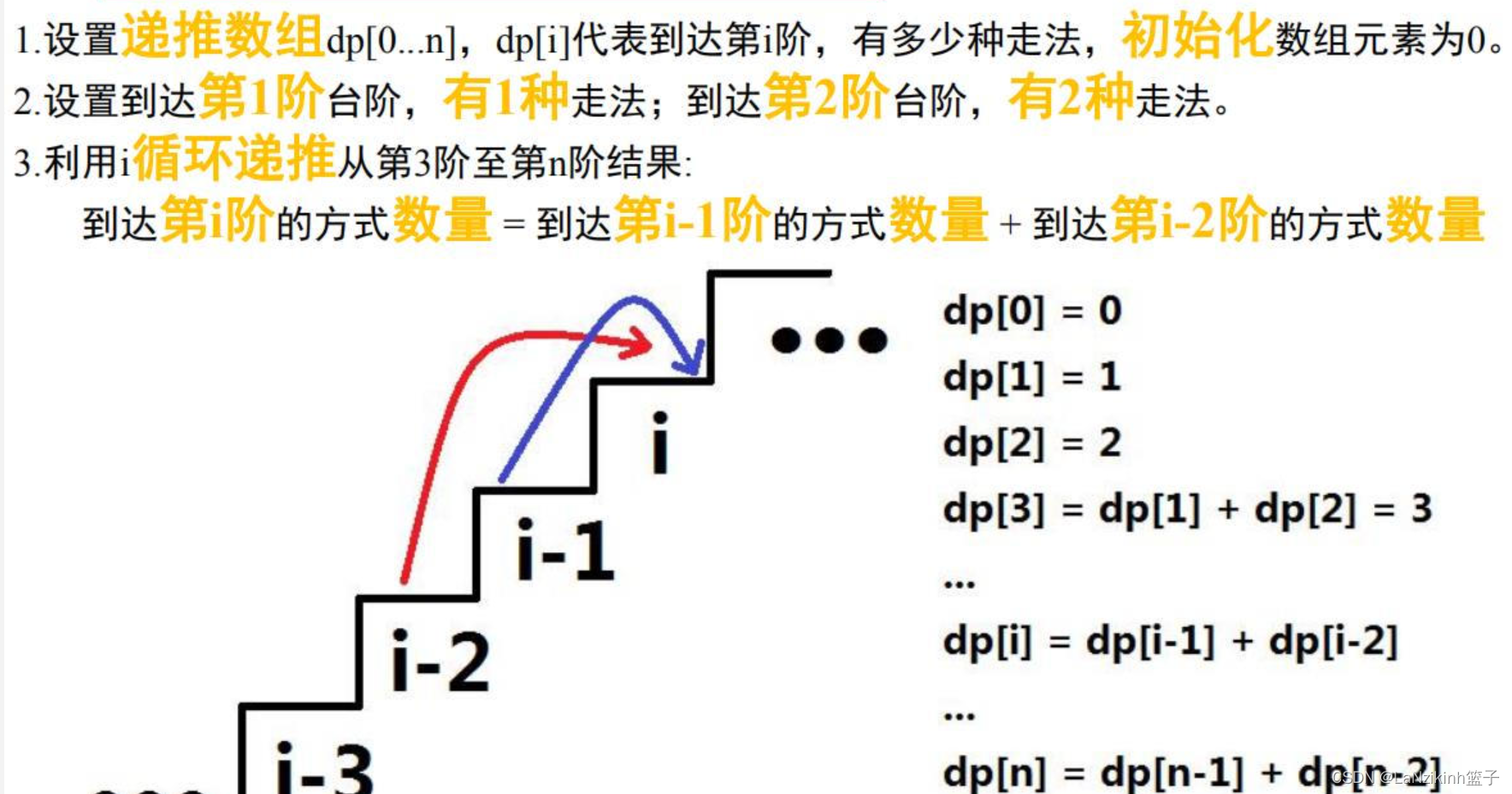
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?注意:给定 n 是一个正整数
这个问题就是一个非常典型的递归问题,但是拿到题目的时候真的没有什么思路,不知道怎么去思考
思路:
递归的核心思想就是把大问题变成小问题,我们先来找爬楼梯的小问题,最简单的就是爬一个或者爬两个,那我爬n个怎么说呢?我爬到第N个有两种上去的方法,一种是在N减一个的时候爬一个楼梯,另一种就是在N -2个的时候爬两个楼梯,所以是f(n)=f(n-1)+f(n-2)
int fun(int n)
{
if (n == 1)
return 1;
else if (n == 2)
return 2;
else
return f(n - 1) + f(n - 2);
}这里用的是深度优先遍历,这个还是比较简单的
二.汉诺塔问题
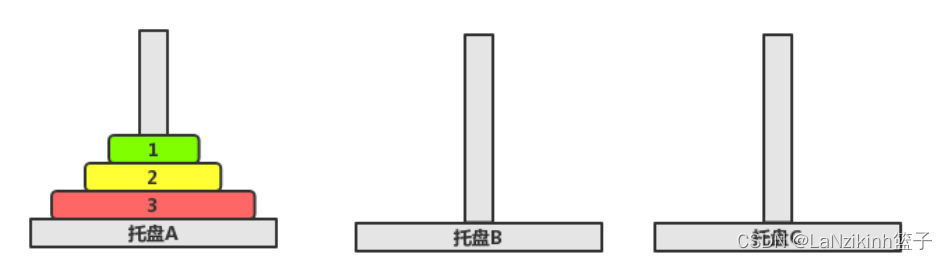
游戏的规则:汉诺塔游戏规则如下12:
- 有三根相邻的柱子,标号为A,B,C。
- A柱子上从下到上按金字塔状叠放着n个不同大小的圆盘。
- 现在把所有盘子一个一个移动到柱子B上,并且每次移动同一根柱子上都不能出现大盘子在小盘子上方。
- 每次只允许一个人移动碟子,且每次仅允许移动一个碟子的位置。
- 在团队所有成员必须依次移动盘子。
- 在任意一次移动中,较小的盘子不得被置于较大的盘子下方。
- 一次只能移动一个圆盘。
思路:A为起始柱子,B为中转柱子,C为目标柱子
注意:这些柱子在递归是会发生改变!!!
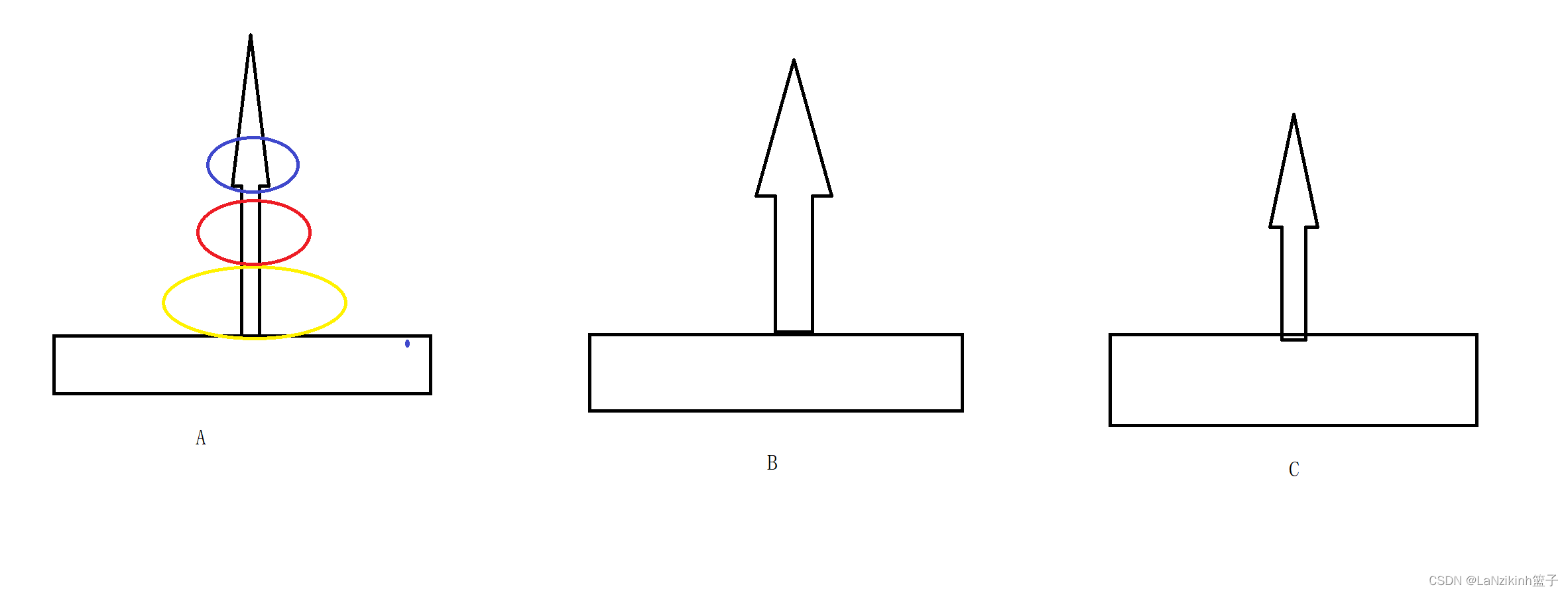
要想完成这个问题,首先得把上面两个放到中间去
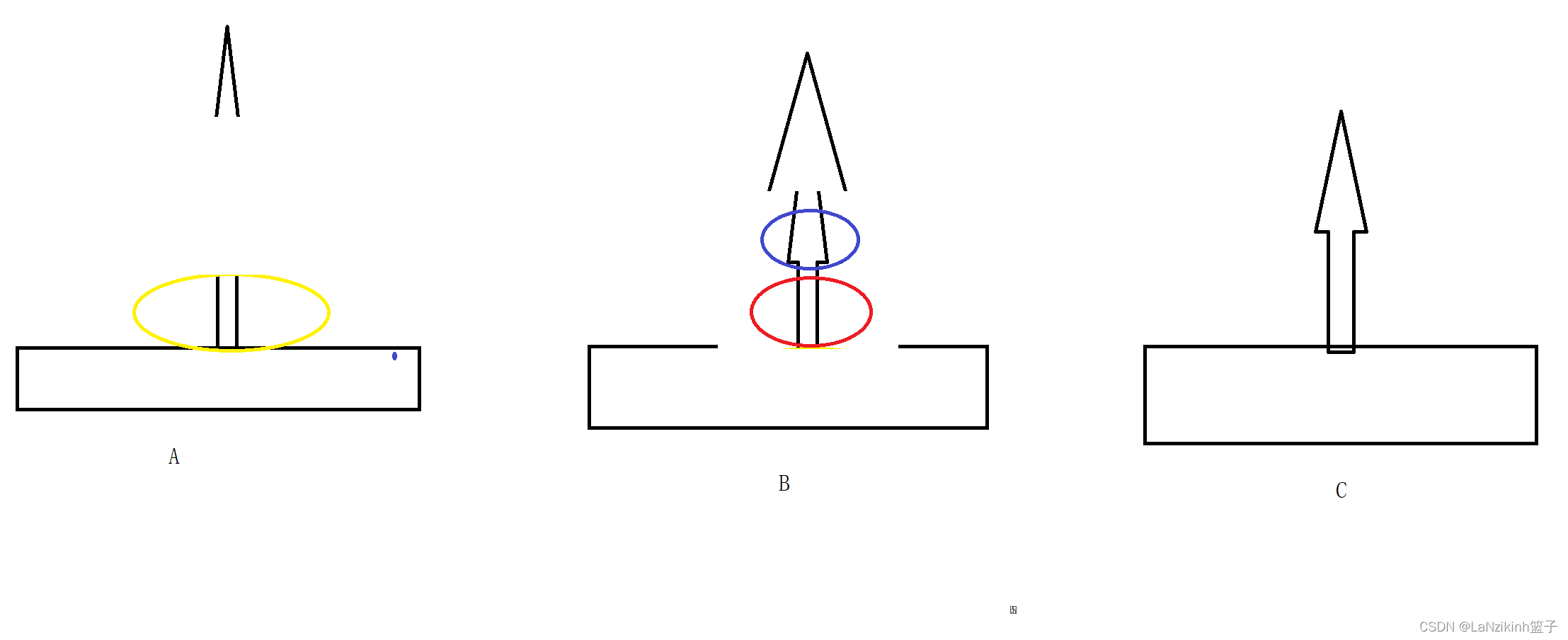
然后再把最底下的放到目标地方

再把中间的放到目标上就可以了
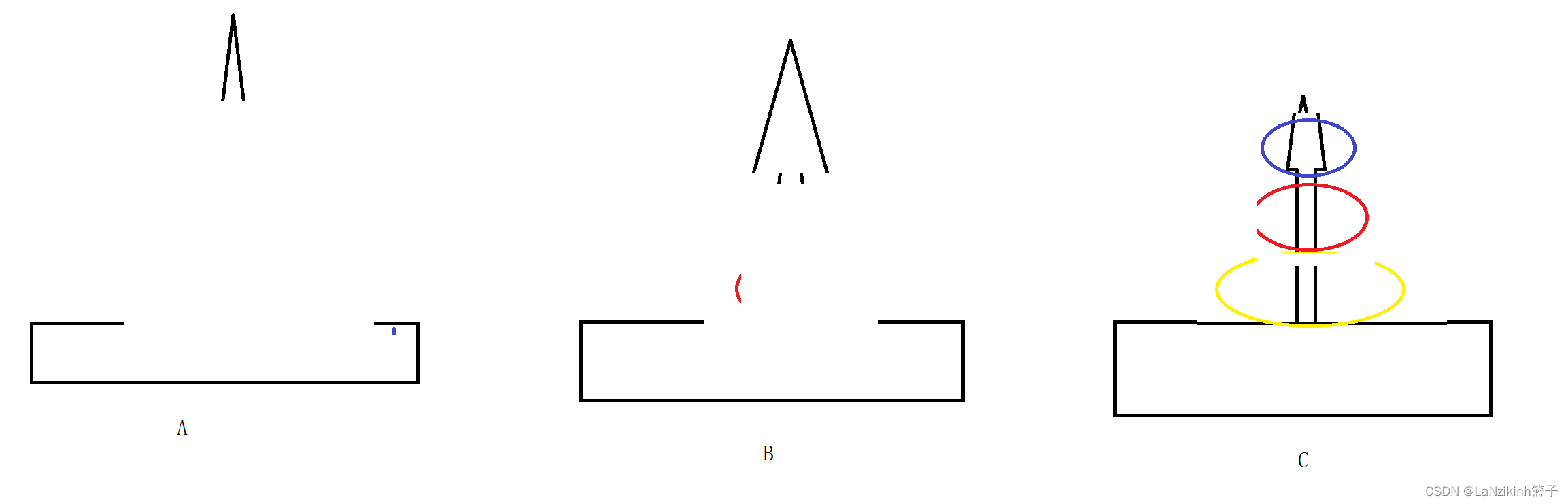
函数递归很好写,但是非常难理解
void hanoi(int n, char A, char B, char C) {
//n代表 A柱子上面的盘子数量
if (n == 1) {
move(n, A, C);//如果只有一个盘子,直接从A移动到C
}
else {
hanoi(n - 1, A, C, B);//将n-1个盘子从A移动到B
move(n, A, C);
hanoi(n - 1, B, A, C); //将n-1个盘子从B移动到C
}
}move为打印函数
void move(int n, char x, char y) {
printf("%c--->%c\n",x, y);
}
很多人理解了思想也写得出这个代码,但是就是想不通为什么完成了这个题目?
我觉得可能是因为没理解程序里面的参数是怎么回事,else里面的参数估计就有人看不明白了,在你第一次在主函数中把A,B,C 这三个字符输进去的时候,调用函数是没问题的,形参和实参一一对应,hanoi函数里面的A,B,C就对应着'A', 'B','C'三个柱子,但是你一旦开始递归,第一次递归函数里面的三个参数A,B,C代表的就是柱子'A',柱子'C',柱子'B' 了,每一次递归A,B,C三个参数代表的柱子都在不断的跳动,所以函数printf里面的从A到C进行输出,其实真正打印出来的各种移动情况都有,而else里面的第一句话执行完毕后,就是实现了把第一个柱上除了最后一个盘子上面的所有盘子移到了B,第二句其实是最初的参数和柱子对应的A和C,即把最后一个从A移到C,第三句又是把所有的从B移到C。函数本身参数是定死的,但是那三个参数却可以代表不同的真实的具体哪个柱子上的盘子进行移动,而参数的位置代表的是移动的思想。
总结
这两个问题是很好的递归问题,递归难就难在写出来简单,但是真正理解起来还是有一定的思考量的