2023年数维杯国际大学生数学建模挑战赛B题棉花秸秆热解的催化反应解题全过程论文及程序

2023年数维杯国际大学生数学建模挑战赛

B题棉花秸秆热解的催化反应

原题再现：

随着全球对可再生能源需求的不断增加，生物质能作为一种成熟的可再生能源得到了广泛的关注。棉秆作为一种农业废弃物，由于其富含纤维素、木质素等生物质成分，被认为是重要的生物质资源。棉秆热解可以产生多种形式的可再生能源，但其热解产物的质量和收率受热解温度、催化剂等因素的影响。因此，研究棉秆热解产物的机理和性质（名词定义见附录），研究热解过程中催化剂的作用机理和效果，对棉秆的高效利用和可持续发展具有重要意义。
某化工实验室采用模型化合物法建立了脱硫灰与棉秆、脱硫灰与模型化合物的热解组合。采用不同配比的热解组合，研究了脱硫灰对棉秆热解产物生成的催化机理和影响。同时，在选择模型化合物时，需要考虑其在实验过程中反应性能的可控性和稳定性，以及对棉秆热解的贡献。纤维素低聚糖（CE）和木质素（LG）是棉秆中纤维素和木质素的代表性组分，可以表征棉秆本身的生物量特性。选择这两种组分作为模型化合物，可以更精细地控制实验条件，研究脱硫灰对不同生物质组分的靶向催化作用。因此，选择CE和LG作为模型化合物是基于对棉秆本身生物量组成和化学结构特征的合理判断。实验结果见附录1和附录2。
采用固定床热解方法，在10/100、20/100、30/100、40/100、50/100、60/100、80/100、100/100的混合比例下进行脱硫灰/生物质热解实验。混合比的选择是基于这样一个事实：在这些实验条件下，平行实验的相对误差约为5%。如果混合比太小，如5/100或7/100，相对误差会对实验结果产生显著影响，严重影响实验的探索和优化过程。如果能够利用数学模型和人工智能学习在有限的数据条件下预测热解产物的产率或产量，不仅可以大大减少实验优化所需的时间，而且可以对热解产物分布的变化趋势提供准确的指导。

请通过数学建模完成以下问题：
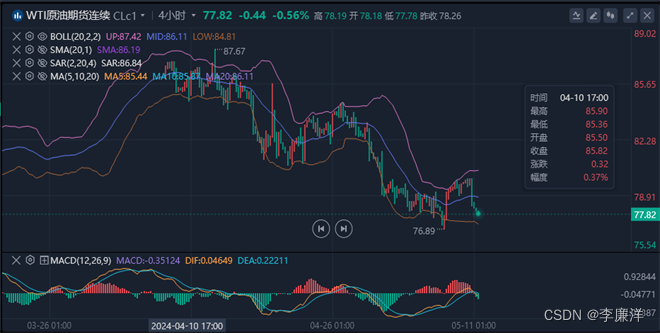
（1）对于附录I中的每个热解组合，分析热解产物（焦油、水、焦渣、合成气）的产率与相应热解组合的混合比的关系，并说明脱硫灰作为催化剂是否在促进棉秆、纤维素和木质素的热解中起到重要作用？
（2）根据附录II，针对三种热解组合中的每一种，讨论了热解组合的混合比对每组热解气体产率的影响，并通过制作相应图像进行了解释。
（3）在相同比例脱硫灰的催化作用下，CE和LG热解产物的产率以及热解气体组分的产率是否存在显著差异？请提供理由。
（4）如何建立脱硫灰对CE、LG等模型化合物的催化反应机理模型和反应动力学模型进行分析？
（5）请使用数学模型或AI学习方法在有限的数据条件下对热解产物的产量或数量进行预测。

整体求解过程概述(摘要)

随着全球对可再生能源需求的增加，棉秆作为一种重要的生物质资源，近年来备受关注。根据不同催化热解反应条件下棉秆热解产物和热解气体产物的数据，对棉秆的有效利用和可持续发展进行了研究。
数据预处理。对于问题给出的数据，首先绘制散点图对给定的数据集进行粗略分析。然后利用数据集绘制q-q图并进行Shapiro-Wilk检验，判断问题给出的数据集服从正态分布。
对于第一个问题，为了分析各热解组合的热解产物收率与相应热解组合的混合比之间的关系。首先，绘制并讨论了不同配比下热价产物的折线图。然后引入人相关分析，对不同配比下不同产品的收率进行相关分析。如焦油收率与DFA/CS比的相关系数为-0.8827，表现出较强的负相关。然后进行多项式回归拟合，利用二阶多项式曲线拟合散点图趋势。最后通过函数关系判断热解产物与混合比的关系。为了验证脱硫灰作为催化剂的重要性，分别比较了脱硫灰作为催化剂条件下的反应结果。
对于第二个问题，利用matlab绘制了三种热解组合的折线图，并利用第一个问题的二阶多项式曲线拟合方法得到了函数关系。利用图像和函数关系进行讨论和分析，解释了不同混合比下的变化过程，解释了各组热解气体的不同结果。例如，随着DFA/CS比的增加，H2的产率显著增加。这可能说明脱硫灰促进了催化反应中H2的释放，可能是因为脱硫灰影响了热解过程中的热解反应，促进了H2的生成。
对于第三个问题，对于混合比相同的情况，采用秩和检验法进行显著性分析。例如，观察CE和LG热解产物产率差异的分析结果，比较P值与0.05之间的关系，确定是否存在显著差异。焦油、焦炭和合成气产率的P值在0.0002左右时非常小（接近于零），远低于标准显著性水平0.05，表明DFA/CE和DFA/LG比率下焦油产率之间存在统计学显著差异。
对于第四个问题，通过热解反应过程论证了反应机理，并根据反应路径的特点和Arrhenius方程查询相关参数，建立了反应动力学模型。
对于第五个问题，利用BP神经网络进行预测，指定输入指标和输出指标，划分训练集和测试集，调整和训练模型参数，然后对测试集的数据进行预测，最后进行误差分析。本文根据BP神经网络预测模型，选取附录1中DAF/CS组的数据作为训练集，对预测模型进行训练，并对测试集的测试结果进行预测。拟合系数R为0.9993，相对误差很小，说明拟合效果很好。

问题分析：

问题一分析
为解决问题1，为了分析各热解组合的热解产物收率与对应热解组合的混合比之间的关系，首先绘制了不同混合比下热解产物收率的折线图，通过对折线图的分析得到了一般关系。然后采用Pearson相关分析法对不同配比下不同产品的收率进行分析。通过相关分析，建立了以混合比为自变量，以产品产量为因变量的回归分析模型。为了验证脱硫灰作为催化剂是否能促进棉秆、纤维素和木质素的热解，得到了各函数的一阶导数，并分析和解释了催化剂对热解的影响。
问题二分析
为了解决问题2，利用matlab绘制了三种热解组合的图像。利用问题1的二阶多项式曲线拟合方法得到了函数关系，并对图像和函数关系进行了讨论和分析，解释了不同混合比下的变化过程，解释了各组热解气体的不同结果。
问题三分析
针对问题3，对于相同的混合比，采用秩和检验法进行显著性分析，并观察显著性差异分析的结果。
问题4的分析
为解决问题4，通过热解反应过程论证了反应机理，并根据反应路径的特点和Arrhenius方程查询相关参数，建立了反应动力学模型。
问题五分析
针对问题5，采用BP神经网络进行预测，指定输入指标和输出指标，划分训练集和测试集，调整和训练模型参数，对测试集数据进行预测并进行误差分析。

模型的建立与求解整体论文缩略图

在这里插入图片描述

全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可

程序代码：

function [RMSE, MAPE, R2] = calculate_metrics(actual, predicted)
 % Calculate root mean square error (RMSE)
 RMSE = sqrt(mean((actual - predicted).^2));
 % Calculate Average Absolute Percentage Error (MAPE)
 MAPE = mean(abs((actual - predicted) ./ actual)) * 100;
 % Calculate the coefficient of determination (R2)
 ssRes = sum((actual - predicted).^2);
 ssTot = sum((actual - mean(actual)).^2);
 R2 = 1 - (ssRes / ssTot);
End
function eq = generateFitEquation(coeffs, modelType)
 if startsWith(modelType, 'poly')
 % for polynomial models
 degree = str2double(extractAfter(modelType, 'poly')) - 1;
 terms = cell(1, length(coeffs));
 % Constructing polynomial equations item by item
 for idx = 1:length(coeffs)
 coeff = coeffs(idx);
 power = degree - idx + 1; 
 if power == 0
 terms{idx} = sprintf('%f', coeff);
 elseif power == 1
 terms{idx} = sprintf('%f*x', coeff);
 else
 terms{idx} = sprintf('%f*x^%d', coeff, power);
 end
 end
 eq = strjoin(terms, ' + ');
 elseif any(strcmp(modelType, {'exp1', 'exp2'}))
 % For exponential models, add equation generation logic for exponential models
 eq = 'exp model equation here...';
 else
 eq = 'Other model equation here...';
 end
end
data=[19.46 26.84 29.21 24.49
17.25 27.64 29.11 26
15.43 28.11 29.3 27.16
14.14 28.23 29.34 28.29
13.89 28.62 29.14 28.35
13.21 29.01 29.33 28.45
12.84 30.07 29.47 27.62
12.57 30.68 29.64 27.11
12.13 31.02 29.87 26.98
];
numCols = size(data, 2);
% Go through each column and perform the Jarque-Bera test
for i = 1:numCols
 [h, p] = jbtest(data(:, i));
 if h == 0
 fprintf('Column %d data follows a normal distribution (p-value = %.5f)\n', i, p);
 else
 fprintf('Column %d data does not follow a normal distribution (p-value = %.5f)\n', i, p);
 end
end
% Select the column for which you want to plot a normal probability graph
selectedColumns = [1, 2, 3,4];
% Plot a normal probability plot for each column
for i = selectedColumns
 figure;
 normplot(data(:, i));
 hold on;
 h = probplot(gca,'normal');
 set(h,'marker','*');
 title(sprintf('Normal probability graph - Column %d', i));
 hold off;
end

DFA_CS = [0, 10, 20, 30, 40, 50, 60, 80, 100]; % Due to the naming requirements of the matlab 
language, DFA CS is used instead of DFA/CS
TarYield = [19.46, 17.25, 15.43, 14.14, 13.89, 13.21, 12.84, 12.57, 12.13];
WaterYield = [26.84, 27.64, 28.11, 28.23, 28.62, 29.01, 30.07, 30.68, 31.02];
CharYield = [29.21, 29.11, 29.3, 29.34, 29.14, 29.33, 29.47, 29.64, 29.87];
SyngasYield = [24.49, 26, 27.16, 28.29, 28.35, 28.45, 27.62, 27.11, 26.98];
% Create a graphics window，Draw scatter line plots
figure;
hold on; %Make the graphics appear on a picture
% Scatter plot and line plot of yield of four kinds of products were drawn
scatter(DFA_CS, TarYield, 'filled');
plot(DFA_CS, TarYield, 'DisplayName', 'Tar Yield');
scatter(DFA_CS, WaterYield, 'filled');
plot(DFA_CS, WaterYield, 'DisplayName', 'Water Yield');
scatter(DFA_CS, CharYield, 'filled');
plot(DFA_CS, CharYield, 'DisplayName', 'Char Yield');
scatter(DFA_CS, SyngasYield, 'filled');
plot(DFA_CS, SyngasYield, 'DisplayName', 'Syngas Yield');
% add legend
legend show;
%Add title and axis labels
title('Yield of Decomposition Products vs DFA/CS Ratio');
xlabel('DFA/CS Ratio');
ylabel('Yield (wt.%)');
% Display grid
grid on;
% end
hold off;