今日备忘录: "不破不立. "
本文索引
- 1. 前言
- 2. 顺序表与链表的区别
- 3. 什么是栈
- 4. 栈的实现
- 5. OJ括号匹配
- 6. 总结
1. 前言
人总是在坍塌中重建, 有些东西必须摧毁, 才能迎来新生, 不管是那些消耗你的人, 还是令你感到焦虑的事情, 还是一份你觉得毫无意义并且又不喜欢的工作, 又或者是那个内心敏感的自己, 总之你害怕什么, 就要去面对什么, 你想要什么, 就要去靠近什么, 在声色名利中守住本性, 在世俗目光中信步前行, 大浪淘沙, 去伪存真, 破而后立, 否极泰来.
本文旨在探讨数据结构中栈的实现以及顺序表与链表区别总结.
更多精彩, 期待关注 主页: 酷酷学!!!
2. 顺序表与链表的区别
在实现栈之前, 我们先总结一下顺序表和链表
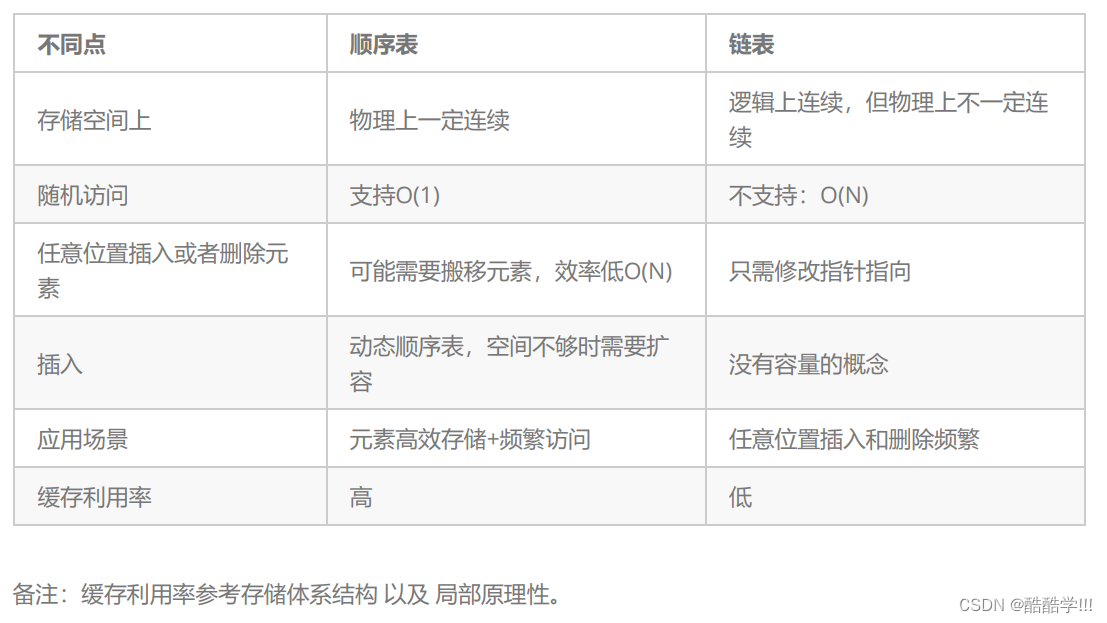
以上是顺序表与链表比较全面的区别总结, 在插入数据时链表没有容量的概念指的是链表的空间是使用多少开辟多少, 不会进行扩容操作, 也不会造成容量的浪费.
那么什么是缓存利用率,简单讲解一下
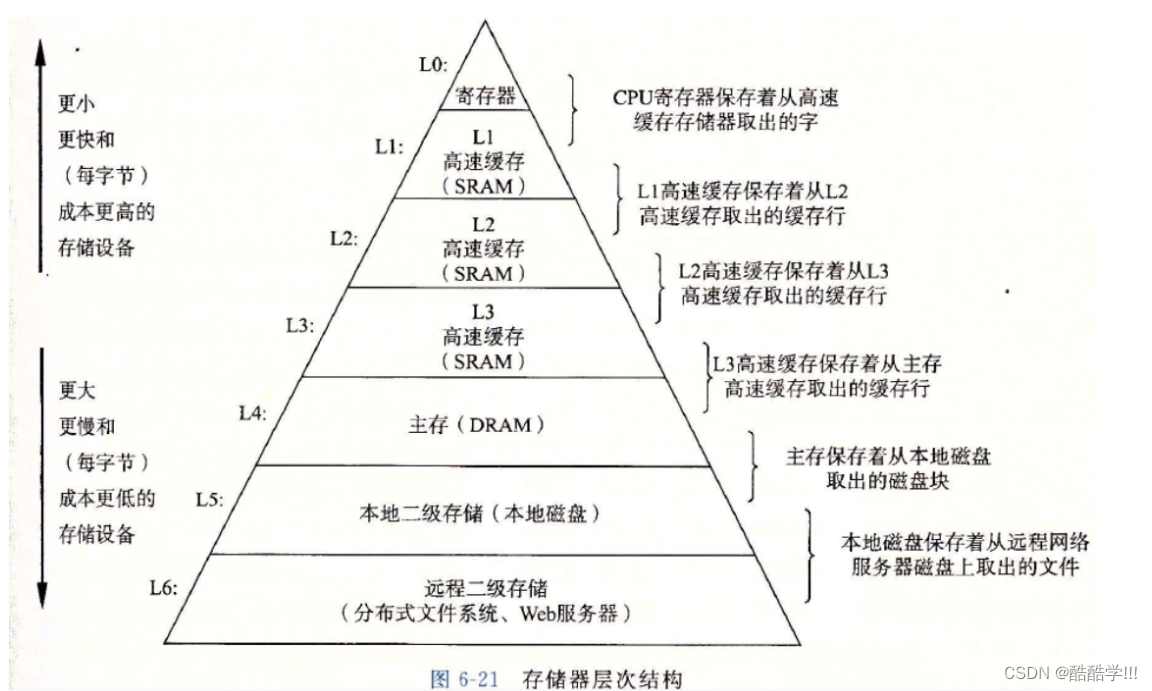
以上是存储器的结构层次,由于CPU的访问速度非常的快, 它不会直接访问内存, 因为内存的读写速度太慢了, 而是将数据先逐层转移到寄存器或者高速缓存中,在进行读写, 一般寄存器存放字节大小为8的数据, 然后CPU再进行访问, 但是如何将数据转移到缓存当中的呢, 为什么说顺序表缓存利用率高而链表低呢?
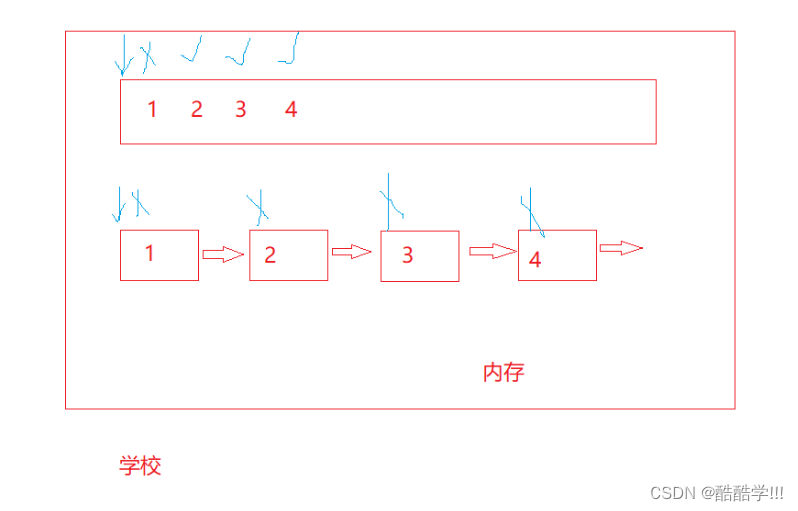
在将内存中的数据运送到缓存中的时候, 不是一个一个传输的,而是将连带后面的一块空间直接一起运送到缓存中, 如同一辆大巴车一样, 不是一个一个运送, 而是包括后面的一块空间一起运输, 然后CPU在从缓存中进行读写, 那么, 如果继续往后读写, 在缓存中, 我们称之为缓存命中, 直接访问, 如果不在缓存中, 我们称之为不命中, 要把数据从内存加载到缓存中, 在进行访问, 如此看来所以 顺序表的缓存利用率肯定高于链表
更多资讯, 可以点击参考 与程序员相关的CPU缓存知识
3. 什么是栈
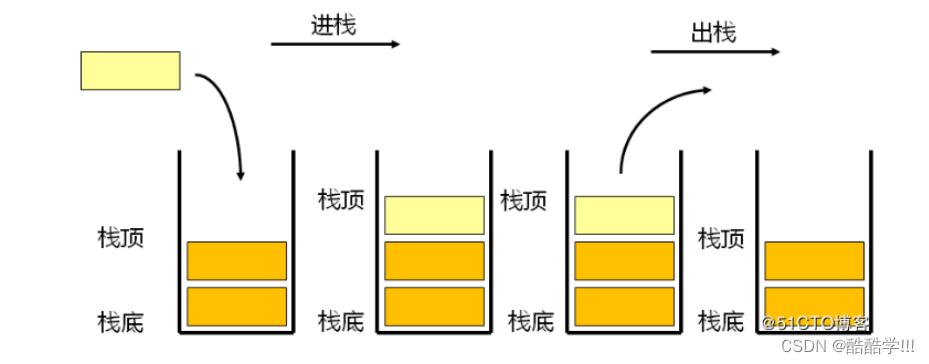
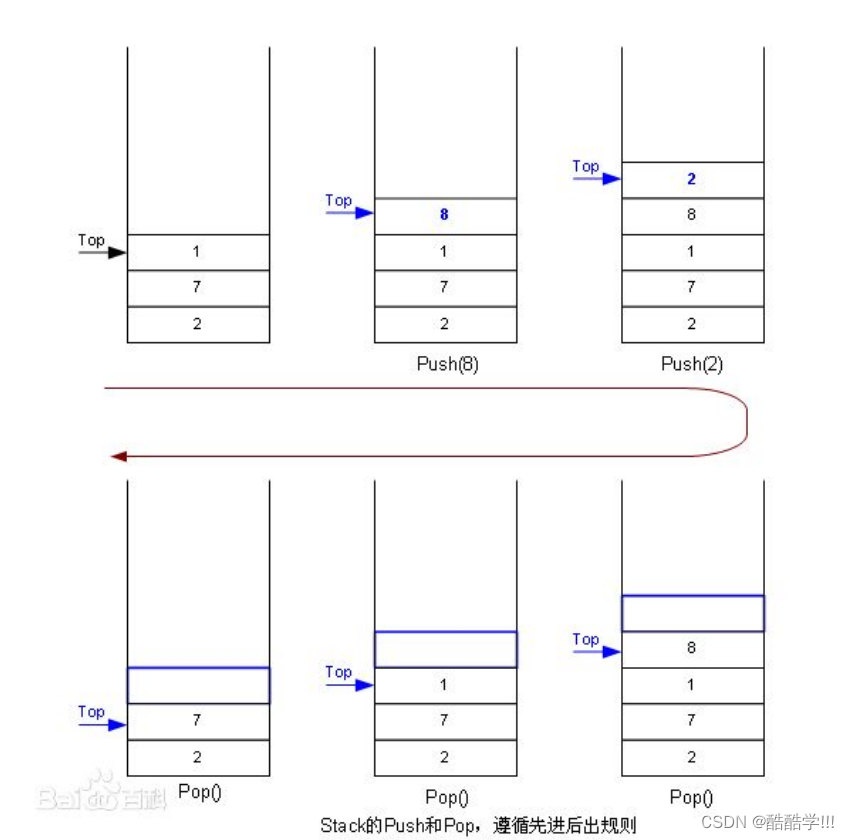
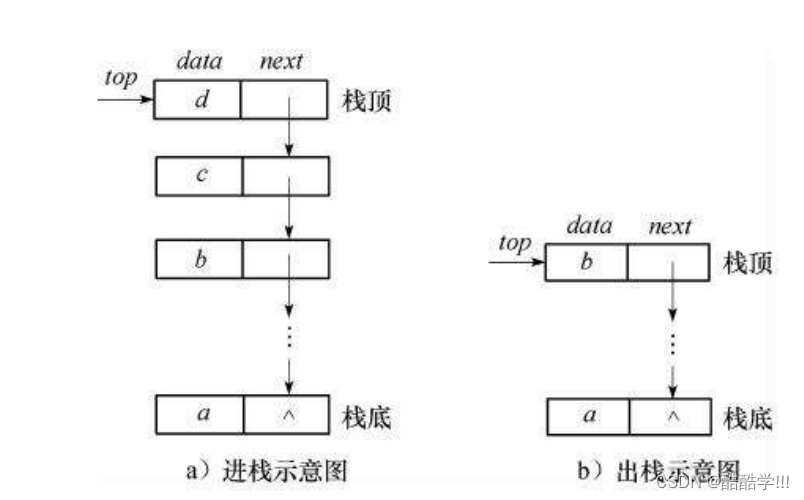
栈: 一种特殊的线性表, 其只允许在固定的一端进行插入和删除元素操作. 在进行数据插入和删除操作的一端称之为栈顶, 另一端称之为栈底. 栈中的元素遵守后进先出LIFO(Last In First Out)原则.
压栈 : 栈的插入操作叫做压栈或入栈, 入数据在栈顶
出栈 : 栈的删除操作叫做出栈. 出数据也在栈顶.
4. 栈的实现
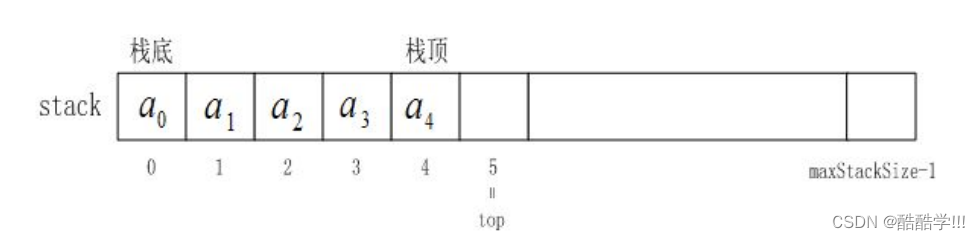
栈的实现一般可以使用数组或者链表进行实现, 相对而言数组的结构实现更优一些, 因为在数组上尾插数据的代价比较小, 而且数组的缓存利用率比较高.
第一步:
创建三个文件
在头文件中进行结构定义和函数声明
#pragma once
#include<stdio.h>
#include<stdlib.h>
#include<assert.h>
#include<stdbool.h>
typedef int STDatatype;
typedef struct Stack
{
STDatatype* a;
int top;
int capacity;
}ST;
//初始化
void InitStack(ST* pst);
//销毁
void Destory(ST* pst);
//压栈
void Push(ST* pst,STDatatype x);
//出栈
void Pop(ST* pst);
//取栈顶元素
STDatatype STTop(ST* pst);
//判空
bool Empty(ST* pst);
//获取元素个数
int Size(ST* pst);
第二步:
实现栈的方法
- 初始化
void InitStack(ST* pst)
{
assert(pst);
pst->a = NULL;
pst->capacity = pst->top = 0;
}
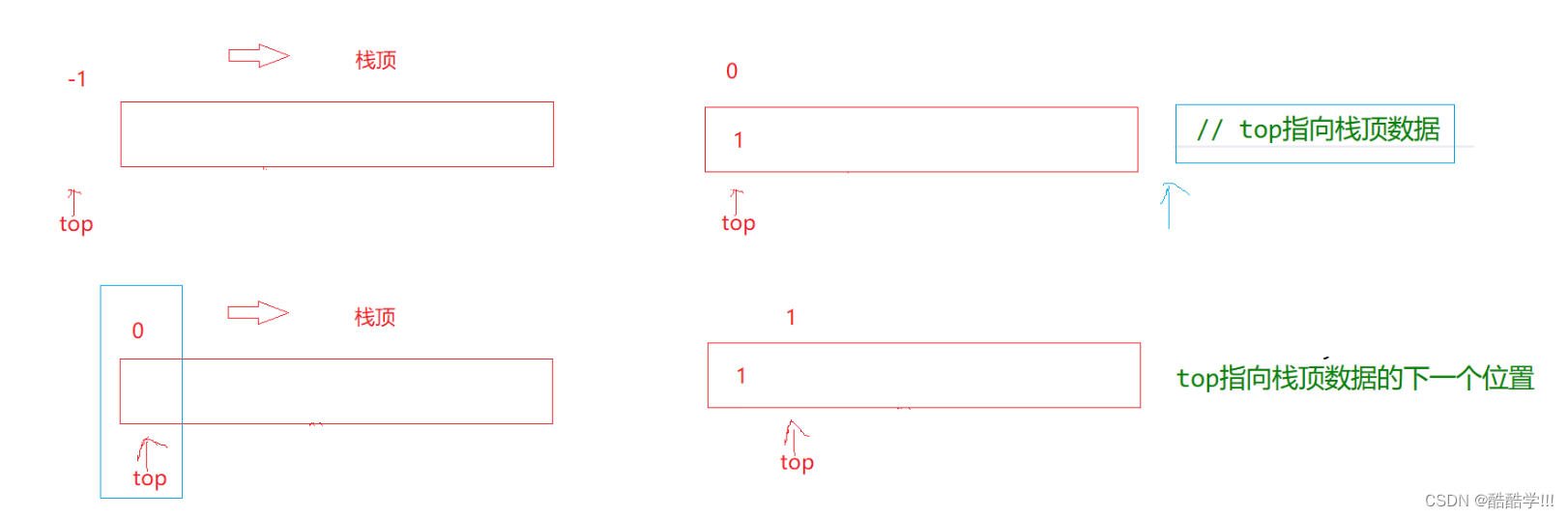
注意
top的值根据自己的情况定义, 若top=0,表示指向栈顶数据下一个位置, top=-1,表示指向栈顶数据.
首先断言,这里肯定不能给我传一个NULL, 然后进行常规操作
- 销毁
void Destory(ST* pst)
{
assert(pst);
free(pst->a);
pst->a = NULL;
pst->top = pst->capacity = 0;
}
动态顺序表, 空间需要手动释放
- 压栈
void Push(ST* pst, STDatatype x)
{
assert(pst);
if (pst->capacity == pst->top)
{
int Newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
STDatatype* tmp = (STDatatype*)realloc(pst->a,sizeof(STDatatype) * Newcapacity);
if (tmp == NULL)
{
perror("malloc fail");
return;
}
pst->a = tmp;
pst->capacity = Newcapacity;
}
pst->a[pst->top] = x;
pst->top++;
}
因为我们初始化的时候没有开辟空间, 所以如果栈为空的时候, 我们先开辟四个空间, 当栈满时, 我们在成倍扩容, 然后先用临时变量存储首地址, 防止申请失败原地址丢失, 然后更改空间容量大小, 最后在进行写入数据.
- 销毁
void Pop(ST* pst)
{
assert(pst);
assert(pst->top > 0);
pst->top--;
}
首先栈不能为NULL, 并且需要有数据, 然后直接top-- 就行.
- 获取栈顶元素
STDatatype STTop(ST* pst)
{
assert(pst);
assert(pst->top > 0);
return pst->a[pst->top-1];
}
直接返回top的前一个位置
- 判断栈是否为空
bool Empty(ST* pst)
{
assert(pst);
return pst->top == 0;
}
如果top为0则栈为空
- 获取数据个数
int Size(ST* pst)
{
assert(pst);
return pst->top;
}
top表示下标, 也就是元素个数
5. OJ括号匹配
题目链接: 有效的括号
题目描述:

题目分析:
首先题目有三个要求
- 左括号必须用相同类型的右括号进行闭合.
- 左括号必须以正确的顺序闭合
- 每个左括号都有一个对应相同类型的左括号
如果我们直接用左括号个数与右括号进行比较的话, 那么顺序问题我们无法解决, 而栈这种后进先出的结构恰好可以解决这种问题, 当遇到左括号时进行压栈, 遇到右括号时将左括号出栈, 进行比较, 正好解决了顺序问题, 但是C语言没有栈这种结构, 所以我们需要自己写栈这种结构.
于是我们很容易写出下面的代码.
bool isValid(char* s) {
ST stack;
InitStack(&stack);
while (*s)
{
//左括号压栈
if (*s == '(' || *s == '{' || *s == '[')
{
Push(&stack, *s);
s++;
}
//右括号与栈顶左括号进行匹配
else
{
char tmp = STTop(&stack);
Pop(&stack);
//如果不匹配
if ((tmp == '(' && *s != ')')
|| (tmp == '[' && *s != ']')
|| (tmp == "{" && *s != '}'))
{
return false;
Destory(&stack);
}
}
}
return true;
Destory(&stack);
}
但是这样写真的对吗, 答案是错的, 因为如果只有左括号的情况, 和只有右括号的情况, 我们还需要加以判断. 修正代码
字符串只有右括号, 先判断栈是否为空, 若为空返回false,并且释放栈
字符串只有左括号, 循环结束, 看看栈中元素还有没有, 如果还有则返回false,并且销毁栈
bool isValid(char* s) {
ST stack;
InitStack(&stack);
while (*s) {
// 左括号压栈
if (*s == '(' || *s == '{' || *s == '[') {
Push(&stack, *s);
}
// 右括号与栈顶左括号进行匹配
else {
if (Empty(&stack)) {
Destory(&stack);
return false;
}
char tmp = STTop(&stack);
Pop(&stack);
// 如果不匹配
if ((tmp == '(' && *s != ')') || (tmp == '[' && *s != ']') ||
(tmp == '{' && *s != '}')) {
Destory(&stack);
return false;
}
}
++s;
}
bool ret = Empty(&stack);
Destory(&stack);
return ret;
}
全部代码如下:
typedef char STDatatype;
typedef struct Stack {
STDatatype* a;
int top;
int capacity;
} ST;
// 初始化
void InitStack(ST* pst);
// 销毁
void Destory(ST* pst);
// 压栈
void Push(ST* pst, STDatatype x);
// 出栈
void Pop(ST* pst);
// 取栈顶元素
STDatatype STTop(ST* pst);
// 判空
bool Empty(ST* pst);
// 获取元素个数
int Size(ST* pst);
void InitStack(ST* pst) {
assert(pst);
pst->a = NULL;
pst->capacity = pst->top = 0;
}
void Destory(ST* pst) {
assert(pst);
free(pst->a);
pst->a = NULL;
pst->top = pst->capacity = 0;
}
void Push(ST* pst, STDatatype x) {
assert(pst);
if (pst->capacity == pst->top) {
int Newcapacity = pst->capacity == 0 ? 4 : pst->capacity * 2;
STDatatype* tmp =
(STDatatype*)realloc(pst->a, sizeof(STDatatype) * Newcapacity);
if (tmp == NULL) {
perror("malloc fail");
return;
}
pst->a = tmp;
pst->capacity = Newcapacity;
}
pst->a[pst->top] = x;
pst->top++;
}
void Pop(ST* pst) {
assert(pst);
assert(pst->top > 0);
pst->top--;
}
STDatatype STTop(ST* pst) {
assert(pst);
assert(pst->top > 0);
return pst->a[pst->top - 1];
}
bool Empty(ST* pst) {
assert(pst);
return pst->top == 0;
}
int Size(ST* pst) {
assert(pst);
return pst->top;
}
bool isValid(char* s) {
ST stack;
InitStack(&stack);
while (*s) {
// 左括号压栈
if (*s == '(' || *s == '{' || *s == '[') {
Push(&stack, *s);
}
// 右括号与栈顶左括号进行匹配
else {
if (Empty(&stack)) {
Destory(&stack);
return false;
}
char tmp = STTop(&stack);
Pop(&stack);
// 如果不匹配
if ((tmp == '(' && *s != ')') || (tmp == '[' && *s != ']') ||
(tmp == '{' && *s != '}')) {
Destory(&stack);
return false;
}
}
++s;
}
bool ret = Empty(&stack);
Destory(&stack);
return ret;
}
6. 总结
栈是一种线性数据结构,具有后进先出(LIFO)的特点,即最后进入栈的元素最先被访问或删除。栈通常有两种基本操作:压栈(push)和弹栈(pop),分别用于将元素压入栈顶和从栈顶弹出元素。
栈的应用非常广泛,常见的应用包括表达式求值、函数调用、浏览器的前进后退功能等。在计算机科学中,栈也被用于实现递归算法、解决括号匹配等问题。
栈的实现方式有多种,包括基于数组和基于链表的实现。基于数组的实现通常需要指定栈的最大容量,而基于链表的实现则可以动态调整大小。
总的来说,栈是一种非常重要且常用的数据结构,掌握栈的基本操作和应用场景对于理解算法和数据结构有着重要的意义。
如果此文有帮助 感谢点赞关注!!!