序言
在学习数据库之前,博主觉得有必要学习B树系列,以便之后更好地了解其原理,既然说到这里了,那就再说几句,数据库是帮助我们管理存在硬件当中的数据,如果要从中读取数据,就要考虑到硬件的读取速度目前大概在ms级别,即10的负3次方秒,说到这你可能会觉得硬件读取也不慢,但是没有对比就没有伤害,内存的读取速度目前在ns级别,即10的负9次方秒,两者之间相差100万倍,这个可是很恐怖的,也就是说内存IO1秒做的功,磁盘要花费12天才能做完,这可谓之一个天上一个地下。那么为了提高在磁盘中查找数据的效率,就要尽可能降低磁盘IO次数。如何降低呢?嘿嘿,那我就要问你心里有 " B树 " 么?
一、概要
1.概念
- B树,简而言之是一棵多叉树,具体是一棵M路的平衡搜索树,也可以是空树。M要大于2。
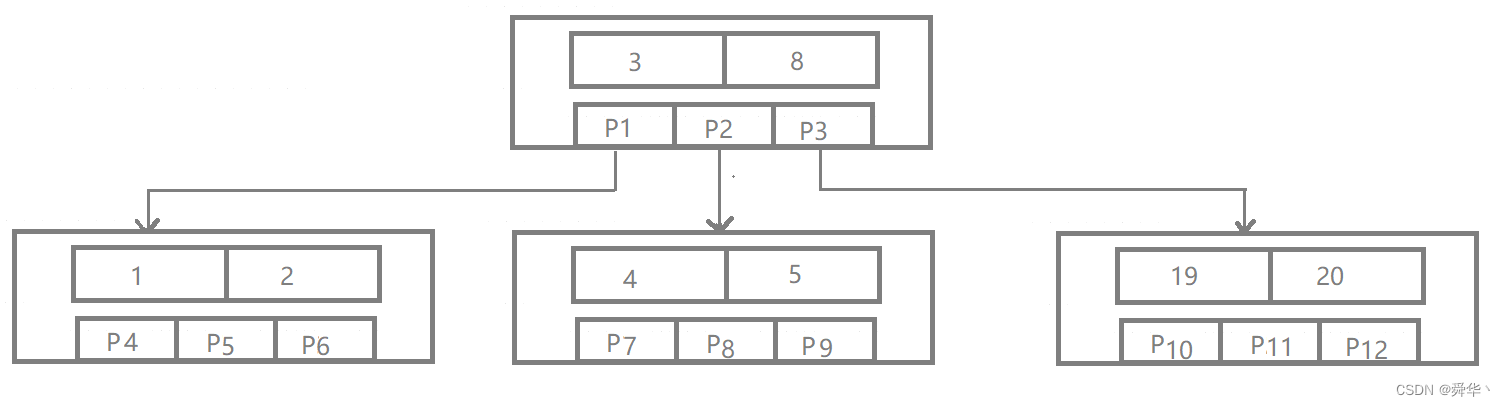
光看文字可能没有什么感觉,下面给出一张图,大致理解一下B树的结构:
图1:
首先,平衡指的是最高和最低子树的高度差在某一特定的区间,对于B树来说,可以达到「绝对平衡」,即最长路径和最短路径的高度相等。拓展一下,对于AVL树来说,可以达到「严格平衡」,即任意两子树的高度差不能大于1;对于红黑树来说,可以达到「相对平衡」,即最长路径小于等于最短路径的两倍。
补充:
- 红黑树,一种近似平衡的二叉搜索树,搜索的时间复杂度为O(log N)。
- AVL树,一种严格平衡的二叉搜索树,搜索的时间复杂度为O(log N)。
其次,我们要完成搜索的工作,假设这里搜索5,从根节点出发——[3,8],5比3大,说明p1指向结点的key都比5要小,往右移动,5比8小,则移动到p2所指向的结点——[4,5],5比4大,说明p7指向的子树的key都比5要小,往右移动,等于5,搜索结束。
- 请读者观察B树结点的结构,只是增加了结点中Key的个数,那么结果就会导致整棵树的高度降低,这会导致什么结果呢?
- 举个例子,我们这里把每个结点存放的key再设大一些,设为1024,方便进行比较,那么对于230 个结点,也就是大概10亿结点数,B树的高度就只有3层,而对于红黑树这样的数据结构,高度就为30层左右,两者大致相差27层。
- 这是一个什么概念?要知道数据太多时,内存放不下,甚至就连查找的数据结构都要存放在磁盘当中。那么当进行查找时,就要把结点从磁盘读取出来,这其中要读取多少个结点大致取决于层数,前面我们知道内存的读取速度是磁盘的读取速度的百万倍,那么B树相对红黑树这类平衡二叉树就优化了27层,就相当于优化了2700万倍,这个优化可是很恐怖的!
最后,提一下哈希表这种用空间换时间的数据结构,查找的时间复杂度为O(1),但是当数据越大时,扩容所需的时间也就越长,重要的是当产生冲突时,会导致查找次数增多,进而导致IO次数增多,最终导致查询的效率降低。
2.性质
- 根节点可以为空,否则根节点要么没有孩子,要么至少有两个孩子。
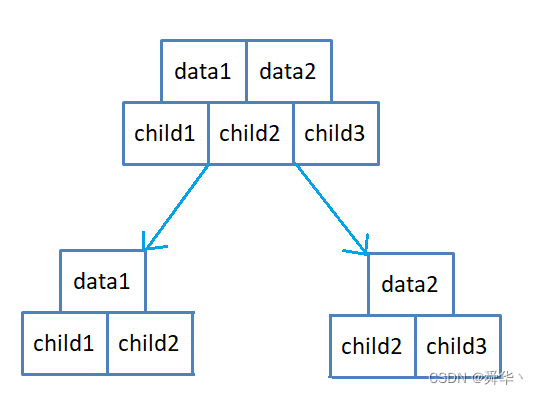
B树在没有插入结点时,即为空树,当根节点满时,再进行插入结点,就要「分裂」,即一分为二,还要生成一个新的根节点会指向新分裂的结点,文字表述太苍白,下面给出一张粗略图解进行说明:
图2:
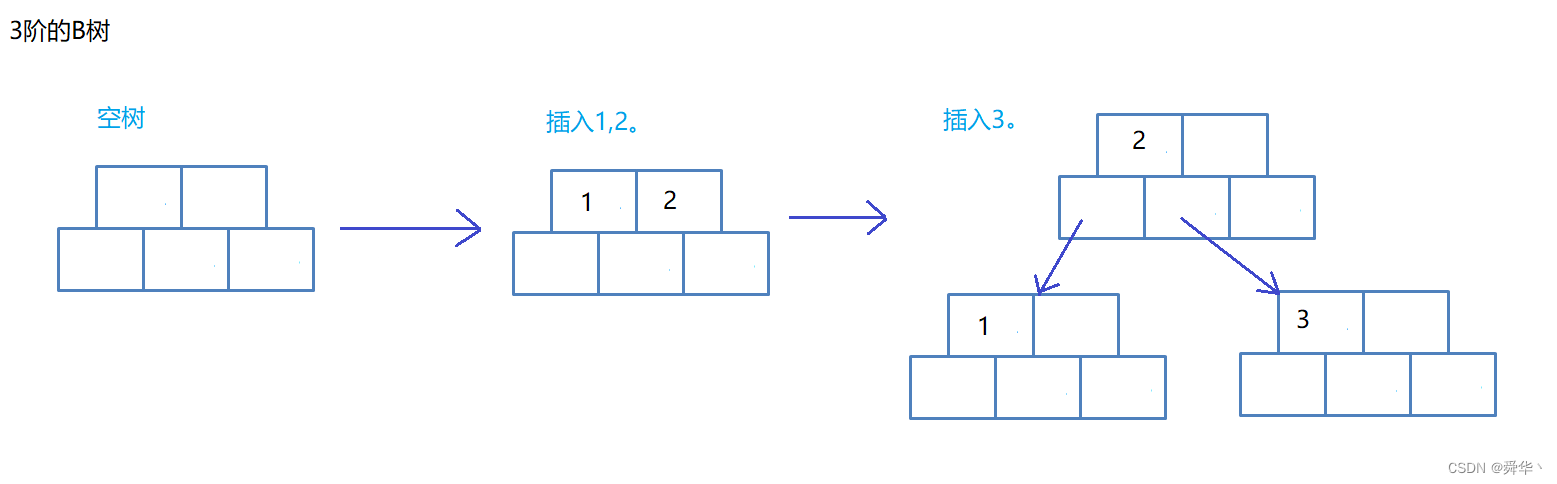
每个分支节点都包含
k-1个关键字和k个孩子,即孩子比关键字多一个,根据此关系进一步理解上一句话,即根节点不为空时至少有两个孩子。每个叶子节点都包含
k-1个关键字。
说明:ceil(M / 2) ≤ k ≤ M,ceil是向上取整函数,请注意这里的k指的是一段范围,而不是具体的某一个数。
图3:
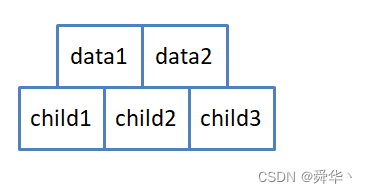
简而言之,孩子比关键字多一个,会有「保底」的效果,比如当在图3中搜索x时,x比data1小的就往child1中,比data1大就往下一个data2,当比data2还大时,且超出范围之后,就往child3指向的结点,其中存放的是比data2还大的数据。简单的说「多个孩子,多条路」。
- 所有的叶子节点都在同一层
这保证了B树是一个绝对平衡的多叉树,即最长路径和最短路径的高度相等,这是由分裂机制保证的,下面的实现部分会对此进行补充。
- 每个节点中的关键字从小到大排列,节点当中k-1个元素正好是k个孩子包含的元素的值域划分。
图4:
对于每个data来说,比如data1的值,划分child1和child2,即child1指向结点的关键码小于data1,child2指向的结点的关键码大于data2,对于data2同样如此,那么把这些结构「去掉重复的,按升序进行合并」就是B树的一个结点。
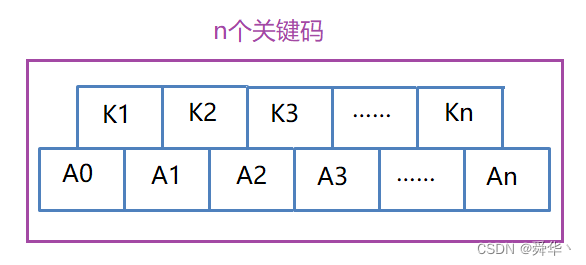
- 每个结点的结构为:(n,A0,K1,A1,K2,A2,… ,Kn,An)其中,Ki(1≤i≤n)为关键字,且Ki<Ki+1(1≤i≤n-1)。Ai(0≤i≤n)为指向子树根结点的指针。且Ai所指子树所有结点中的关键字均小于Ki+1。
结点的结构合并着看,可能有些不好理解,我们先进行分层:
- n,表示的是关键码的个数。
- K1,K2,K3,K4,…… Kn,共计n个关键字
- A0,A1,A2,A3,…… An,共计n + 1个孩子。
图解:
二、实现
1. 插入
说明:
- 此处我们实现的是关键码从小到大排序的。
- 此处关键码我们使用的是唯一的,不允许重复。
- 实现时以3阶B树的插入为例进行讲解。
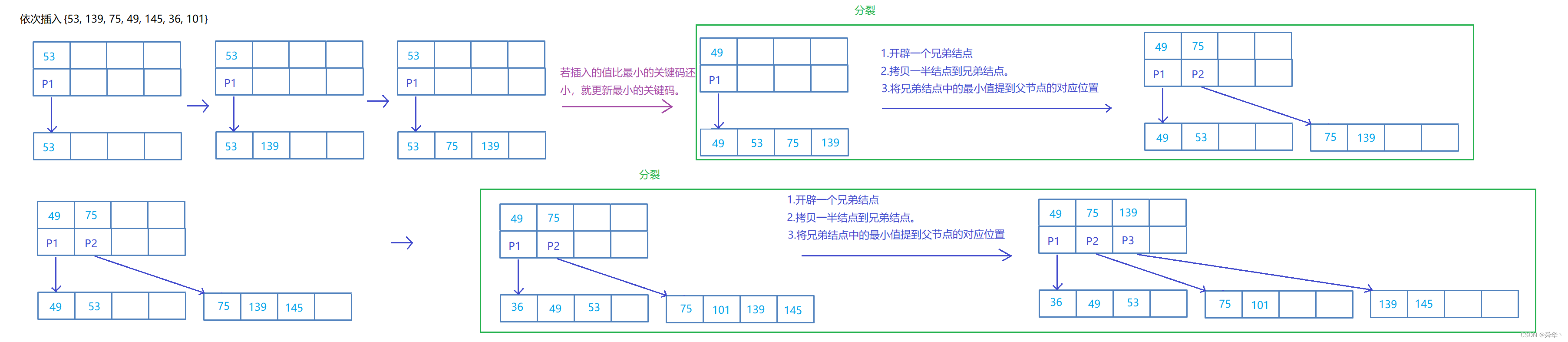
下面我们对3阶的B树依次插入关键码{53, 139, 75, 49, 145, 36, 101},从过程中观察现象得出实现的原理。
首先直观上认为,3阶B树的结点的结构可能是这样的:
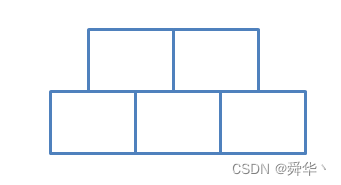
但是经过实践可以得出M阶的B树,在实现代码的过程中都增加一个关键码和孩子指针会降低实现代码的难度。
那么3阶B树的结点这样设计就会更好一点:
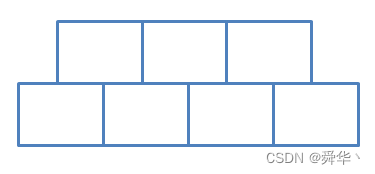
其次,这里可以算出「关键码数目」的最大容量为 max_k == M - 1 = 2,「孩子指针数目」的最大容量为 max_p = M = 3;
下面我们在最初插入结点时,分别使用一下上述两种方式的结点进行实现,进行对比。
- 如果根节点为空,则更新根节点,插入关键码即可。
首先插入53,由于根节点为空,从堆空间开辟一个结点之后存放key,即可。
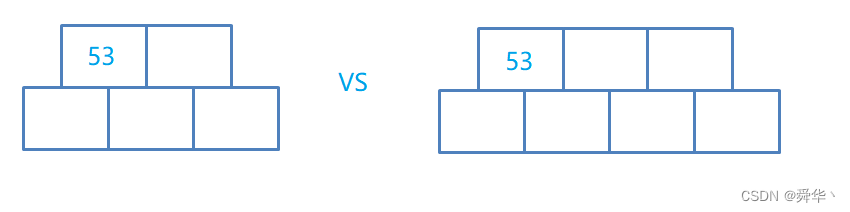
- 结点为根节点,且关键码的个数大于M-1时要进行分裂。
说明:这里M为3,即3阶,每个结点具有三个孩子结点的B树。
其次关键码的个数小于3,我们就继续进行插入{139, 75}
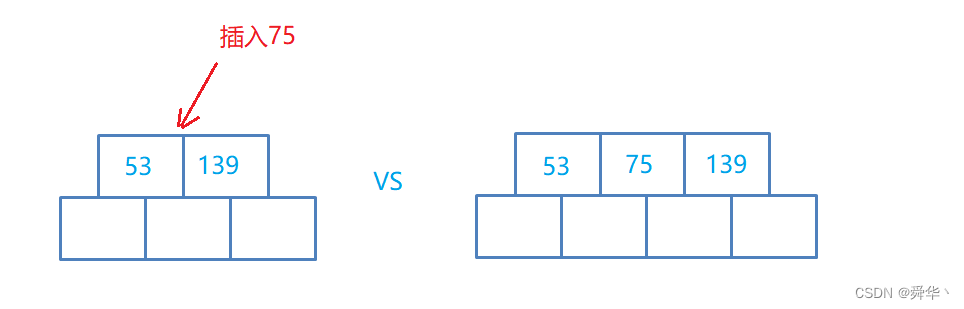
说明:
- 在插入的过程中,要寻找插入关键码的位置,且要将关键码放入其中,那么必然就要挪动关键码,采用的是插入排序的思想实现。
- 对于左边的结点结构来说,插入75时,插不进去了,而且关键码的个数已经达到了最大值2,此处要采用分裂。
- 对于右边的结点结构来说,插入75时,插进去了,且插入后关键码的个数为3大于2,此处要采用分裂。
大致思路:
- 提取结点中间值的key,作为分裂结点的父结点。
- 然后生成一个兄弟结点,将大于key的值拷贝到兄弟结点。
- 父节点指向两个结点,一个是原结点,一个是新生成的兄弟结点。
对于左边的结点进行分裂:
为了方便下面的讨论,此处设x为关键码数组下标 (M - 1)/2指向的值,y为 (M - 1)/2 - 1指向的值。
- x如果小于插入的value,那么x指向的值就是中间关键码。拷贝到兄弟结点的区间为[(M - 1)/2 + 1,M - 1]
- x如果大于插入的value,那么 y可能是中间关键码,如果y小于value,则value是中间关键码反之y是关键码.拷贝到兄弟结点区间为[(M - 1)/2 ,M - 1]。
- 确认中间值的value之后,生成并拷贝原结点的指定区间的关键码到兄弟结点之后。
说明:x等于value就直接返回了,因为本篇讨论的实现不能插入已经存在的关键码。
除此之外还要进行分类讨论:这个指定区间就再上述讨论中产生,这里不再赘述。
- 对于上述第一种情况,那么就在兄弟结点中插入value。
- 对于第二种情况的x大于value的情况,就在原结点插入value。
这一大堆的讨论,在实现时是有亿点点麻烦的,此时我们再来看一看右边的结点。
对于右边的结点进行分裂:
- 设x为(M-1)/2指向的值。
- 直接用x作为父节点的关键码。
- 依次拷贝大于x的值到兄弟结点中。
- 父节点连接原结点和兄弟结点。
右边结点之所以复杂归根到底都是75没插入导致的,那我们多给一个关键码不就行了么,不过我们还要注意关键码与孩子结点的关系,那么这不就是右边的结点结构吗?了解了这一点之后,我们下面就采用右边的这种结点结构继续进行讨论并实现。
最终的结果为:
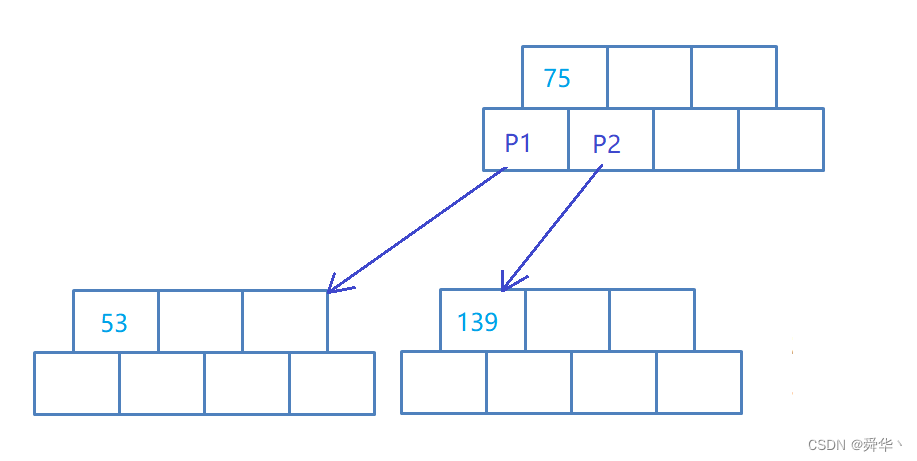
- 插入关键码时,要在指定的「叶子结点」当中插入关键码。
继续插入关键码{49,145}。
- 当插入49时,从根节点的关键码的起始位置进行搜索,这里的75比49要大,那么就要到P1指向的结点中进行搜索,即从53开始搜索,53比49要大,那么就要到空节点了,不能再进行遍历了,因此我们这里要「保存一下每次往下搜索的父结点,最后为空时,最后一次保存的父节点即为插入的叶子结点」。
- 当插入145时,同理,不过这里第一个位置75比145要大,那么就要往右移,不过后面已经没有关键码了,那么我们就要使用最后一个孩子结点,继续进行搜索,同样的我们也可以找到叶子结点。
说明:当找到叶子结点,插入关键码时,可能会挪动数据。
最终的结果:
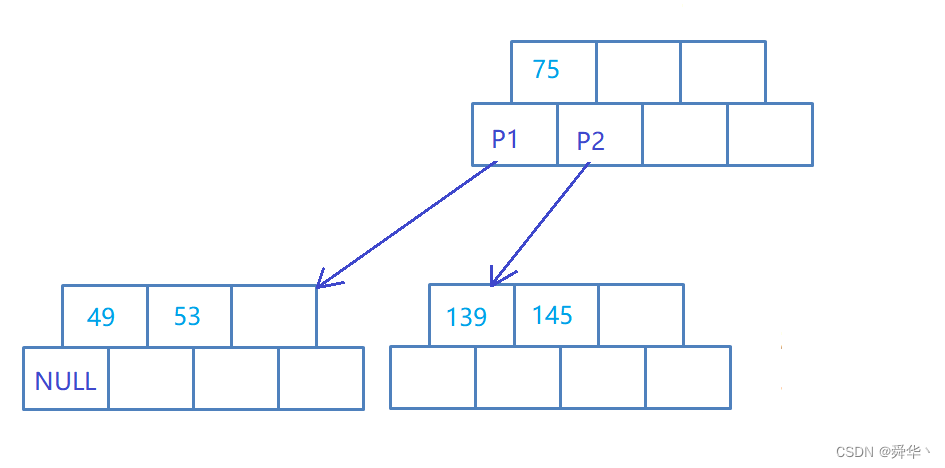
- 叶子结点且不是根节点,其插入前关键码数等于M - 1,且父节点关键码数目小于 M - 1。
说明:此处的M-1为2,M等于3,相当于3阶B树。
继续插入{36}
当关键码的个数满了之后,即提取出「中间关键码」设为「mid」,然后生成一个新的兄弟结点将大于中间关键码的结点拷贝到兄弟结点上,在父节点中插入mid,然后更新孩子的指向。
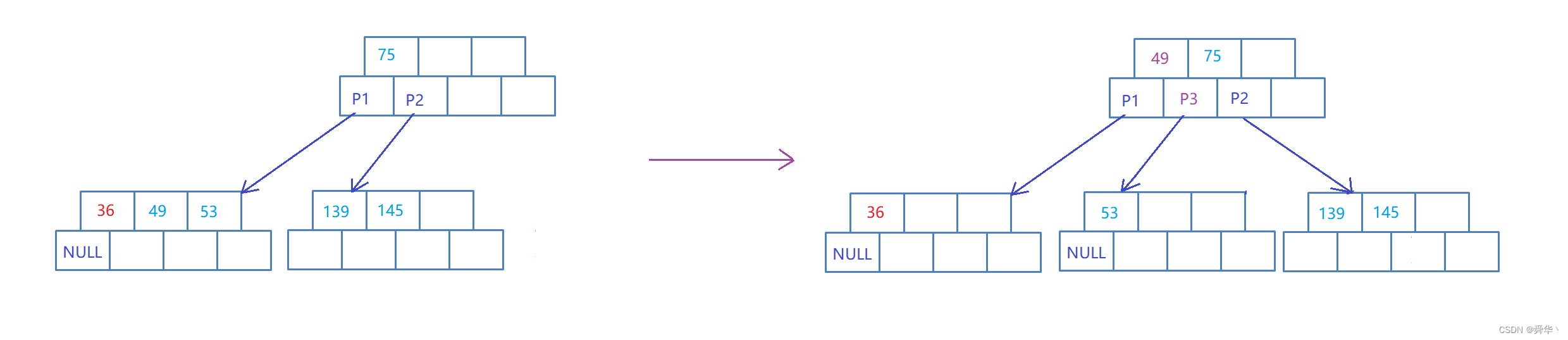
细节:
- 在叶子结点进行分裂时,要将「中间关键码」插入到父亲结点中,因此叶子结点中应要存一个指向父节点的指针,进而找到父节点。
- 设父亲结点中关键码的下标为i,插入「中间关键码」可能要移动位置,而且与之其对应存放指向孩子的指针也要移动位置,即「将下标为i的关键码向后移动时,同时要将下标为 i + 1的孩子指针向后移动」。
至此,可以根据以上的信息,列出实现的基本框架:
#include<iostream>
#include<vector>
template<class K, size_t M>
struct BTNode
{
K _key[M];
BTNode<K,M>* _childs[M + 1];
//这里是为了方便进行实现并保存关键码与孩子指针数目的关系
//无需特判没有位置放的情况,只需判断满或者没满即可。
BTNode<K,M>* _parent;
//当分裂时需要找到父节点,并将分裂的结点链入到父节点。
size_t _size;
BTNode()
:_parent(nullptr), _size(0)
{
for (int i = 0; i < M; i++)
{
_childs[i] = nullptr;
_key[i] = K();
}
//初始化最后一个孩子。
_childs[M] = nullptr;
}
};
template<class K,size_t M>
class BTree
{
typedef BTNode <K, M> Node;
public:
//中序遍历
void _Inorder(Node* root);
void Inorder();
//查找key所在的结点
std::pair<Node*, int> Find(const K& key);
//在cur结点下插入key和node
void InsertKey(Node* cur, const K& key, Node* node);
//插入key,value可以在BTNode设置,此处为了实现方便就不设置了。
bool Insert(const K& key);
//如下是删除实现的相应接口的声明,此处见一见即可。
void EraseKey(Node* node, int pos);
void PopFront(Node* node);
void PushFront(Node* cur, const K& key, Node* brother);
void LeftAdjust(Node* node, Node* parent, int j)
void RightAdjust(Node* node, Node* parent, int pos);
void Merge(Node* lchild, Node* rchild, int pos);
bool Erase(const K& key);
private:
//根节点
Node * _root = nullptr;
};
- 叶子结点且不是根节点,其插入前关键码数等于M - 1,且父节点关键码数目等于 M - 1。
继续插入{101}
与4情况类似,不同的是会导致父节点也会进行分裂:
- 如果父节点不为根节点,那就继续按「情况4」不断讨论处理,直到处理完毕之后结点中的关键码的数目未满。
- 特殊情况,按「情况4」不断处理,如果遇到根节点且关键码满了,此时需要按照「情况2」进行处理。

上述,插入了101之后,进行了一次情况4的处理,以及一次情况2的处理,上文对于情况2的处理最初并不完整,此处再补充一下,即如果根节点如果还有孩子指针,也要将孩子结点拷贝走一半,并将原结点对应的关键码和结点置空。
综上,总共有五种情况的处理,在进行分裂的过程中,上述的分裂机制使B树一般只能横向地分裂结点,保证了同一层分裂的结点高度不会发生变化,而只有到根节点关键码满时,才会进行向上分裂,高度加1。两者共同使B树绝对平衡。
使用例子带各位读者了解插入的情况和具体流程之后,下面进行插入的相应的实现。
首先,当插入关键码时,根结点为空,要开辟新的结点将关键码放进去。
bool Insert(const K& key)
{
if (_root == nullptr)
{
_root = new Node();
_root->_key[0] = key;
_root->_size++;
return true;
}
//......
}
其次,在之后再进行插入关键码时,当关键码不存在时,才能进行插入,否则是不能进行插入的,因此这里要实现查找关键码的操作。
实现细节:
- 当查到关键码Key时,应返回对应关键码的结点,以及关键码所在的下标,以便准确的定位,那么应采用pair<Node*,int>存储。
- 当查不到关键码Key时,应返回关键码应插入的叶子结点,以及用-1表示不存在关键码的下标。
查找思路:
- 当查找关键码Key时,碰到小于Key关键码就继续向右进行查找;
- 找到第一个大于Key的关键码就应该向下查找,这时结点关键码的下标与向下查找孩子结点的下标保持一致。
- 没有大于Key的关键码,就向下查找当前结点的最后一个孩子结点。
- 每次向下更新时,应「保存一下当前结点」,最后当找不到时,即更新到空节点,最终「保存的结点」就是插入关键码的叶子结点。
- 相等时返回指定结点与其对应的下标。
std::pair<Node*, int> Find(const K& key)
{
Node* cur = _root;
Node* parent = nullptr;
while (cur)
{
size_t sz = cur->_size;
int i = 0;
while (i < sz)
{
if (cur->_key[i] > key)
{
break;
}
else if (cur->_key[i] < key)
{
i++;
}
else
{
return std::make_pair(cur, i);
}
}
parent = cur;
cur = cur->_childs[i];
}
return { parent,-1 };
}
实现了查找结点的接口,那么当在插入关键码时,要找一下,如果找到的结点的下标不为 -1,则说明关键码已经存在了,就没必要进行插入了,如下是这一部分的实现代码,承接上面的插入代码。
bool Insert(const K& key)
{
//1.根节点为空,详见上文
//2.查找Key值是否存在
//2.1.Key值存在
std::pair<Node*, int> pa = Find(key);
if (pa.second != -1)
{
//说明已经存在
return false;
}
//......
}
当进行插入时,首先可以将关键码直接插入在对应叶子结点中,然后再判断是否要进行分裂,那这一段逻辑可以封装成接口的形式进行呈现。
void InsertKey(Node* cur, const K& key)
{
int end = cur->_size - 1;
while (end >= 0)
{
if (cur->_key[end] > key)
{
//向右移动关键码
cur->_key[end + 1] = cur->_key[end];
//更新end
end--;
}
else
{
break;
}
}
cur->_key[end + 1] = key;
cur->_size++;
}
除此之外,应还有考虑到第四种情况,即在分支结点上插入key和新分裂的孩子结点,那么孩子结点也要进行移动,即将「下标为i的关键码向后移动一个位置时,同时要将下标为 i + 1的孩子指针向后移动一个位置」。
综合上述两种情况,实现的插入的逻辑应该是这样的:
void InsertKey(Node* cur, const K& key,Node* brother)
{
int end = cur->_size - 1;
while (end >= 0)
{
if (cur->_key[end] > key)
{
//向右移动关键码和孩子
cur->_key[end + 1] = cur->_key[end];
cur->_childs[end + 2] = cur->_childs[end + 1];
//更新end
end--;
}
else
{
break;
}
}
cur->_key[end + 1] = key;
cur->_key[end + 2] = brother;
cur->_size++;
}
当为叶子结点时,brother参数设置为空即可,下面接着回归到Insert的逻辑,即将key插入到叶子结点中。
bool Insert(const K& key)
{
//1.根节点为空,详见上文
//2.查找Key值是否存在
std::pair<Node*, int> pa = Find(key);
//2.1.Key值存在
//...
//2.2.Key值不存在
Node* cur = pa.first;
Node* brother = nullptr;
K newkey = key;
//将newkey插入到cur叶子结点当中
InsertKey(cur, newkey, brother);
//然后对结点Key的数量进行判断
if (cur->_size <= M - 1) //关键码的最大数量为M - 1。
{
//说明没满,返回true即可
return true;
}
//....
}
- 当关键码的数量大于 M - 1时,就该分裂了,但是分裂的情况可能会一直持续,因此处理的方向是一个循环,且分裂时处理模式为「将中间关键码」和「新分裂的兄弟结点」插入到「父节点」中,此对叶子结点通用,即将「中间关键码」和「空节点」插入到「叶子节点」。
- 此时插入之后就要考虑父节点的关键码的数量满没满的情况,如果没满循环结束,否则就要继续向上进行分裂。
- 父节点为根节点且关键码满时,需要特殊处理,即更新根结点,用于存放中间关键码,以及执行「原根节点」和「分裂的结点」,具体参考情况2,4,5对应图解进行理解。
实现如下:
bool Insert(const K& key)
{
std::pair<Node*, int> pa = Find(key);
if (pa.second != -1)
{
//说明已经存在
return false;
}
Node* cur = pa.first;
Node* brother = nullptr;
K newkey = key;
//插入实现的核心逻辑:
while (1)
{
//将newkey插入到cur叶子结点当中
InsertKey(cur, newkey, brother);
//然后对结点Key的数量进行判断
if (cur->_size <= M - 1) //关键码的最大数量为M - 1。
{
//说明没满,返回true即可
return true;
}
int sz = cur->_size;
//分裂出一个结点
brother = new Node;
//提取出中间关键字
int mid_index = sz / 2;
K midkey = cur->_key[mid_index];
int j = 0;
for (int i = mid_index + 1; i < sz; i++,j++)
{
//拷贝关键码和孩子结点到brother
Node* node = cur->_childs[i];
brother->_key[j] = cur->_key[i];
brother->_childs[j] = node;
//别忘了更新孩子结点的父节点的指向
if (node) node->_parent = brother;
//更新brother的关键码的数目大小
brother->_size++;
}
//最后一个孩子也要进行拷贝,别忘了孩子结点比关键码的数目多一个
Node* node = cur->_childs[sz];
brother->_childs[j] = node;
if (node) node->_parent = brother;
//更新cur的关键码的数目大小
cur->_size -= (brother->_size + 1);
//这里的1是提取出来的中间关键码
//最终先特判是否为根节点
if (cur == _root)
{
//更新根节点和连接关系
_root = new Node;
_root->_key[0] = midkey;
_root->_childs[0] = cur;
_root->_childs[1] = brother;
//别忘了让孩子也指向根节点
cur->_parent = brother->_parent = _root;
//更新根节点的关键码数目
_root->_size++;
break;
}
else
{
//转换为在cur父节点插入brother结点和newkey。
newkey = midkey;
cur = cur->_parent;
//别忘了让新开辟的bro孩子也指向父节点
brother->_parent = cur;
}
}
return true;
}
在插入写完都没有报错之后,可以编写一个中序遍历进行测试,若为升序则大概率说明插入实现成功。
void _Inorder(Node* root)
{
if (root == nullptr)
{
return;
}
//左-根-左-根-右。
for (int i = 0; i < root->_size; i++)
{
_Inorder(root->_childs[i]);
std::cout << root->_key[i] << " ";
}
//右
_Inorder(root->_childs[root->_size]);
}
void Inorder()
{
_Inorder(_root);
}
2. 删除
- B树的删除,博主觉得还是有不少难度的,如果有兴趣可以试着钻研一下,如果没有兴趣,可跳过此内容,了解插入即可。
删除思路,跟所有搜索二叉树的思路大同小异:
- 如果要删除的是叶子结点,那么就执行删除逻辑。
- 如果要删除的不是叶子结点,那么就寻找到左子树的最大结点或者右子树的最小结点,进行交换,然后转换为第一种情况。
- 删除完关键码之后,使树的状态更新到符合其定义为止。
对第1,2情况的处理代码如下:
bool Erase(const K& key)
{
//首先删除key,得有key
std::pair<Node*, int> pa = Find(key);
if (pa.second == -1)
{
//说明没有,返回false
return false;
}
//其次与搜索树的删除的大框架类似,首先要找到左子树的最大值或者右子树的最小值,然后进行替换。
//将问题转换将删除分支结点转换为叶子结点,此处采用替换「右子树的最小值」。
Node* cur = pa.first;
int pos = pa.second;
//找到右边的孩子结点。
Node* rnode = cur->_childs[pos + 1];
if (rnode != nullptr)//说明是非空结点
{
//找到右子树的最小值进行替换
Node* parent = cur;
while (rnode)
{
parent = rnode;
rnode = rnode->_childs[0];
}
//替换掉cur的key
cur->_key[pos] = parent->_key[0];
//更新cur,pos
cur = parent;
pos = 0;
}
//直接将关键码移除,即将pos之后的关键码和孩子结点往前移一位。
EraseKey(cur, pos);
//...
//更新情况
}
void EraseKey(Node* node, int pos)
{
size_t& sz = node->_size;
//往前移一位
for (int n = pos + 1; n <= sz; n++)
{
node->_key[n - 1] = node->_key[n];
node->_childs[n] = node->_childs[n + 1];
//清空一下
node->_key[n] = K();
node->_childs[n + 1] = nullptr;
}
sz--;
}
如下进行更新状态的分类讨论:
首先结点关键码的个数为 K - 1,ceil(M / 2) <= K <= M,ceil为上取整函数,可以得出结点关键码个数的最小值为 ceil(M / 2) - 1,此处设为「minkey」,当M为3时,最小值为1,那也就意味着对于3阶的B树,只要关键码的个数大于0,就无需进行调整,否则就要进行调整。
-
如果删除之后,关键码的个数大于等于「minkey」不做调整直接返回即可。
-
删除之后,关键码的个数小于「minkey」那么就要执行操作,使之保持B树的性质。操作主要涉及两个动作,「移动关键码和孩子」和「合并」。
那么接着对小于minkey的关键码的结点执行的操作进一步进行分析:
- 如果有左孩子。
- 其关键码的个数大于「minkey」,那么就「移动关键码和孩子」,并进行调整。
- 其关键码的个数小于 「minkey」,那么就 「合并结点」到左孩子上,并进行调整。
图解:

实现代码:
void PushFront(Node* cur, const K& key, Node* brother)
{
int end = cur->_size;
while (end >= 0)
{
//向右移动关键码和孩子
cur->_key[end + 1] = cur->_key[end];
cur->_childs[end + 2] = cur->_childs[end + 1];
end--;
}
//把第一个孩子再往后移动。
cur->_childs[end + 2] = cur->_childs[end + 1];
cur->_key[0] = key;
cur->_childs[0] = brother;
cur->_size++;
}
void RightAdjust(Node* node, Node* parent, int pos)
{
Node* brother = parent->_childs[pos];
int min_num = (M + 1) / 2 - 1;
size_t& bsz = brother->_size;
if (bsz > min_num)
{
size_t& nsz = node->_size;
//此处先保存一下,下面跟结点一块插入node中。
K key = parent->_key[pos];
//将brother最大的关键码提到父节点的对应位置
parent->_key[pos] = brother->_key[bsz - 1];
//将brother的最后一个指针插入到node的中
Node* child = brother->_childs[bsz];
//更改孩子结点的指向。
if (child)child->_parent = node;
PushFront(node, key, child);
//清空一下brother中的拷贝结点与key
brother->_childs[bsz] = nullptr;
brother->_key[bsz - 1] = K();
//更新brother的sz
bsz--;
}
else
{
Merge(brother, node, pos);
}
}
- 如果没有左孩子,就找右孩子。
- 其关键码的个数大于「minkey」,那么就「移动关键码和孩子」,并进行调整。
- 其关键码的个数小于 「minkey」,那么就 「合并结点」到左孩子上,并进行调整。
图解:

实现代码:
void PopFront(Node* node)
{
size_t& sz = node->_size;
//往前移一位
for (int n = 1; n <= sz; n++)
{
node->_key[n - 1] = node->_key[n];
node->_childs[n - 1] = node->_childs[n];
//清空一下
node->_key[n] = K();
node->_childs[n] = nullptr;
}
node->_childs[sz] = node->_childs[sz + 1];
node->_childs[sz + 1] = nullptr;
sz--;
}
void LeftAdjust(Node* node, Node* parent, int j)
{
Node* brother = parent->_childs[j + 1];
int min_num = (M + 1) / 2 - 1;
if (brother->_size > min_num)
{
size_t& nsz = node->_size;
//将父节点的对应位置的关键码移到node中
node->_key[nsz] = parent->_key[j];
nsz++;
//然后将brother中最小的结点提上去
parent->_key[j] = brother->_key[0];
//然后将brother的最左边的孩子结点移到node的最后一个位置上
node->_childs[nsz] = brother->_childs[0];
//别忘了更改孩子结点的父节点的指向
Node* child = brother->_childs[0];
if (child) child->_parent = node;
//然后将brother的后面的关键码和指针往前移动。
PopFront(brother);
}
else
{
//将兄弟结点进行合并
Merge(node, brother, j);
}
}
最后,两种方法都有合并的操作,那么为了降低代码的耦合度,对合并操作单独实现。
void Merge(Node* lchild, Node* rchild, int pos)
{
Node* parent = lchild->_parent;
//将右孩子的关键码和指针拷到左孩子上
int lsz = lchild->_size,rsz = rchild->_size;
int j = lsz;
//首先将父节点的j位置的关键码拷贝下来。
lchild->_key[j++] = parent->_key[pos];
for (int i = 0; i < rsz; i++, j++)
{
//拷贝右孩子到左孩子上
Node* node = rchild->_childs[i];
lchild->_key[j] = rchild->_key[i];
lchild->_childs[j] = node;
//别忘了更改孩子父节点的指向
if (node) node->_parent = lchild;
}
//拷贝rchild的最后一个孩子并更改孩子指向。
Node* node = rchild->_childs[rsz];
lchild->_childs[j] = node;
if (node) node->_parent = lchild;
//更新lchild的size
lchild->_size += (rsz + 1);
//1指的是从父节点拷贝下来的关键码
//将父节点的pos位置的关键码删除,即向前移动覆盖
EraseKey(parent, pos);
//最后将rchild结点进行删除
delete rchild;
}
补充:插入的生长方向是向右生长和向上生长,删除的生长方向就要逆着来,即向左退缩和向下退缩。
下面讨论特殊的情况:
- 可能会遇到调整之后,由于进行了合并操作,从父节点中顺下了一个关键码,那么就有可能导致父节点的关键码的个数小于minkey,此时就要转换为对父节点进行调整操作,操作同上述两种情况。那么此时就是一个不断向上循环的过程。
- 父节点为根节点,且关键码的个数小于minkey但大于0,无需对父节点再进行操作,直接终止循环返回即可。
- 父节点为根节点,且关键码的个数等于0,需要释放并更新父节点为最左边的孩子,返回即可。
由于1,2情况比较好理解,可简单画图和借助上述两种情况进一步分析,此处只对情况3进行图解的补充:

讨论完毕,对删除中更新的逻辑做一下整体的概括,即如果关键码的个数小于min_num且结点不为根节点,就分类讨论进行更新,更新完毕之后将结点赋值为父结点;否则终止循环;循环执行上述逻辑。循环结束之后对特殊情况3进行特判。
实现代码:
bool Erase(const K& key)
{
//执行查找与删除的逻辑此处省略,详见上文。
//.....
//执行处理平衡的逻辑。
int min_num = (M + 1) / 2 - 1;
//关键码的范围为:大于等于 ceil(M / 2) - 1,ceil为上取整函数。
while (1)
{
int sz = cur->_size;
if (sz >= min_num)
{
return true;
}
//说明需要进行调整关系,进而保证是一棵B树。
//先找到父节点对应cur的位置。
int j = 0;
Node* parent = cur->_parent;
//特判
if (parent == nullptr)
{
//说明cur是根节点。
break;
}
int end = parent->_size;
for (; j <= end; j++)
{
if (parent->_childs[j] == cur)
{
break;
}
}
//其次分类进行讨论
if (j == 0)
{
//找cur的右兄弟进行调整关系,移动key到左边
LeftAdjust(cur,parent,j);
}
else
{
//找cur的左兄弟调整关系,移动key到右边
RightAdjust(cur, parent, j - 1);
}
//向上进行遍历
cur = parent;
}
if (cur == _root && cur->_size == 0)
{
Node* delnode = _root;
_root = delnode->_childs[0];
delete delnode;
//更改父节点的指向,前提是根节点不为空。
if (_root)
{
_root->_parent = nullptr;
}
}
return true;
}
3. 测试
上述内容只是针对性地呈现代码,并不全,若要进行测试,还请看博主Gitee有详细的源码,点击蓝色的链接即可进入。
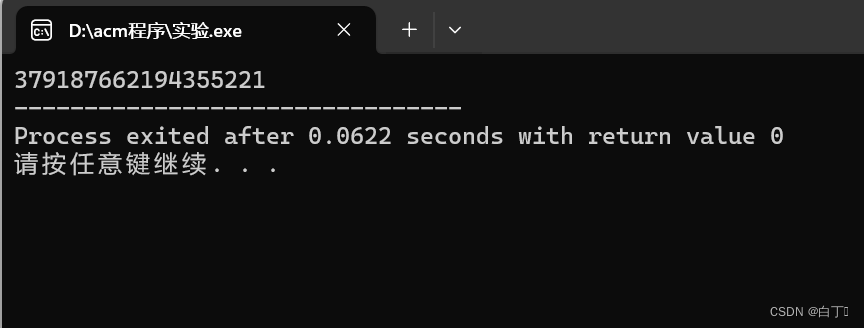
此处使用一百万个随机值进行测试,如果退出码正常,即为0,则表明实现的基本无误。
const size_t M = 3;
void Test()
{
BTree<int, M> btree;
std::vector<int> arr;
//插入大约十万个随机值进行测试。
srand(time(nullptr));
for (int i = 0; i < 100000; i++)
{
int num = rand();
arr.push_back(num);
}
for (auto num : arr)
{
btree.Insert(num);
}
for (auto num : arr)
{
btree.Erase(num);
}
}
结果:
三、拓展
1. 23查找树
- 定义:2-3查找树是一种自平衡的二叉查找树,用于在计算机科学中进行数据存储和检索。它的名称表明,每个节点可以存储1个、2个或3个关键字,并且具有2个、3个或4个子节点。2-3查找树的设计旨在保持树的平衡,以确保检索操作的高效性。
了解前面的B树,再来看所谓的23查找树,其实就是一颗3阶的B树,上述的博主画的所有图解,都可以借助着去理解23查找树的插入和删除,此处不再赘述。不过值得注意的是,23查找树和B树都是由Rudolf Bayer和Edward M. McCreight都在1972年被提出,可见两者真是同根同源,不仅如此,这俩大佬还发明了红黑树。
2. B+树
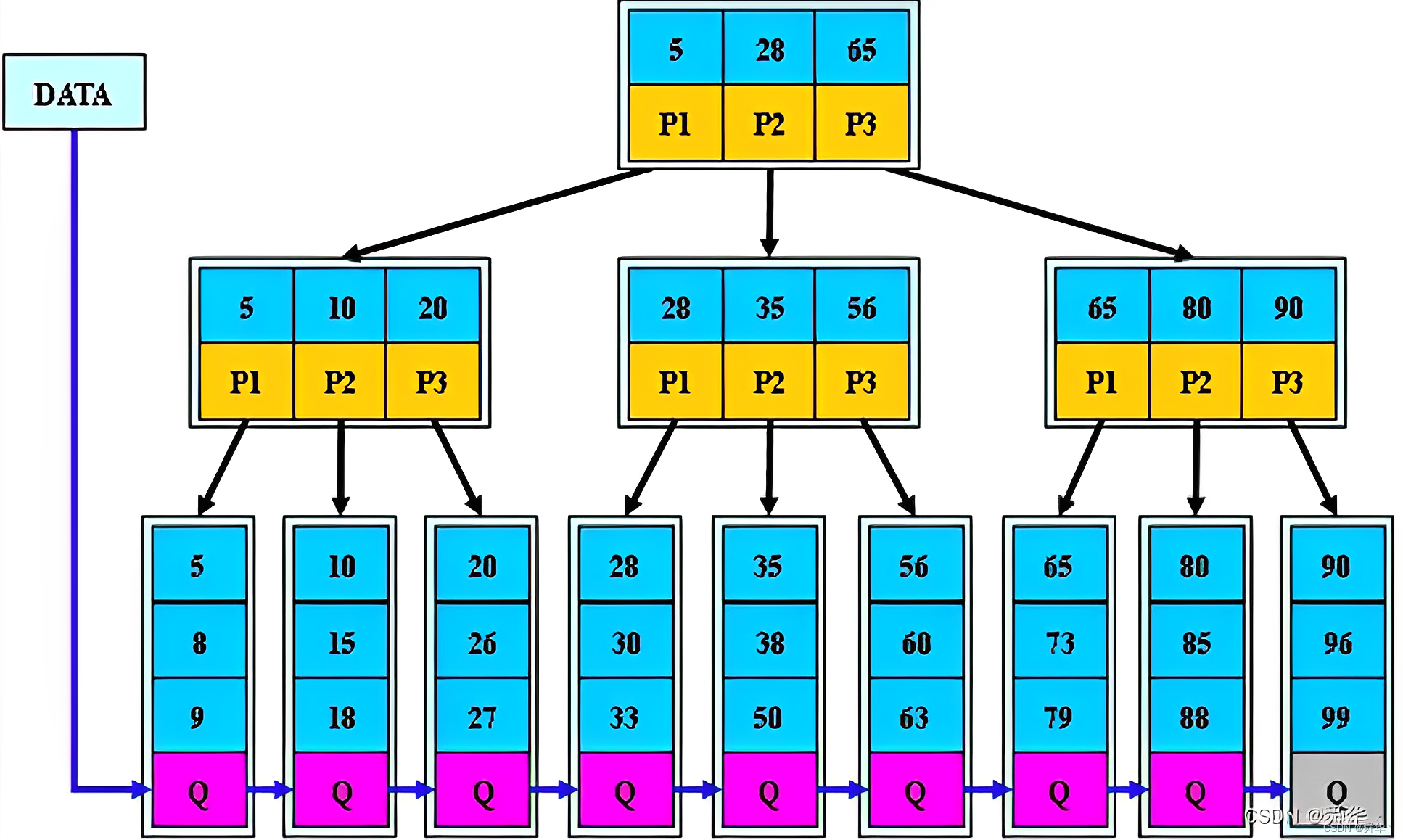
概念:整体上与B树相似,但是做了以下几点优化,更便于查找。
- 分支节点的子树指针与关键字个数相同。
- 分支节点的子树指针p[i]指向关键字值大小在
[k[i],k[i+1])区间之间。 - 所有叶子节点增加一个链接指针链接在一起。即叶子结点遍历可以取到所有的值。
- 所有关键字及其映射数据都在叶子节点出现。
性质:
- 所有关键字都出现在叶子节点的链表中,且链表中的节点都是有序的。
- 不可能在分支节点中命中,分支节点只充当索引。
- 分支节点相当于是叶子节点的索引,叶子节点才是存储数据的数据层。
图解:
简单模拟插入流程:
总体上优化可以概括为:
- 调整结点中关键码的个数与孩子的个数对应,调整搜索的关系,相比较B树代码实现难度有所降低。
- 分支结点中存放的只是索引,即所有的数据都在叶子结点中,分支结点只是部分的数据充当索引,在一定程度上降低了树的高度。
- 对数据的遍历改为将叶子结点以链表的形式串起来,相比于B树中序遍历来说,遍历较为直接和方便。
说明:B树相较于B+树,值可以在分支结点中进行读取,而B+树必须要到叶子结点中才能读取,这是B树的优势。
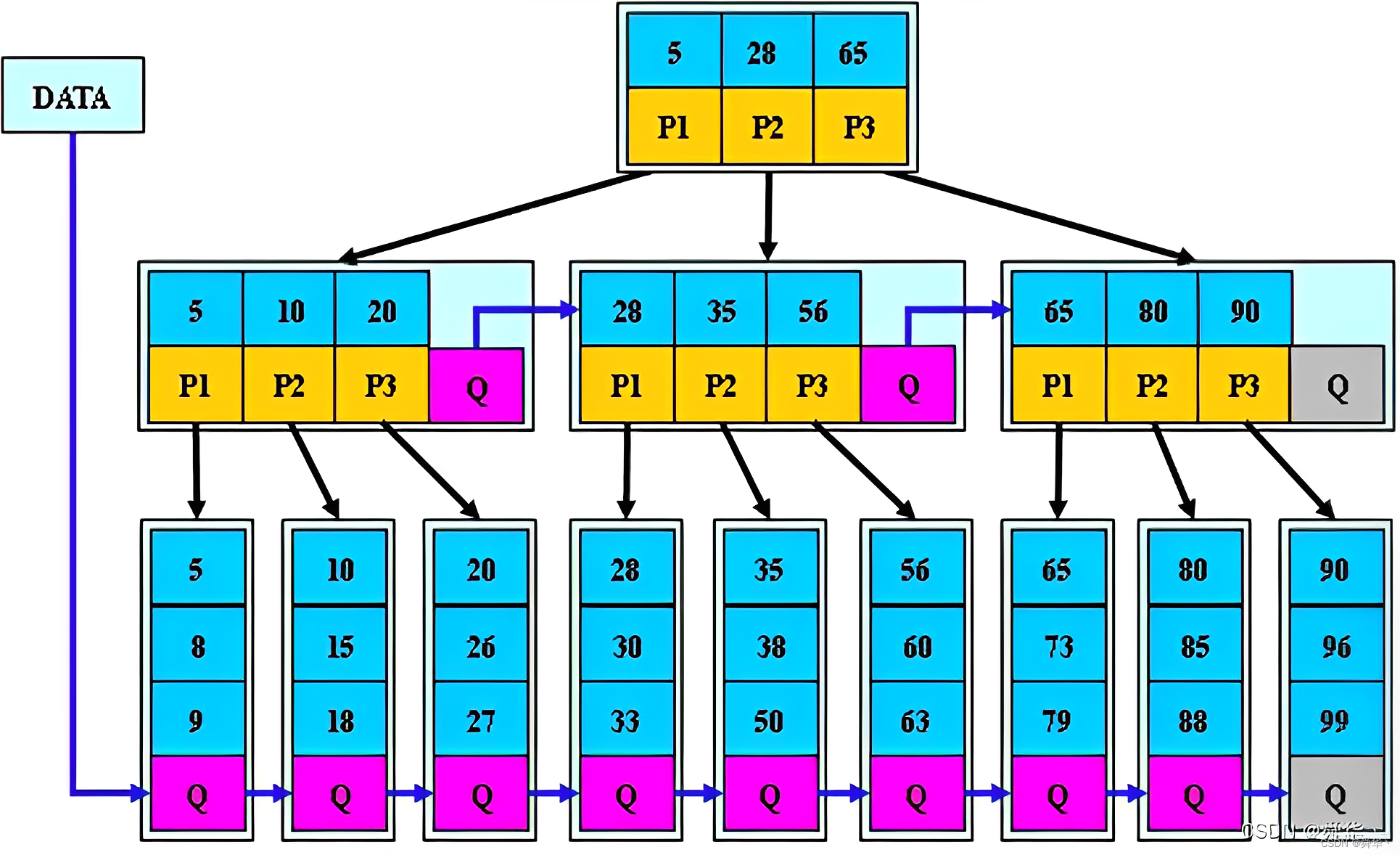
3. B*树
概念:与B+树整体类似,但做了几点小优化,进而提高空间的利用率。
- 同一层的分支结点用指针进行串联。
- 在分裂时,如果结点满了需要分裂,先看兄弟结点是否满了,如果没满,那就将结点移至兄弟结点,如果满了,那就各拷贝当前结点和兄弟结点的三分之一到新生成的分裂结点,链入到其父节点对应的位置当中。
图解:
简单模拟插入流程:

总的来说,通过利用兄弟结点的关键码的空闲位置,降低分裂结点的频率,进而提高空间的利用率。
最后来小小的总结一下:
虽然B树系列在磁盘当中的优势很大,但是在内存中相比哈希,二叉平衡搜索树,B树系列存在:
- 空间利用率相对较低,消耗高,因为结点总会有没满的情况,满了就要分裂。
- 插入删除时,要挪动数据,也会消耗性能。
- 高度虽然更低,但是在内存中进行查找差别不大。
因此,B树系列的数据结构在内存中体现不出优势,磁盘才是B树系列的主场。
4. MySQL
要了解MySQL,先要知道数据库——简单来讲就是存储在磁盘中大量结构化数据,那么MySQL就是一种数据库服务,即用来增删查改数据库中数据的服务。
那当在磁盘中进行增删查改时,几乎都要先找到数据,那么使用B树系列(一般为B+树)或者哈希等数据结构管理和查找数据,方便增删查改就很有必要了,这类方便进行在数据库中高效进行查找的数据结构,一般被称之为索引,换句话「数据库中索引是数据结构」,更进一步「B树系列可以充当数据库的索引」。
为啥要说MySQL这种数据库服务呢?其实很简单免费,开源,效率高。
结构图解:
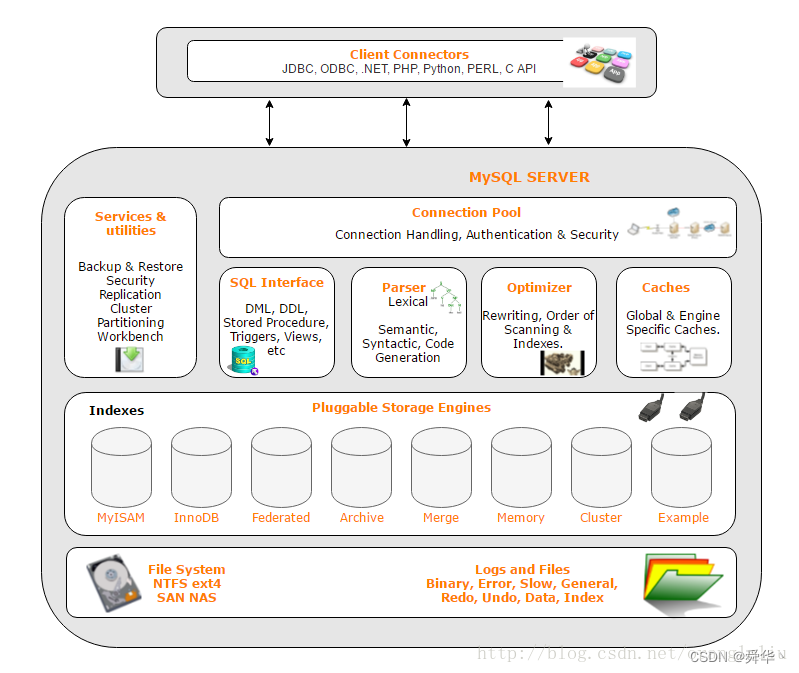
图中的存储引擎,即Storage Engines,一大堆的存储引擎其实就是对索引的不同实现方案,用以满足不同的场景需求,下面介绍两种常见的存储引擎MyISAM和InnoDB。
正式介绍之前,先来铺垫一些概念,方便之后进行叙述:
- 主键,简单来说就是B树系列的关键码,用于查找,不允许重复。
- 辅键,相对于主键来说,允许重复。
- 非聚集索引,简单来说就是索引文件和数据文件分开进行存储。
- 聚集索引,索引文件和数据文件一块存储。
- 事务,对数据库进行的操作,保证原子性,一致性, 隔离性,持久性,简称ACID。
- MyISAM,MySQL5.5.8版本之前默认的存储引擎,不支持事务,采用非聚集索引。
使用此结构,举一个例子:
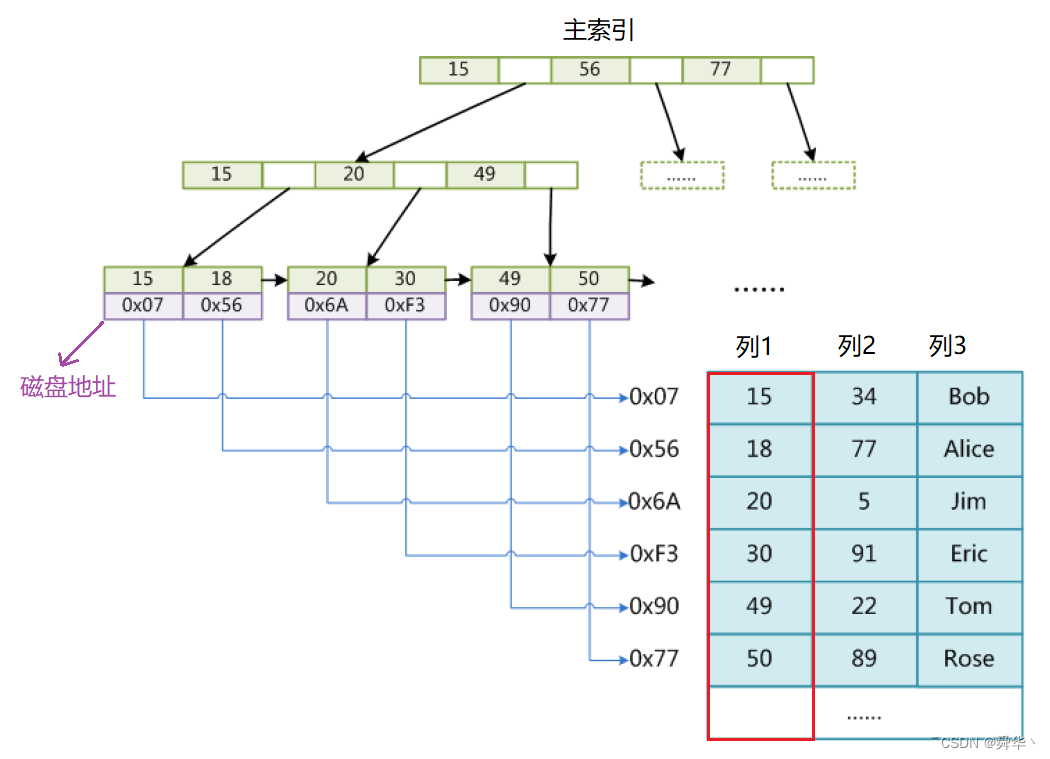
- 首先,此处采用列1作为主索引,即主键,要求不允许重复,采用的索引结构是B+树的。
- 其次,键值对应的值为地址,即对应数据表中所在行的的地址,需注意此处地址都为磁盘地址。
- 最后,索引文件和数据文件分离,即B+树的索引文件和表文件是分开的,也就是所谓的非聚集索引。
如果要使用辅助索引,即辅键,可以重复,再建立一个索引文件呢? 下面使用列2作为辅键建立索引文件。
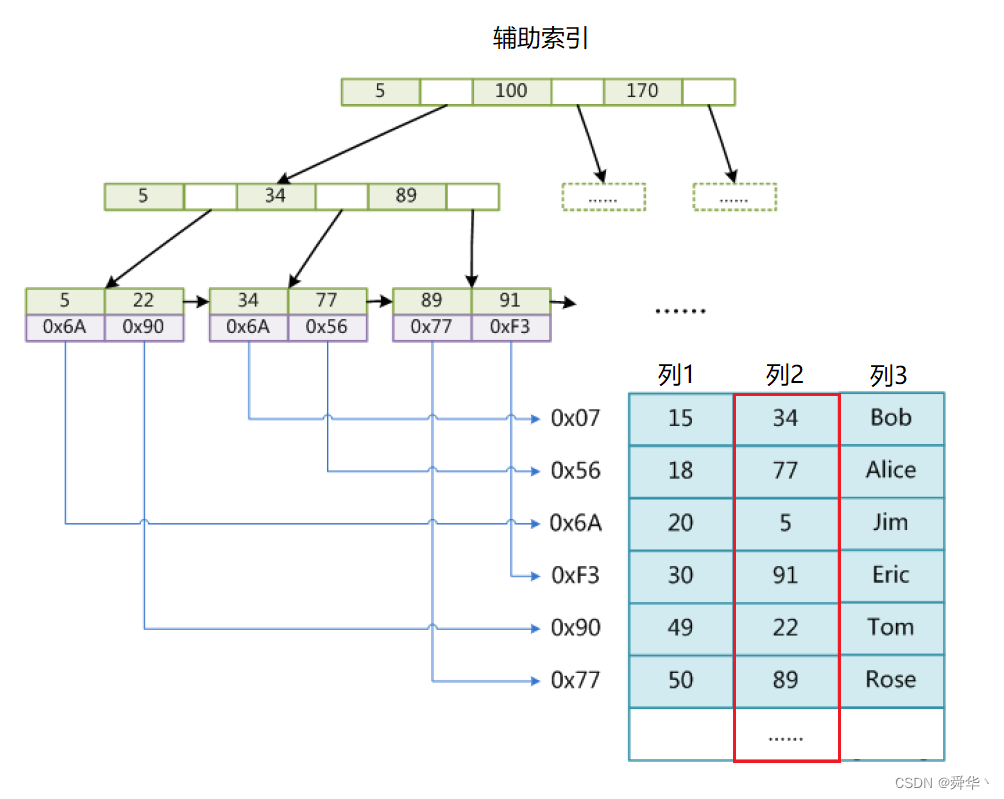
这里就会有一个小疑问,即如果使用重复的辅键进行搜索,是会将显示所有的相同辅键的搜索结果,还是会报错呢?答案是报错,即不允许搜索时,出现二义性,保证结果唯一。
- InnoDB,MySQL数据库5.5.8版本开始,默认的存储引擎,支持事务,采用聚集索引。
使用此结构举一个例子:
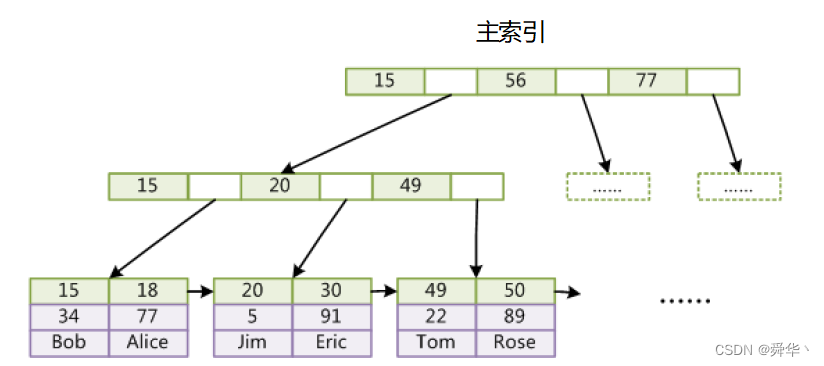
- 首先,索引文件和数据文件合而为一,即无需再通过叶子结点找到对应数据的磁盘地址再进行索引,即聚集索引。
- 其次,相比较非聚集索引,相同内容,少在磁盘IO一次,因此效率相比之下是较高的。
这里就有一个问题,如何建立辅助索引呢?设计者实现的就很巧妙,即将叶子结点中的值换成主键。
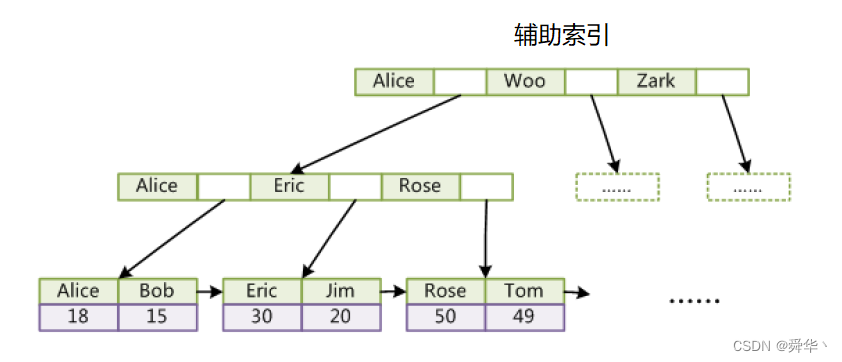
那么通过辅键找到主键,再通过主键进行索引,即可找到对应的数据,也就是进行两次查找。
总结
本篇文章从B树出发,了解其概念,性质,并穿插实现了查找,插入,删除,并进行了测试保证代码的正确性,最后简单地拓展了23查找树,B+树,B树,以及实际采用对应数据结构的一种数据库服务MySQL。总的来说,希望读者能够在看完这一篇文章之后心里有点 “B树”,hhh。
我是舜华,期待与你的下一次相遇!
![[JNI]使用jni实现简单的Java调用本地C语言代码](https://img-blog.csdnimg.cn/direct/b1a2c2ef448c44a5951dadc5696a33ed.png#pic_center)