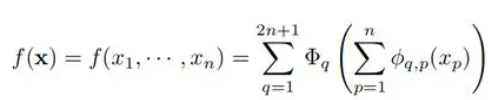二叉搜索数使用,底层原理及代码实现

news2024/11/27 18:50:34

1:二叉搜索树的定义

二叉搜索树的底层是一个二叉链表

二叉搜索树又称二叉排序树，它或者是一棵空树 ，或者是具有以下性质的二叉树 :
  1. 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
  2. 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
  3. 它的左右子树也分别为二叉搜索树

举个例子,我们要把数组[50,87,64,100,24,35,1,77]插入到二叉搜索树中,对应的树应该是这个样子

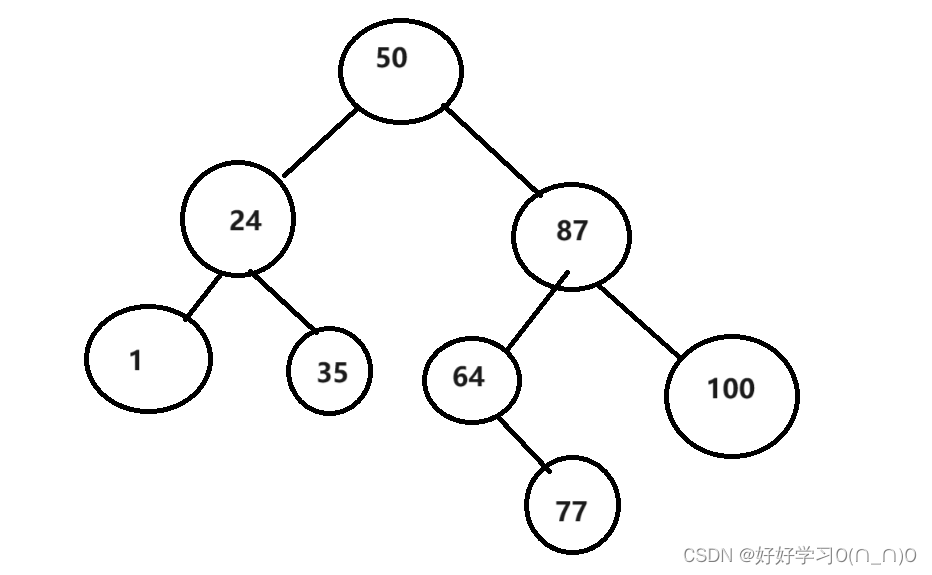
2.二叉搜索树的特点

  1. 既然以搜索树为名字,显然搜索功能是很强大的(相较于数组的搜索),对于二叉树的每一个节点来说其左子树的任意值绝对小于根节点,右子树的任意值绝对大于根节点,如果我们要查找一个值,该值比根节点小的话去左子树找,比根节点大的话去右子树找,如果二叉搜索树是一颗满二叉树的话,搜索的时间复杂度将为log(N),相当于从全世界70亿人中找一个人仅用了30次操作.
  2. 因为二叉树的左子树的任意值绝对小于根节点,右子树的任意值绝对大于根节点,所以其中序遍历即为升序数组,搜索树理论上不可以同时存在多个相同的元素,因为这是没有意义的,所以严格来说,这是一个无重复元素的升序数组

3.二叉搜索树的底层原理

插入

显然原树在执行完插入操作后仍应该是二叉搜索树,为了不破坏原树的结构,对于根节点来说,如果插入值大于根节点,应该往右插入,插入值小于根节点,应该往左插入.直到最后1.找到的节点为空,代表应该向空节点处插入2.存在节点值 == 插入值,这样的插入是无意义的,插入失败!

以上图为例,如果要插入一个76

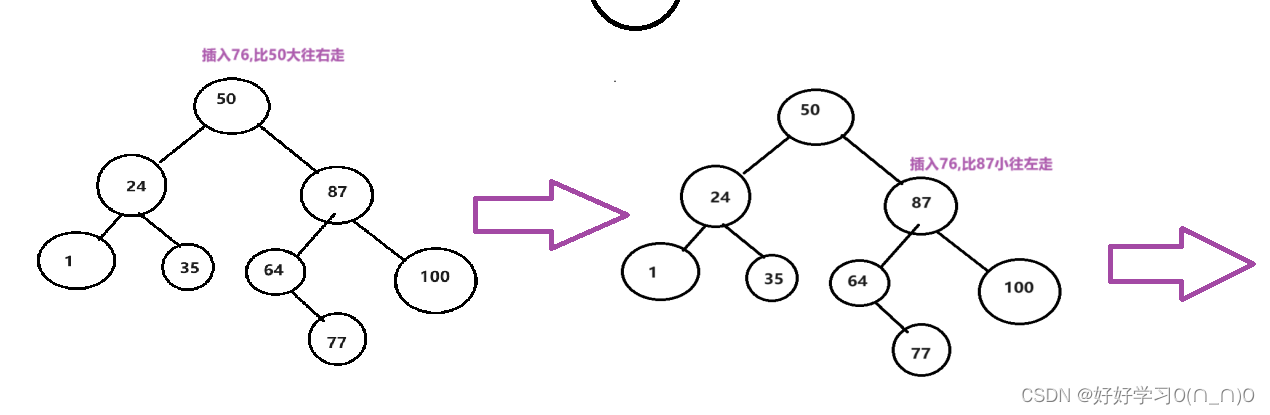
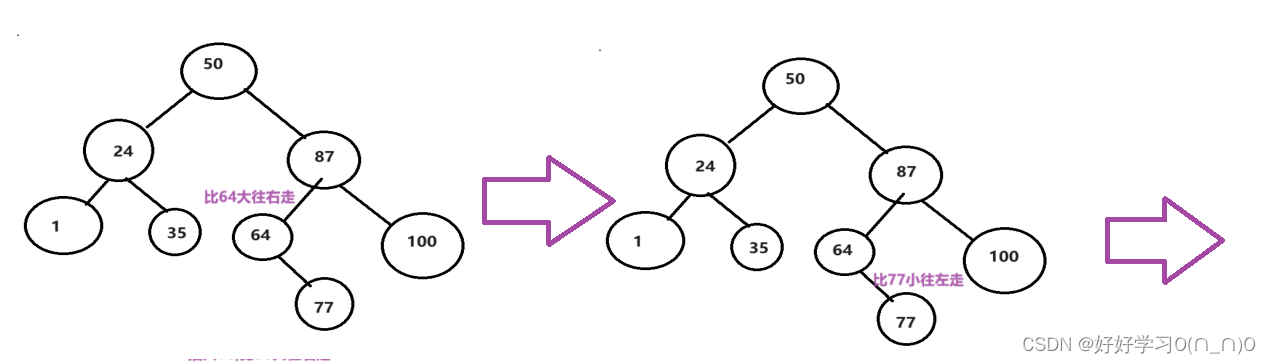
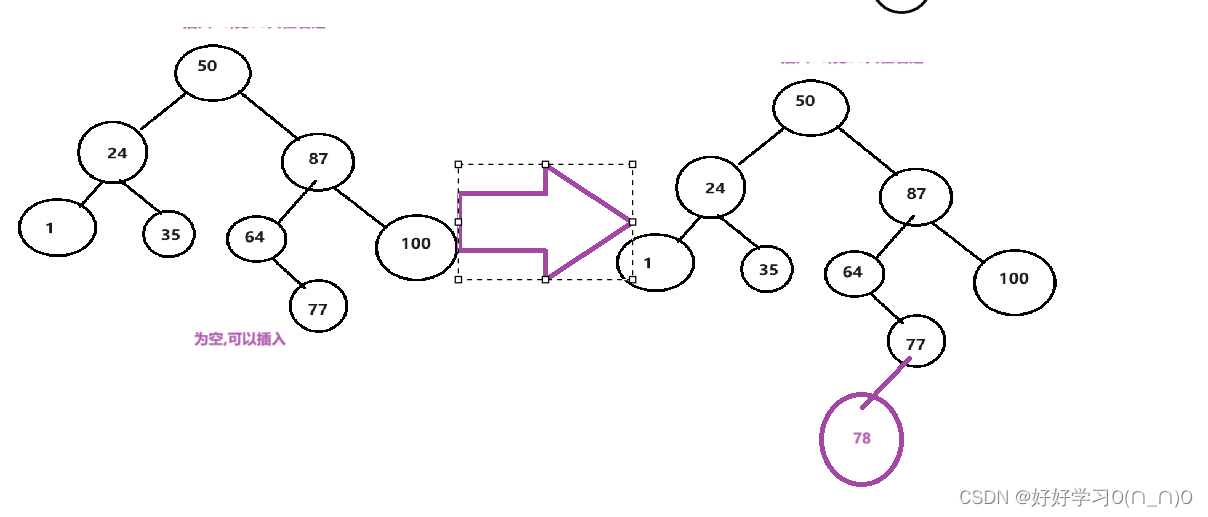
模拟实现

/*	template <class T>
	//二叉搜索的节点
	struct TreeNode {
		typedef TreeNode<T> Node;
		Node* _left;
		Node* _right;
		T  _val;
		//构造函数
		TreeNode(T val = T())
			:_left(nullptr),
			_right(nullptr),
			_val(val)
		{}
	};
*/

bool insert(T val) {
	if (_root == nullptr)
	{
		_root = new Node(val);
	}
	Node* child = _root;
	Node* parent = _root;
	while (child != nullptr) {
		parent = child;
		if (val < child->_val)	//val比根节点小,往左走
		{
			child = child->_left;
		}
		else if (val > child->_val)	//val比根节点大,往右走
		{
			child = child->_right;
		}
		else {
			return false;	//val与根节点相等,二叉搜索树中不许存在相同元素,所以不可插入,返回假
		}
	}
	if (parent->_val < val)	
		parent->_right = new Node(val);
	else if (parent->_val > val)	
		parent->_left = new Node(val);
	return true;	//插入成功
}

查找

查找与插入很类似,大于的话去右边找,小于的话去左边找,找到了返回节点,没找到返回nullptr

以找64为例

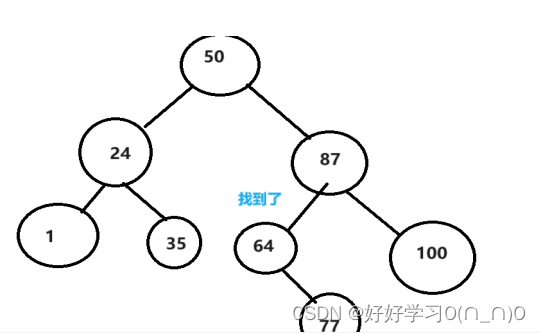
模拟实现

/*	template <class T>
	//二叉搜索的节点
	struct TreeNode {
		typedef TreeNode<T> Node;
		Node* _left;
		Node* _right;
		T  _val;
		//构造函数
		TreeNode(T val = T())
			:_left(nullptr),
			_right(nullptr),
			_val(val)
		{}
	};
*/

Node* find(T val) {
	Node* tmp = _root;
	while (tmp != nullptr) {
		if (val == tmp->_val)
			return tmp;	//找到啦
		else if (val > tmp->val) {
			tmp = tmp->_right;		//val大于该节点的值,去右子树找
		}
		else {
			tmp = tmp->_left;		//val小于该节点的值,去左子树找
		}
	}
	return nullptr;		//树里没有val,不存在该节点
}

删除

这边我们重画一个比较大一些的搜索二叉树以便于举例,数据很简单,1到16

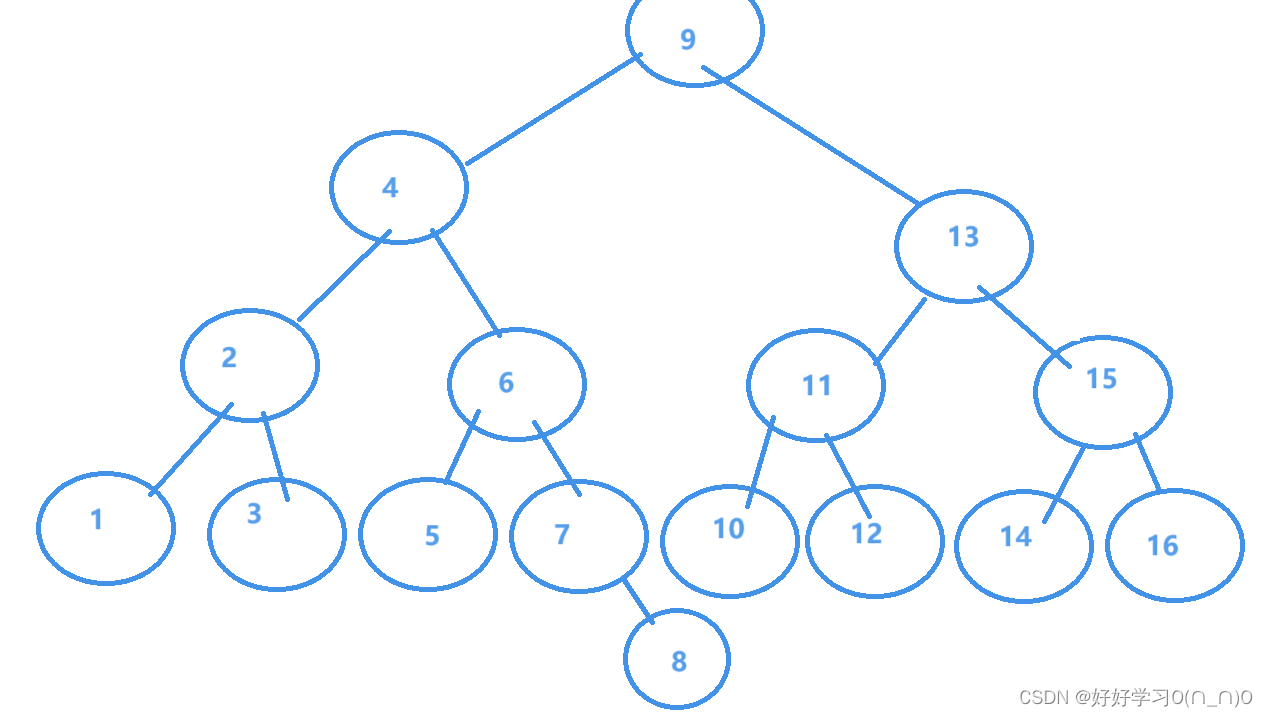
首先,当删去8时,其余的所有节点都仍旧符合搜索二叉树的定义,删去其他叶子节点有相同的效果,同理,在删去2节点时,理论上来说仅有2的子树受到影响,搜索树的其他部分仍旧符合定义.

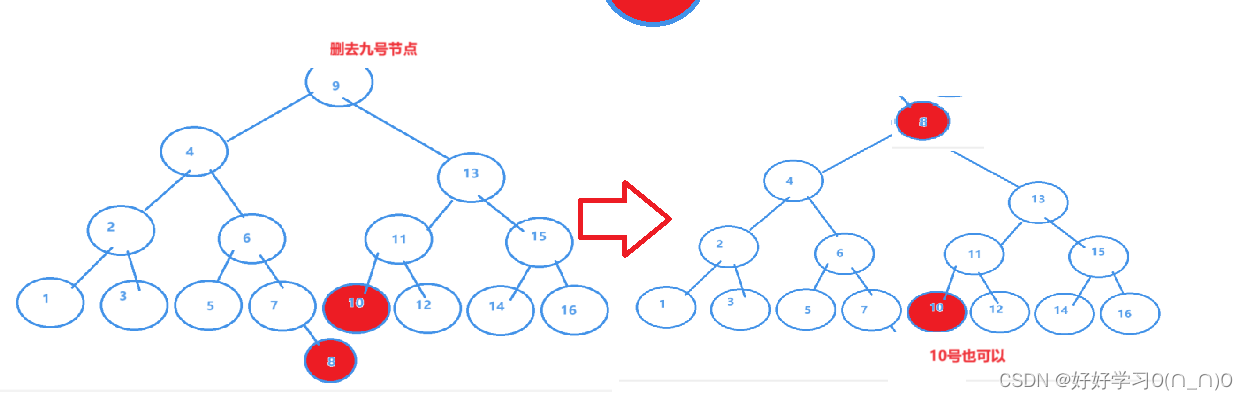
再以删去九号节点为例,由于二叉树的定义,删去九号节点后新节点的值必须满足除自身外,左子树都小于其,右子树都大于其.

由上图为例,对二叉树进行分析可得:除8外的左树<8<9<10<除10外的右树,也就是说:

左子树的右边的右边的右边的......的叶节点和右子树左边的左边的.......的叶节点最适合做根节点

特殊情况1:左子树没有右节点

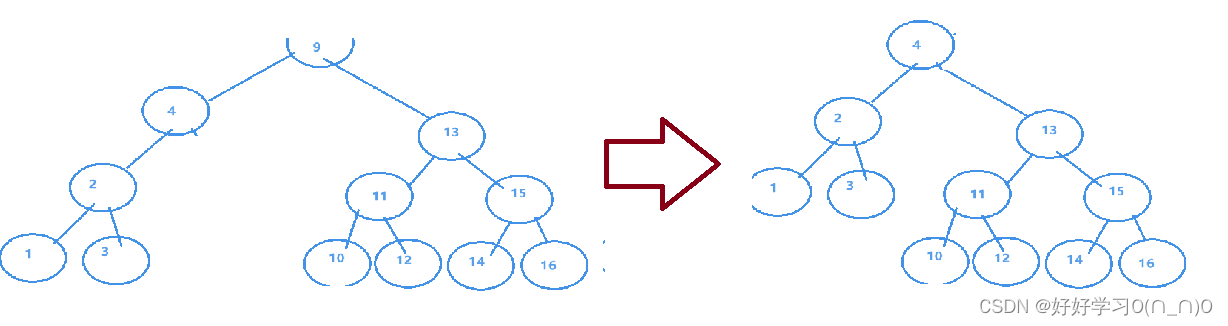
使用左子树自身的根节点即可.

特殊情况2:没有左子树&&只有一个孩子节点

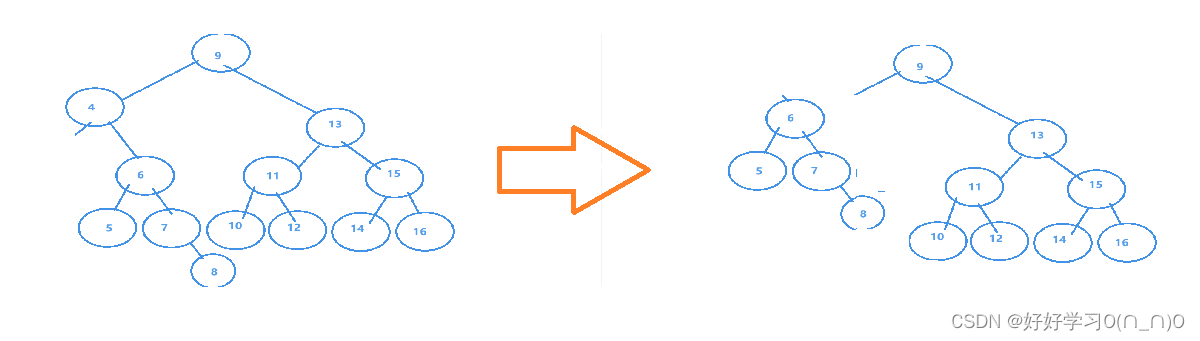
上图为删除节点4的示意图,可以看出,4号节点没有左子树,此时4号节点仅有一个子节点,直接让子节点代替自己即可


模拟实现

		bool earse(const T& val) {
			Node* parent = _root;
			Node* child = _root;
			while (child!= nullptr) {
				if (val > child->_val)
				{
					parent = child;
					child = child->_right;
				}
				else if (val < child->_val){
					parent = child;
					child = child->_left;
				}
				else   //相等
				{
					if (child->_left == nullptr)
					{
						if (child == _root)
							_root = child->_right;
						else {
							if (parent->_left == child)	parent->_left = child->_right;
							else if (parent->_right == child)	parent->_right = child->_right;
						}
						delete child;
					}
					else if (child->_right == nullptr) {
						if (child == _root)
							_root = child->_left;
						else {
							if (parent->_left == child)	parent->_left = child->_left;
							else if (parent->_right == child)	parent->_right = child->_left;
						}
						delete child;
					}
					else {
						Node* tmp = child->_left;
						Node* pp = tmp;

						while (tmp->_right) {
							pp = tmp;
							tmp = tmp->_right;
						}
						child->_val = tmp->_val;

						if (pp != tmp)
							pp->_right = tmp->_left;
						delete tmp;
					}
					return true;
				}
			}
			return false;
		}

高度(不重要)

	public:
		size_t height() {
			return _height(_root);
		}
	private:
		size_t _height(Node* root) {
			if (root == nullptr)
				return 0;
			else
				return _height(root->_left) + _height(root->_right) + 1;
		}

节点个数(不重要)

	public:
		size_t size() {
			return _size(_root);
		}
	private:
		size_t _size(Node* root) {
			if (root == nullptr)
				return 0;
			return _size(root->_left) + _size(root->_right) + 1;
		}

打印(不重要)

void print() {
	std::queue<Node*> q1,q2;
	q1.push(_root);
	while (!q1.empty() || !q2.empty()) {
		while (!q1.empty()) {
			if (q1.front() == nullptr)
				std::cout << '#' << ' ';
			else {
				q2.push(q1.front()->_left);
				q2.push(q1.front()->_right);
				std::cout << q1.front()->_val << ' ';
			}
			q1.pop();
		}
		std::swap(q1,q2);
		std::cout << std::endl;
	}

}

搜索二叉树模拟实现

#include <queue>
#include <iostream>
namespace SearchTree {
	template <class T>
	//二叉搜索的节点
	struct TreeNode {
		typedef TreeNode<T> Node;
		Node* _left;
		Node* _right;
		T  _val;
		//构造函数
		TreeNode(T val = T())
			:_left(nullptr),
			_right(nullptr),
			_val(val)
		{}
	};
	template <class T>
	class SearchTree {
		typedef TreeNode<T> Node;
		Node* _root;	//根节点
	public:
		SearchTree():_root(nullptr){}		//构造函数
		bool insert(T val) {
			if (_root == nullptr)
			{
				_root = new Node(val);
			}
			Node* child = _root;
			Node* parent = _root;
			while (child != nullptr) {
				parent = child;
				if (val < child->_val)	//val比根节点小,往左走
				{
					child = child->_left;
				}
				else if (val > child->_val)	//val比根节点大,往右走
				{
					child = child->_right;
				}
				else {
					return false;	//val与根节点相等,二叉搜索树中不许存在相同元素,所以不可插入,返回假
				}
			}
			if (parent->_val < val)	
				parent->_right = new Node(val);
			else if (parent->_val > val)	
				parent->_left = new Node(val);
			return true;	//插入成功
		}
		bool earse(const T& val) {
			Node* parent = _root;
			Node* child = _root;
			while (child!= nullptr) {
				if (val > child->_val)
				{
					parent = child;
					child = child->_right;
				}
				else if (val < child->_val){
					parent = child;
					child = child->_left;
				}
				else   //相等
				{
					if (child->_left == nullptr)
					{
						if (child == _root)
							_root = child->_right;
						else {
							if (parent->_left == child)	parent->_left = child->_right;
							else if (parent->_right == child)	parent->_right = child->_right;
						}
						delete child;
					}
					else if (child->_right == nullptr) {
						if (child == _root)
							_root = child->_left;
						else {
							if (parent->_left == child)	parent->_left = child->_left;
							else if (parent->_right == child)	parent->_right = child->_left;
						}
						delete child;
					}
					else {
						Node* tmp = child->_left;
						Node* pp = tmp;

						while (tmp->_right) {
							pp = tmp;
							tmp = tmp->_right;
						}
						child->_val = tmp->_val;

						if (pp != tmp)
							pp->_right = tmp->_left;
						delete tmp;
					}
					return true;
				}
			}
			return false;
		}
		Node* find(T val) {
			Node* tmp = _root;
			while (tmp != nullptr) {
				if (val == tmp->_val)
					return tmp;	//找到啦
				else if (val > tmp->val) {
					tmp = tmp->_right;		//val大于该节点的值,去右子树找
				}
				else {
					tmp = tmp->_left;		//val小于该节点的值,去左子树找
				}
			}
			return nullptr;		//树里没有val,不存在该节点
		}
		void print() {
			std::queue<Node*> q1,q2;
			q1.push(_root);
			while (!q1.empty() || !q2.empty()) {
				while (!q1.empty()) {
					if (q1.front() == nullptr)
						std::cout << '#' << ' ';
					else {
						q2.push(q1.front()->_left);
						q2.push(q1.front()->_right);
						std::cout << q1.front()->_val << ' ';
					}
					q1.pop();
				}
				std::swap(q1,q2);
				std::cout << std::endl;
			}

		}
		size_t size() {
			return _size(_root);
		}
		size_t height() {
			return _height(_root);
		}
	private:
		size_t _size(Node* root) {
			if (root == nullptr)
				return 0;
			return _size(root->_left) + _size(root->_right) + 1;
		}
		size_t _height(Node* root) {
			if (root == nullptr)
				return 0;
			else
				return std::max(_height(root->_left) , _height(root->_right)) + 1;
		}
	};
}

对搜索二叉树的分析及AVL树红黑树的优势

参考我在前文查找处的分析可得，查找的时间复杂度与树的高度，空间复杂度恒为o(1)，当插入从a到b的值是，优先输入[a,b]中间的值，后输入接近a,b的极端值，此时树较为平衡，查找的时间复杂度接近o(logn)，而当数据有序的进行插入时，树相当于一个链表，时间复杂度较高，为（o(n)）

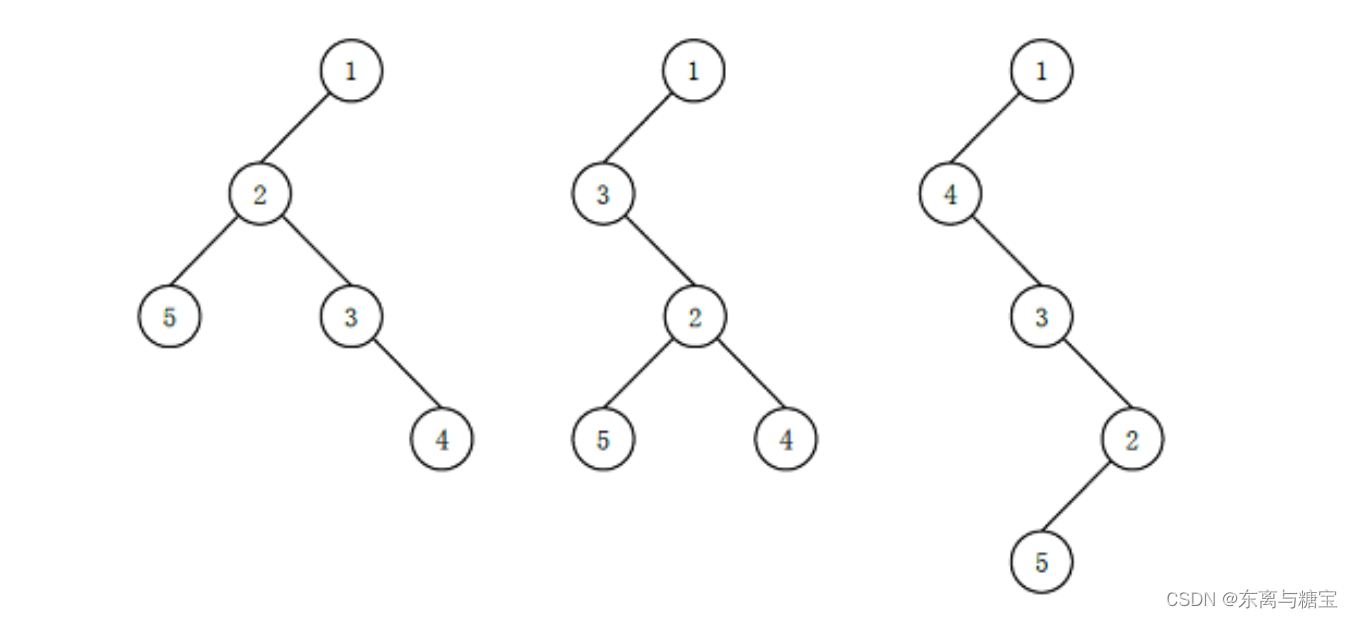
举个例子，当把数据[1,2,3,4,5,6,7]插入二叉树时

以[4,2,1,3,6,5,7]插入时，如果我们要查找7，需要进行三次判断即可，

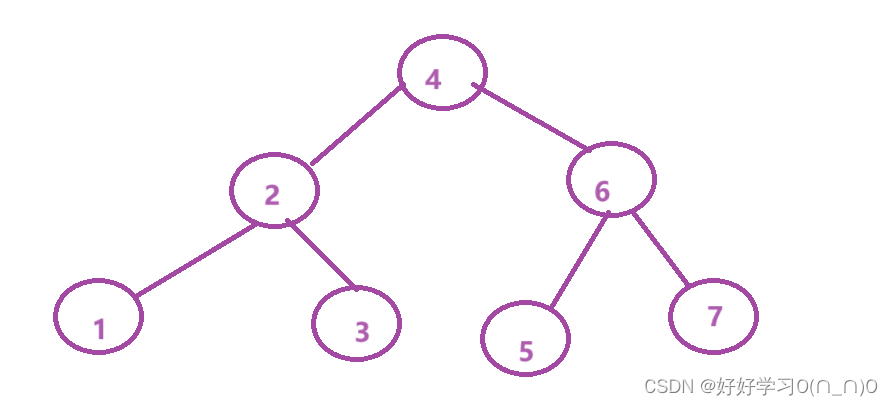
以[1,2,3,4,5,6,7]插入时，如果我们要查找7，需要进行七次判断！！！！时间复杂度为o(n)，再加上额外的空间开销，还不如直接在原数组中查找

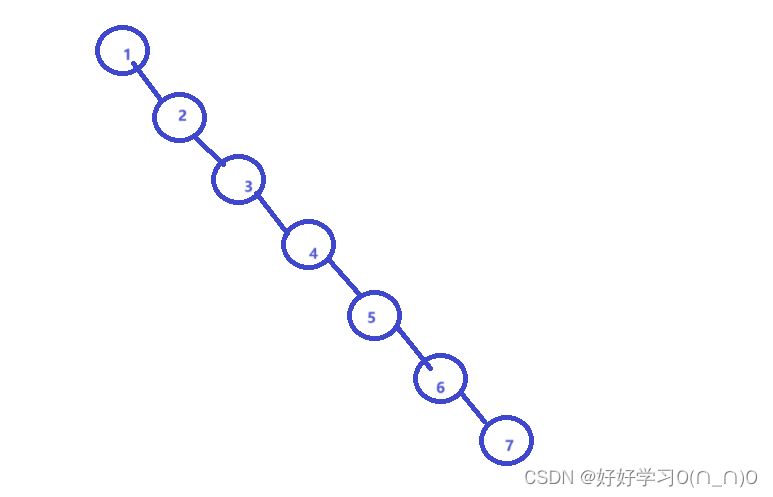
如果有一种改进的插入方式可以在插入时，依据原树的高度差进行动态的重构树结构，便可大大加快查找速度

附：AVL树模拟实现（供参考）

#include <queue>
#include <iostream>
#include <assert.h>
namespace AVL {

	template<class T>
	struct AVLTreeNode
	{
		AVLTreeNode(const T& data = T())
			: _pLeft(nullptr)
			, _pRight(nullptr)
			, _pParent(nullptr)
			, _data(data)
			, _bf(0)
		{}

		AVLTreeNode<T>* _pLeft;
		AVLTreeNode<T>* _pRight;
		AVLTreeNode<T>* _pParent;
		T _data;
		int _bf;   // 节点的平衡因子
	};


	// AVL: 二叉搜索树 + 平衡因子的限制
	template<class T>
	class AVLTree
	{
		typedef AVLTreeNode<T> Node;
	public:
		AVLTree()
			: _pRoot(nullptr)
		{}
		void print() {
			std::queue<Node*>q1;
			std::queue<Node*>q2;
			q1.push(_pRoot);
			while (!q1.empty() || !q2.empty()) {
				while (!q1.empty())
				{
					if (q1.front() != nullptr) {
						std::cout << q1.front()->_data << ' ';
						q2.push(q1.front()->_pLeft);
						q2.push(q1.front()->_pRight);
					}
					else
						std::cout << '#' << ' ';
					q1.pop();
				}
				swap(q1, q2);
				std::cout << std::endl;
			}
		}
		// 在AVL树中插入值为data的节点
		bool Insert(const T& data) {
			Node* node = new Node(data);
			if (_pRoot == nullptr) {
				_pRoot = node;
				return true;
			}
			Node* parent = _pRoot,*child = _pRoot;
			while (child) {
				parent = child;
				if (child->_data > data)	child = child->_pLeft;
				else if (child->_data < data)	child = child->_pRight;
				else return false;
			}
			if (parent->_data < data)
			{
				parent->_pRight = node;
			}
			else
			{
				parent->_pLeft = node;
			}
			node->_pParent = parent;
			while (parent) {
				if (node == parent->_pLeft)
					parent->_bf--;
				else
					parent->_bf++;
				if (parent->_bf == 0)
					break;
				else if (parent->_bf == 1 || parent->_bf == -1)
					node = parent, parent = parent->_pParent;
				else {		//出问题了
					if (parent->_bf == -2 && node->_bf == -1) {
						RotateR(node);
					}
					else if (parent->_bf == -2 && node->_bf == 1)
					{
						RotateLR(node);
					}
					else if (parent->_bf == 2 && node->_bf == 1) {
						RotateL(parent);
					}
					else if (parent->_bf == -2 && node->_bf == -1) {
						RotateRL(node);
					}
					else {
						//   树损坏
					}
				}
			}
			return true;
		}

		// AVL树的验证
		bool IsAVLTree()
		{
			return _IsAVLTree(_pRoot);
		}

	private:
		// 根据AVL树的概念验证pRoot是否为有效的AVL树
		bool _IsAVLTree(Node* pRoot) {
			std::queue<Node*> q;
			q.push(pRoot);
			while (!q.empty()) {
				if (q.front() == nullptr)
				{
					q.pop();
					continue;
				}
				if (q.front()->_bf >= 2 || q.front()->_bf <= -2)
				{
					return false;
				}
				else {
					q.push(q.front()->_pLeft);
					q.push(q.front()->_pRight);
					q.pop();
				}
			}
			return true;
		}
		size_t _Height(Node* pRoot) {
			size_t h = 0;
			std::queue<Node*> q1;
			std::queue<Node*> q2;
			q2.push(pRoot);
			while (!q1.empty()&&!q2.empty()) {
				while (!q1.empty())
				{
					if (q1.front() != nullptr)
					{
						q2.push(q1.front()->_pLeft);
						q2.push(q1.front()->_pRight);
					}
					q1.pop();
				}
				std::swap(q1, q2);
				h++;
			}
			q1.empty();
			q2.empty();
			return h - 1;
		}
		// 左单旋
		void RotateL(Node* pParent) {
			//新的头节点
			Node* new_Parent = pParent->_pRight;
			//旧头结点的父节点
			Node* grand = pParent->_pParent;
			//修改pParent的父节点
			if (grand != nullptr)
			{
				if (grand->_pLeft == pParent)
					grand->_pLeft = new_Parent;
				else
					grand->_pRight = new_Parent;
			}
			else {
				_pRoot = new_Parent;
			}
			// 修改pParent节点
			pParent->_pParent = new_Parent;
			pParent->_pRight = new_Parent->_pLeft;

			//修改new_Parent节点
			if(new_Parent->_pLeft!=nullptr)
				new_Parent->_pLeft->_pParent = pParent;
			new_Parent->_pLeft = pParent;
			new_Parent->_pParent = grand;
			pParent->_pParent = new_Parent;

			pParent->_bf = new_Parent->_bf = 0;
		}
		// 右单旋
		void RotateR(Node* pParent) {
			//新的头节点
			Node* new_Parent = pParent->_pLeft;
			//旧头结点的父节点
			Node* grand = pParent->_pParent;
			//修改pParent的父节点
			if (grand != nullptr)
			{
				if (grand->_pLeft == pParent)
					grand->_pLeft = new_Parent;
				else
					grand->_pRight = new_Parent;
			}
			else {
				_pRoot = new_Parent;
			}
			// 修改pParent节点
			pParent->_pParent = new_Parent;
			pParent->_pLeft = new_Parent->_pRight;

			//修改new_Parent节点
			if(new_Parent->_pRight!=nullptr)
				new_Parent->_pRight->_pParent = pParent;
			new_Parent->_pRight = pParent;
			new_Parent->_pParent = grand;
			pParent->_pParent = new_Parent;

			pParent->_bf = new_Parent->_bf = 0;
		}
		// 右左双旋
		void RotateRL(Node* pParent) {
			RotateR(pParent);
			RotateL(pParent->_pParent->_pParent);
		}
		// 左右双旋
		void RotateLR(Node* pParent) {
			RotateL(pParent);
			RotateR(pParent->_pParent->_pParent);
		}
	protected:
		Node* _pRoot;

	};
}

结语

截止至结语，本文已有接近1万字，制作不易可以留个免费的赞吗

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1668744.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

kilimall非洲电商培训，基础版+进阶版+高阶版 从0-1个人可入驻的平台（12节）

kilimall非洲电商培训，基础版+进阶版+高阶版 从0-1个人可入驻的平台（12节）

亲爱的朋友们&#xff0c;你们知道吗&#xff1f;有一个神奇的电商平台——kilimall&#xff0c;它可以帮助你实现创业梦想&#xff0c;让你走上财富之路&#xff01; 首先&#xff0c;让我给大家介绍kilimall的基础版。基础版针对的是0经验的小白&#xff0c;提供了详细的教程…
阅读更多...
vscode打开esp-idf工程，找不到头文件，有波浪线

vscode打开esp-idf工程，找不到头文件，有波浪线

就像这样 多半是因为原始的工程不是用vscode的插件新建的&#xff0c;因此没有相关的路径。需要在工程文件夹下的.vscode文件夹中的c_cpp_properties.json文件中增加路径&#xff0c;可以参考插件自动新建的工程里面的写法 {"configurations": [{"name":…
阅读更多...
TeXlive TeXstudio安装指南

TeXlive TeXstudio安装指南

TeXlive & TeXstudio安装指南 记上次安装Visual Studio Code (Vscode)配置LaTeX后&#xff0c;由于Overleaf页数太多&#xff0c;项目超过了免费计划的编译时限&#xff08;这两天突然出现这个问题&#xff09;。加上毕设和PPT都是在Overleaf上编译&#xff0c;这两天突然…
阅读更多...
第十二届蓝桥杯省赛真题 Java A 组【原卷】

第十二届蓝桥杯省赛真题 Java A 组【原卷】

文章目录 发现宝藏【考生须知】试题 A: 相乘试题 B: 直线试题 C : \mathrm{C}: C: 货物摆放试题 D: 路径试题 E: 回路计数试题 F : \mathrm{F}: F: 最少砝码试题 G: 左孩子右兄弟试题 H : \mathrm{H}: H: 异或数列试题 I \mathbf{I} I 双向排序试题 J : \mathrm{J}: J: 分…
阅读更多...
electron进程间通信

electron进程间通信

Electron 应用程序的结构非常相似。 作为应用开发者&#xff0c;你将控制两种类型的进程&#xff1a;主进程 和 渲染器进程。 这类似于上文所述的 Chrome 的浏览器和渲染器进程。 主进程 每个 Electron 应用都有一个单一的主进程&#xff0c;作为应用程序的入口点。 主进程在 N…
阅读更多...
STM32快速入门（总线协议之I2C一主多从（软件实现 硬件实现））

STM32快速入门（总线协议之I2C一主多从（软件实现 硬件实现））

STM32快速入门&#xff08;总线协议之I2C一主多从&#xff08;软件实现 & 硬件实现&#xff09;&#xff09; 前言 支持一对多&#xff08;一主多从&#xff09;、多对多传输&#xff08;多主多从&#xff09;&#xff0c;只支持半双工&#xff0c;一般有两根数据线&…
阅读更多...
蓝桥之链表

蓝桥之链表

最近真的特别焦虑&#xff0c;体测、比赛和考试一个接一个&#xff0c;让人喘不过气来QAQ 甚至考试和比赛还有冲突&#xff0c;sad 最近因为看了牙&#xff0c;打了药的缘故&#xff0c;一直在吃素QAQ 本来今天还想写个知识点总结的&#xff0c;但是太晚了&#xff0c;现在已…
阅读更多...
吃透前端文件上传与文件相关操作

吃透前端文件上传与文件相关操作

最近在学文件上传的操作,所以想把学习到东西写成一文章 这片文章是我以小白视角 慢慢学习并熟悉前端文件相关操作的流程总结出来的 前端文件上传 我首先想到是 <input type"file">选择文件</input>如果我们想限制上传文件的格式,大小或进行裁剪分片上传…
阅读更多...
2022——蓝桥杯十三届2022国赛大学B组真题

2022——蓝桥杯十三届2022国赛大学B组真题

问题分析 看到这个问题的同学很容易想到用十层循环暴力计算&#xff0c;反正是道填空题&#xff0c;一直算总能算得出来的&#xff0c;还有些同学可能觉得十层循环太恐怖了&#xff0c;写成回溯更简洁一点。像下面这样 #include <bits/stdc.h> using namespace std; in…
阅读更多...
树莓派4B-搭建一个本地车牌识别服务器

树莓派4B-搭建一个本地车牌识别服务器

实现目标&#xff1a; 一、设备自启后能够获得服务的ip与端口号&#xff0c;用于计算机连接设备&#xff1b; 二、计算机可以通过服务ip与端口访问设备服务&#xff1b; 三、上传需要处理的数据&#xff0c;返回结果反馈给用户&#xff1b; 四、上传到服务器的数据不会导致设备…
阅读更多...
Study--Oracle-02-单实例部署Oracle19C

Study--Oracle-02-单实例部署Oracle19C

一、CentOS 7 环境准备 1、软件准备 操作系统&#xff1a;CentOS 7 数据库版本: Oracle19C 2、操作系统环境配置 关闭selinux &#xff0c;编辑 /etc/selinux/config文件&#xff0c;设置SELINUX enforcing 为SELINUXdisabled [rootoracle ~]# grep SELINUX /etc/seli…
阅读更多...
手游掘金最新玩法，单条视频变现1w+，一部手机即可操作，保姆级教程

手游掘金最新玩法，单条视频变现1w+，一部手机即可操作，保姆级教程

如果你也想通过手机赚钱&#xff0c;在这里有一个非常好的项目&#xff0c;它可以让你轻松赚到额外的收入。 这个手游掘金最新玩法&#xff0c;是一个非常受欢迎的项目&#xff0c;它可以让你通过制作单条视频来获得高额收益。不同于传统的游戏赚钱方式&#xff0c;这个方法不…
阅读更多...
HTML表单创建学习

HTML表单创建学习

文章目录 1、创建HTML框架2.body标签CSS3.表单创建3.1、添加fieldset与label标签3.2、为label标签添加css样式3.3、添加input标签3.4、添加提交按钮3.5、在input标签中添加required3.6、添加minlength属性3.7、pattern属性3.8、设置表单单选按钮无法同时选中3.9、添加链接3.10、…
阅读更多...
SpringSecurity的核心原理使用总结

SpringSecurity的核心原理使用总结

1. SpringSecurity的核心原理 对于最原始Servlet请求处理的层次结构 客户端->过滤器链->Servlet 对于在SpringMVC中处理请求的层次结构 如何让Filter与Spring建立连接呢? 因此它增加了一个DelegatingFilterProxy 它是SpringMVC提供的的Filter,它内部代理了一个原生的F…
阅读更多...
HC-06 蓝牙串口从机 AT 命令详解

HC-06 蓝牙串口从机 AT 命令详解

HC-06 蓝牙串口从机 AT 命令详解 要使用 AT 命令&#xff0c;首先要知道 HC-06 的波特率&#xff0c;然后要进入 AT 命令模式。 使用串口一定要知道三要素&#xff0c;一是波特率&#xff0c;二是串口号&#xff0c;三是数据格式, HC-06只支持一种数据格式: 数据位8 位&#…
阅读更多...
测试平台开发：Django开发实战之注册界面实现(上)

测试平台开发：Django开发实战之注册界面实现(上)

实现注册功能&#xff0c;大概包括以下几个步骤 1、设计ui ##字段 通过看数据库里面的user表里面的字段&#xff0c;可以大概知道需要几个字段&#xff1a; emailusernamepasswordpassword_confirm 生成简单的ui界面&#xff0c;复制这个html代码 然后在项目路径下面创建一…
阅读更多...
transformer与beter

transformer与beter

transformer与beter 解码和编码器含义tokizer标记器和one-hot独热编码编码解码--语义较好的维度空间矩阵相乘--空间变换编码理解如何构造降维的嵌入矩阵--实现到达潜空间上面是基础&#xff0c;下面是transformer正文自注意力机制注意力分数--上下文修正系数为什么需要KQ两个矩…
阅读更多...
KAN 笔记

KAN 笔记

1 Title KAN: Kolmogorov–Arnold Networks&#xff08;Ziming Liu, Yixuan Wang, Sachin Vaidya, Fabian Ruehle, James Halverson, Marin Soljačić, Thomas Y. Hou, Max Tegmark&#xff09;【2024】 2 Conclusion Inspired by the Kolmogorov-Arnold representat…
阅读更多...
函数式接口-闭包与柯里化

函数式接口-闭包与柯里化

闭包 定义 示例 注意 这个外部变量 x 必须是effective final 你可以生命他是final&#xff0c;你不声明也会默认他是final的&#xff0c;并且具有final的特性&#xff0c;不可变一旦x可变&#xff0c;他就不是final&#xff0c;就无法形成闭包&#xff0c;也无法与函数对象一…
阅读更多...
《Python编程从入门到实践》day26

《Python编程从入门到实践》day26

# 昨日知识点回顾 添加Play按钮创建Button类绘制按钮开始游戏、游戏结束重制游戏影藏鼠标光标 # 今日知识点学习 14.2 提高等级 14.2.1 修改速度设置 # Settings.py# 加快游戏节奏的速度self.speedup_scale 1.1self.initialize_dynamic_settings()def initialize_dynamic_se…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023