制作不易,三连支持一下呗!!!
文章目录
- 前言
- 一、二叉树链式结构的实现
- 总结
前言
这篇博客我们将来了解普通二叉树的实现和应用,对大家之前分治和递归的理解有所挑战。
一、二叉树链式结构的实现
1.前置说明
在学习二叉树的基本操作前,需要先创建一棵二叉树,然后才能学习其相关的基本操作,由于我们现在对二叉树结构的掌握还不够深入,此处手动快速创建一棵二叉树,等二叉树结构了解差不多时,再研究二叉树真正的创建方法。
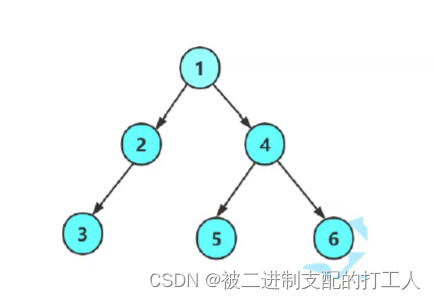
我们已这棵树的结构为例,手动创建一颗二叉树。
typedef int BTDataType;
typedef struct BinTreeNode
{
struct BinTreeNode* left;
struct BinTreeNode* right;
BTDataType val;
}BTNode;
BTNode* BuyBTNode(BTDataType x)
{
BTNode* newnode = (BTNode*)malloc(sizeof(BTNode));
if (newnode == NULL)
{
perror("buynode:");
return;
}
newnode->left = newnode->right = NULL;
newnode->val = x;
return newnode;
}
BTNode* CreatTree()
{
BTNode* n1 = BuyBTNode(1);
BTNode* n2 = BuyBTNode(2);
BTNode* n3 = BuyBTNode(3);
BTNode* n4 = BuyBTNode(4);
BTNode* n5 = BuyBTNode(5);
BTNode* n6 = BuyBTNode(6);
n1->left = n2;
n1->right = n4;
n2->left = n3;
n4->left = n5;
n4->right = n6;
return n1;
}2.二叉树的遍历
①前序遍历
根左右。前序遍历首先访问根结点然后遍历左子树,最后遍历右子树。在遍历左、右子树时,仍然先访问根节点,然后遍历左子树,最后遍历右子树。
若二叉树为空则结束返回,否则:
(1)访问根结点。
(2)前序遍历左子树。
(3)前序遍历右子树 。
需要注意的是:遍历左右子树时仍然采用前序遍历方法。
根据前序遍历的概念可以看出,前序遍历是递归展开的。我们代码实现时就应该按照分治的思想来书写。
//前序遍历
void PreOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
printf("%d ", root->val);
PreOrder(root->left);
PreOrder(root->right);
}在用分治思想解决问题时,我们要抓住这两个重点:
1.想清楚子问题是什么
2..想清楚什么时候是最小子问题。
例如上面二叉树的前序遍历,子问题就是要想遍历这棵树要将它分为根,左子树,右子树。
左子树又分为根,左子树,右子树……依次类推。最小子问题就是当这棵树为空树也就是NULL时,我们逐层返回。
②中序遍历
左根右。中序遍历首先遍历左子树,然后访问根结点,最后遍历右子树。
与前序遍历类似,代码实现如下:
//中序遍历
void InOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
PreOrder(root->left);
printf("%d ", root->val);
PreOrder(root->right);
}③后序遍历
左右根。后序遍历首先遍历左子树,然后遍历右子树,最后访问根结点,在遍历左、右子树时,仍然先遍历左子树,然后遍历右子树,最后遍历根结点。即:
若二叉树为空则结束返回,
否则:
(1)后序遍历左子树
(2)后序遍历右子树
(3)访问根结点
//后序遍历
void PostOrder(BTNode* root)
{
if (root == NULL)
{
printf("N ");
return;
}
PreOrder(root->left);
PreOrder(root->right);
printf("%d ", root->val);
}④层序遍历
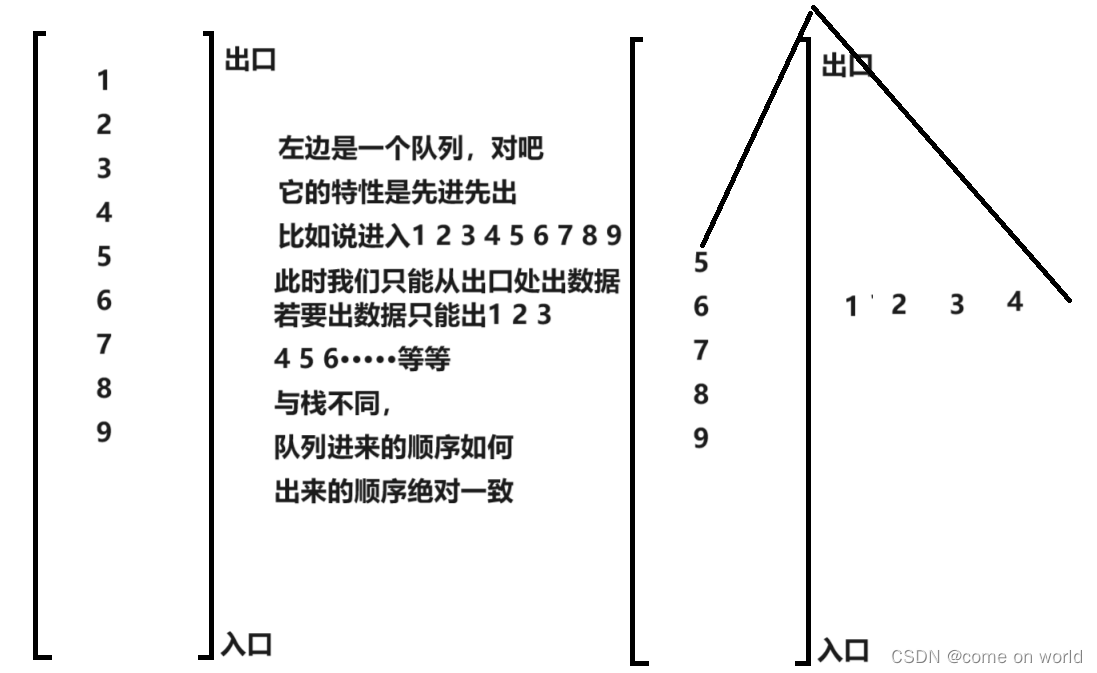
层序遍历就是一层一层按顺序遍历树,方法就是借助队列的性质,出队列一个就带两个子节点就队列的方法来遍历,直到队列为空,如果出队列的节点为空就不带节点进队列了!!!
void TreeLevelOrder(BTNode* root)
{
Queue q;
QueueInit(&q);
if (root)
QueuePush(&q, root);
while (!QueueEmpty(&q))
{
BTNode* front = QueueFront(&q);
QueuePop(&q);
if (front)
{
printf("%d ", front->val);
// 带入下一层
QueuePush(&q, front->left);
QueuePush(&q, front->right);
}
else
{
printf("N ");
}
}
printf("\n");
QueueDestroy(&q);
}3.求二叉树的节点数
这里我们要写一个求给定二叉树有多少节点的接口
我们还是采用分治的思想,要求一颗二叉树有多少节点还是将它分为左子树和右子树,先求出左右子树有多少节点,最后再加上根节点这一个就可以了。最小子问题还是遇到空树就返回0个节点。
int TreeSize(BTNode* root)
{
return root == NULL ? 0
: TreeSize(root->left) + TreeSize(root->right) + 1;
}4.求二叉树的深度
我们还是采用分治的思想,要求一颗二叉树的深度还是将它分为左子树和右子树,先求出左右子树的深度中的最大值,再加上根节点的1。最小子问题还是遇到空树就返回0。
int TreeHeight(BTNode* root)
{
if (root == NULL)
{
return 0;
}
int leftdepth = TreeHeight(root->left);
int rightdepth = TreeHeight(root->right);
return (leftdepth > rightdepth ? leftdepth : rightdepth) + 1;
}这里有一个注意点:
可能有些同学会试图将代码简化,不创建leftdepth和rightdepth两个变量,直接返回。

单从结果上来看,这样写是没有什么问题的。问题出在这样写会使时间复杂度暴增。
之前时间复杂度是O(N),但现在时间复杂度甚至接近2^N。
在leetcode上有一道求二叉树深度题目,如果用改动之后的代码提交上无法通过的,因为效率太低了。
. - 力扣(LeetCode)
5.求第K层节点个数
分治思想:要求第K层节点个数可将问题拆分为求左子树的第K-1层的节点个数和右子树的第K-1层节点个数之后,依此类推。
最小子问题①非空且K==1时就返回1,
②如果根已经为空就返回0。
int TreeKLevel(BTNode* root, int k)
{
assert(k > 0);
if (NULL == root)
return 0;
if (k == 1)
return 1;
//如果不为空且k不等于1,就说明第k层在子树中,转换为子问题求解
return TreeKLevel(root->left, k - 1) + TreeKLevel(root->right, k - 1);
}6.查找值为x的节点的位置
分治思想:子问题是在左子树找和在右子树找
最小子问题是:如果根为空就返回空,如果根不为空且val==x就返回root
BTNode* TreeFind(BTNode* root, int x)
{
if (root == NULL)
return NULL;
if (root->val == x)
return root;
BTNode* ret1 = TreeFind(root->left, x);
if (ret1)
return ret1;
return TreeFind(root->right, x);
}7. 二叉树的创建和销毁
1.创建
二叉树的创建要依靠前序遍历的结果或中序遍历的结果或后序遍历的结果来构建,后面我们有相关题目,这里不多赘述。
2.销毁
void TreeDestroy(BTNode* root)
{
if (root == NULL)
return;
TreeDestroy(root->left);
TreeDestroy(root->right);
free(root);
root = NULL;
}总结
我们详细了解了二叉树的存储结构,并初步领会了分治思想