1.题目
11. 盛最多水的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
示例 1:
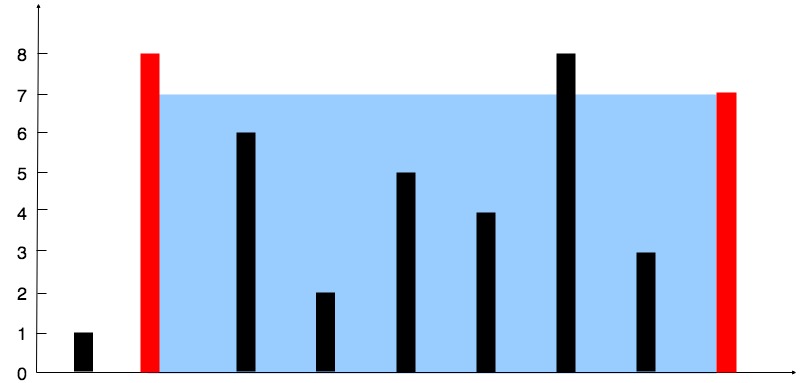
输入:[1,8,6,2,5,4,8,3,7] 输出:49 解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
示例 2:
输入:height = [1,1] 输出:1
提示:
n == height.length2 <= n <= 1050 <= height[i] <= 104
2.解法⼀(暴⼒求解)(会超时):
时间复杂度:
算法思路:
枚举出能构成的所有容器,找出其中容积最⼤的值。
◦ 容器容积的计算⽅式:
设两指针i, j 分别指向⽔槽板的最左端以及最右端,此时容器的宽度为j - i 。由于
容器的⾼度由两板中的短板决定,因此可得容积公式:
v = (j - i) * min(height[i], height[j])

class Solution {
public:
int maxArea(vector<int>& height) {
int n = height.size();
int ret = 0;
// 两层 for 枚举出所有可能出现的情况
for (int i = 0; i < n; i++) {
for (int j = i + 1; j < n; j++) {
// 计算容积,找出最⼤的那⼀个
ret = max(ret, min(height[i], height[j]) * (j - i));
}
}
return ret;
}
};
3.解法⼆(对撞指针):
算法思路:
设两个指针 left , right 分别指向容器的左右两个端点,此时容器的容积:
v = (right - left) * min( height[right], height[left])
容器的左边界为height[left] ,右边界为height[right] 。
为了⽅便叙述,我们假设「左边边界」⼩于「右边边界」。
如果此时我们固定⼀个边界,改变另⼀个边界,⽔的容积会有如下变化形式:◦ 由于左边界较⼩,决定了⽔的⾼度。如果改变左边界,新的⽔⾯⾼度不确定,但是⼀定不会超过右边的柱⼦⾼度,因此容器的容积可能会增⼤。
◦ 如果改变右边界,⽆论右边界移动到哪⾥,新的⽔⾯的⾼度⼀定不会超过左边界,也就是不会超过现在的⽔⾯⾼度,但是由于容器的宽度减⼩,因此容器的容积⼀定会变⼩的。
由此可⻅,左边界和其余边界的组合情况都可以舍去。所以我们可以 left++ 跳过这个边界,继续去判断下⼀个左右边界。
当我们不断重复上述过程,每次都可以舍去⼤量不必要的枚举过程,直到 left 与right 相
遇。期间产⽣的所有的容积⾥⾯的最⼤值,就是最终答案。



![]() 直到 left 与right 相遇
直到 left 与right 相遇

4.代码实现
1.C语言
int min(int a, int b) {
if (a < b) {
return a;
} else {
return b;
}
}
int max(int num1, int num2) {
return (num1 > num2 ) ? num1 : num2;
}
int maxArea(int* height, int heightSize)
{
int left = 0, right = heightSize- 1, ret = 0;
while (left < right) {
int v = min(height[left], height[right]) * (right - left);
ret = max(ret, v);
// 移动指针
if (height[left] < height[right])
left++;
else
right--;
}
return ret;
}
2.C++
class Solution {
public:
int maxArea(vector<int>& height) {
int left = 0, right = height.size() - 1, ret = 0;
while (left < right) {
int v = min(height[left], height[right]) * (right - left);
ret = max(ret, v);
// 移动指针
if (height[left] < height[right])
left++;
else
right--;
}
return ret;
}
};