众所周知,
语言模型调参!
预训练语言模型调参!!
预训练大语言模型调参!!!
简直就是一个指数级递增令人炸毛的事情,小编也常常在做梦,要是只训练几步就知道现在的超参数或者数据配比能不能行,那该有多好。
但现在,有一篇工作似乎正在令小编的梦想成为现实,那就是清华大学提出的Temporal Scaling Law。根据他们提出的这条规则,便可以通过当前训练步来准确预测未来训练步损失(loss)的下降情况,从而可以极大程度上提高各位炼丹师的效率。
此外,正所谓“重剑无锋,大巧不工”,这篇研究还发现在训练过程中并不需要针对token position添加权重,默认的预训练模式就足以达到非常好的效果。
GPT-3.5研究测试:
yeschat
GPT-4研究测试:
Hello, LLMs
Claude-3研究测试(全面吊打GPT-4):
AskManyAI
论文标题Temporal Scaling Law for Large Language Models
论文链接https://arxiv.org/pdf/2404.17785
Scaling Law
在介绍本文工作之前,先来回顾一下2020年由Kaplan等人首次提出的Scaling Law,即对于生成式Transformer模型,测试损失与模型大小、数据集大小和用于训练的计算量之间存在幂律关系(power-law relationship)。
此后,也陆续有研究在迁移学习(transfer-learning)和多模态预训练(multi-modal pre-training)验证了scaling law的存在。
Temporal Scaling Law
1. 从Scaling Law到Temporal Scaling Law
如前文所述,Scaling Law更侧重于建立测试损失与各个静态属性之间的关系,尽管Kaplan等人也提出测试损失与训练步之间遵从幂律,但这是建立在无限训练数据和训练步数前提下的,而这显然不符合我们的现实情况。
因此,本文在Scaling Law的基础上,进一步提出了考虑训练时间维度的Temporal Scaling Law,用以描述训练步与测试损失之间的关系,从而勾勒出大语言模型(LLMs)的预训练轨迹。
2. 实验设置
-
训练数据:本文选用了Pile数据集作为预训练数据,这是一个包括22个领域的单语言大规模数据集
-
测试数据:为度量测试损失,本文构造了两个测试数据,包括一个同样来自Pile的同分布数据集(IID-Val)和一个来自PG-19的异分布数据集(OOD-Val),都处理成1024 tokens的长度。测试损失取测试集中的所有序列损失的平均
-
模型选择:本文选用了468M和1.2B两种大小的生成式语言模型
-
训练方法:所有模型都需要经过400B tokens的训练,为捕捉时间维度训练进展,本文在训练阶段每隔1B个tokens创建一个checkpoint,并使用这些checkpoint进行测试损失评估
-
度量指标:为评估temporal scaling law的预测结果对真实测试损失的拟合情况,本文采用了可决指数(coefficient of determination,)和均方误差(mean-square error,),前者表示所提出模型可解释原始数据方差的比例,后者度量所提出模型的预测结果对真实值的误差
3. Temporal Scaling Law
语言模型的本质是经过训练的统计模型,即根据先前所有token对下一个token的概率分布进行预测建模。,其中。因此,对于一个连续的序列,我们通常会认为位于后面的token会比位于前面的token更好预测,因为它有更多的背景信息,即:
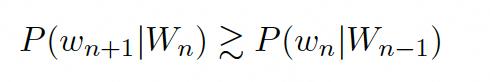
为验证这一假设,本文在IID-Val数据集上用468M和1.2B模型预训练400B tokens进行实验
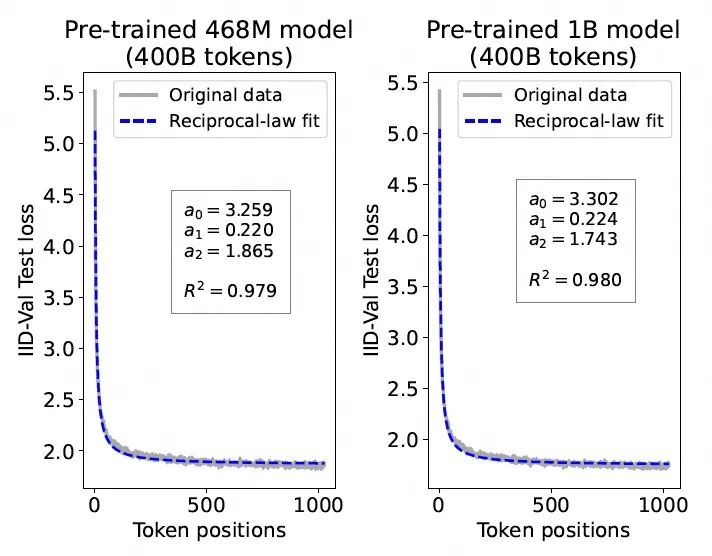
与假设一致,在两种大小的模型上都呈现出一致的规律,即输入序列中位置更靠前的token(背景信息更少)往往有更高的测试损失,而随着token位置越来越靠后逐渐收敛到一个固定的数值。通过以下倒数关系(reciprocal-law)的等式来拟合这种趋势,其中为token在输入序列中的位置
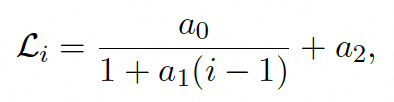
其中,,和为拟合参数。其中,表示序列第一个token和最后一个token之间的损失差,为基于序列长度的缩放因子,为收敛因子,表示随着上下文的延长,每个token上损失的收敛值。下图展示了在468M模型的整个预训练阶段,IID Val上,,和的拟合曲线。
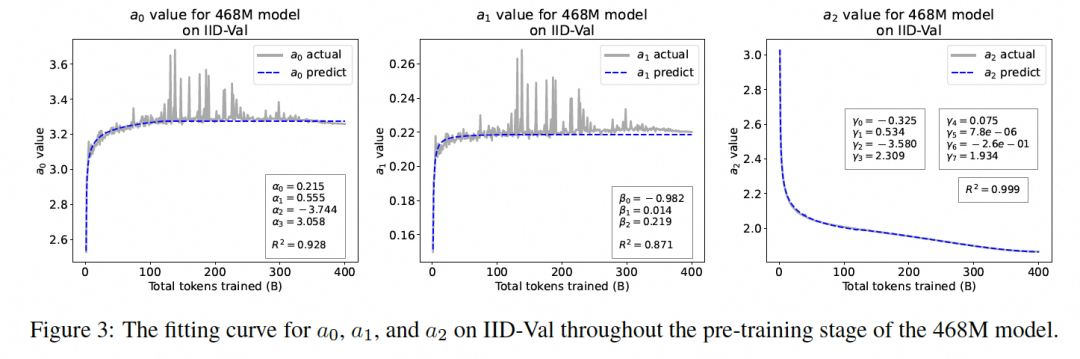
当时(表示总训练步数),和收敛。因此,对于,取, 。此外还发现与学习率衰减呈强相关关系。
最终,未来测试损失可通过平均所有token位置的损失以进行预测:
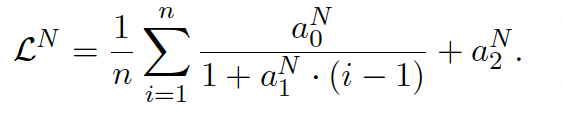
对比基于Kaplan等人幂律,倒数和对数关系的baseline,通过Temporal Scaling Law的未来损失预测具有显著优势:
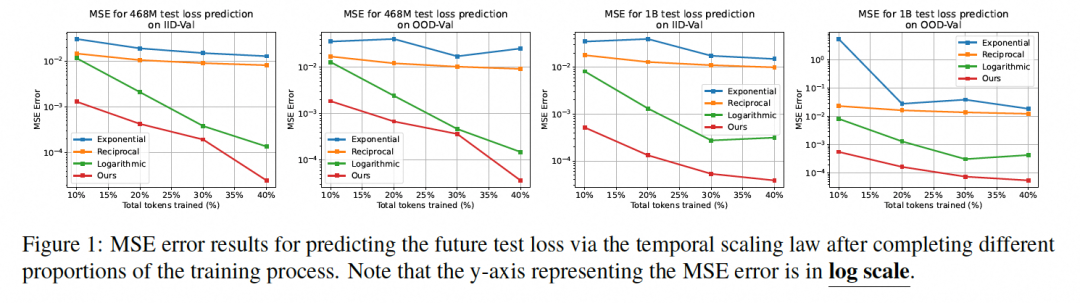
4. 不同token位置加权重?
前面的实验发现,位于输入序列头部的token往往更难预测,但随着训练更多的tokens以后,和逐渐趋于平稳,意味着LLMs开始对于不同位置的token平等学习。那么是否还需要对不同位置的token加不同权重以促进模型学习呢?
为验证这一点,本文将默认的预训练方法与3种简单的加权方法在8个公开评测数据上进行对比,分别是
-
头部抑制:头部10%的token计算损失时乘以0.5的权重
-
中部抑制:中部80%的token计算损失时乘以0.5的权重
-
尾部抑制:尾部10%的token计算损失时乘以0.5的权重
实验发现,加权方法对比默认方法并没有明显优势,基本都取得了相当的效果,证实了现行默认的预训练方法已经足够有效。
结论与展望
1. 本文贡献
本文在Scaling Law的基础上,进一步提出了Temporal Scaling Law,从而实现在时间维度上分析和预测LLMs在预训练过程中的损失变化,从而助力研究者们更好地把握LLMs预训练趋势,提高调参效率。
本文通过研究不同模型规模和训练阶段下LLMs每个token位置的损失不平衡现象,发现损失模式遵循一个倒数关系,并提供了这种模式的数学化描述。
此外,本文通过Temporal Scaling Law揭示了LLMs在不同token位置的学习模式,尽管在初始训练阶段存在不同位置token的损失不平衡,但LLMs在经过一定量token的训练以后,会对所有token位置平等学习。以此为启发,本文也验证了默认的LLMs训练范式(不使用基于位置的重加权策略)的有效性,为LLMs的预训练提供了更深入的理解。
2. 当前挑战与未来展望
-
本文的研究主要着眼于以transformer decoder为底座的类GPT生成式模型,而没有对transformer encoder为底座的模型或混合专家模型(Mixed of Experts Models)进行探索,因此本文的结论可能并不能推广,还有待进一步验证。
-
本文的研究主要集中在预训练阶段。而其他情况,如持续预训练,有监督微调,迁移学习,并没有被包括在内。在这些方向上,也有待做进一步验证。
-
此外,本文仅在468M和1.2B两个规模的模型上进行了验证,并没有推广到更大尺度的LLMs上面,因此Temporal Scaling Law能否推广到更大的模型上还需要更充分的实验。