需求概述

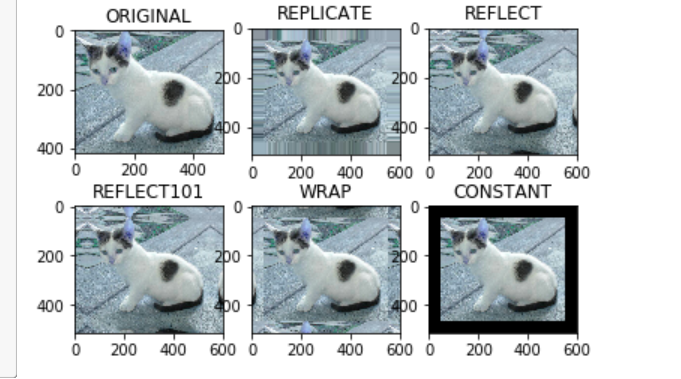
• 列表页展示列表，点击某个列表可以跳转到对应的详情页，点击上一页下一页可以按列表顺序跳转到对应详情页。
• 比如点击列表2进入到详情2，我点上一页可以跳转到详情1，点击下一页可以跳转到详情3。
• 难点：详情页如何按顺序切换
  
  

一开始我是从网上搜索答案，发现关于这部分的答案很少，所以自己思考了一下，总结了两个方案出来，有其他方法的可以评论区分享

方案1：id是按顺序递增递减

• 列表页思路：循环展示列表，点击携带id跳转到详情页；
• 详情页思路：根据传过来的id在数据列表中请求对应数据，上一页/下一页用类似/detail/id-1 / /detail/id+1的方式请求数据

缺点：id要是非递增顺序？而且除非第一个id是确定的，不然无法判断当前是第一/最后一页
js代码示例：

  /**
   * 上一页
   */
  prev() {
    if (this.currentIndex > 0) {
      this.currentIndex= this.currentIndex - 1
      // 获取对应详情数据
      this.getData(this.currentIndex)
    }
  },
  /**
   * 下一页
   */
  next() {
  // detailList是所有数据
    if (this.currentIndex < this.detailList.length - 1) {
      this.currentIndex=this.currentIndex + 1,
   	// 获取对应详情数据
      this.getData(this.currentIndex)
    }
  },

方案2:id乱序无规律

• 列表页思路：循环展示列表，点击携带id跳转到详情页；

• 详情页思路：

  • 1.获取所有id的详情数据，把所有id提取出来放在一个数组（或map）里面，
  • 2.根据传过来的id用indexOf获取此id数据列表中的下标索引index
  • 3.根据此id获取当前页面详情
  • 4.下一页：先用index==id数组.length判断是不是最后一页；用index+1获取下一个的id，获取对应详情；
  • 5.上一页：先用index==0判断是不是第一页；用index-1获取下一个的id，获取对应详情；

• 缺点：需要获取所有id然后检索，如果数据非常非常多，可能会卡顿