1 基本思路
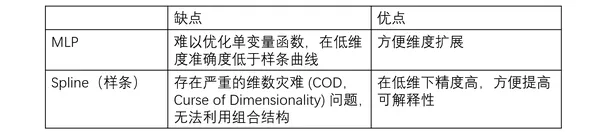
1.1 MLP与Spline的优缺点
多层感知器 (MLP)是深度学习的基础理论模块,是目前可用于逼近非线性函数的默认模型,其表征能力已由通用逼近定理证明。但MLP也有明显的缺点,例如在 Transformer中,MLP 的参数量巨大,且通常不具备可解释性。
为了提升表征能力,MIT提出了KAN。KAN本质上是样条(Spline)曲线和 MLP 的组合,吸收了两者的优点。即
KAN = MLP + Spline
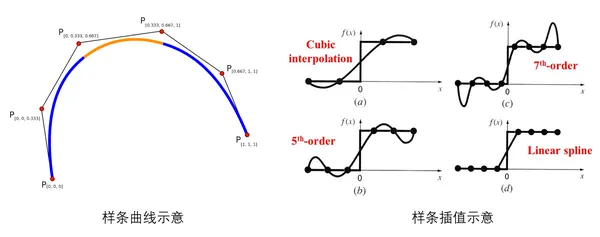
在数学中,样条曲线是由多项式分段定义的函数。一般的Spline可以是特定区间的3阶多项式。在插值问题中,样条插值通常优于多项式插值,因为即使使用低次多项式,也能产生类似的精度结果,同时避免了高次多项式的Runge's phenomenon(在一组等距插值点上使用高次多项式进行多项式插值时出现的区间边缘振荡问题)。
1.2 Kolmogorov-Arnold表示定理
Vladimir Arnold与 Andrey Kolmogorov证明了实分析中的如下表示定理:
如果f是多元连续函数,则f可以写成有限数量的单变量连续函数的两层嵌套叠加。其数学表达式就是
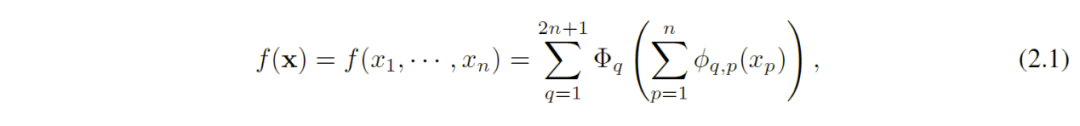
该定理解决了希尔伯特第十三问题的一个更受约束但更一般的形式。在数学上,Φq称外部函数(outer functions),Φq,p称为内部函数(inner functions)。
这表明在实数域上,唯一真正的多元函数是求和,因为所有其他函数都可以使用单变量函数求和来表征。
换个形象的说法,就是你家里做个复杂的事(包含多个任务),你爸你妈和你可以分别干活然后汇总,并不需要三个人同时忙一个任务。
顺带八卦下,Vladimir 是位前苏联神童, Andrey则是他的导师。
2 KAN架构与缩放
2.1 KAN架构
KAN的架构设计来自一个数学问题:对一个由输入输出对 {xi, yi} 组成的有监督学习任务,寻找函数f 使得所有数据点的 yi≈ f (xi)。其核心在于找到合适的单变量函数 Φq,p(外部函数)和 Φq(内部函数)。
在KAN中,使用B-spline(B样条)来构建。B-spline是基础样条(Basic Spline)的缩写。
对于B-spline,函数在其定义域内、在结点(Knot)都具有相同的连续性。其多项式表达可由Cox-de Boor 递推公式表达:
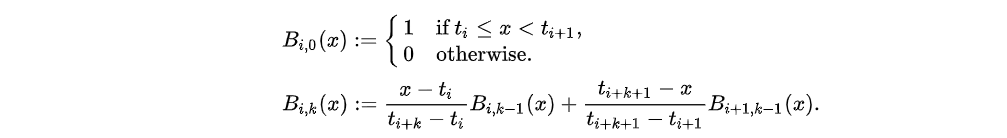
例如KA定理的内部函数可以定义为带有参数的矩阵计算。矩阵中的每个元素事实上是一个函数或算子。其中KAN层可以定义为
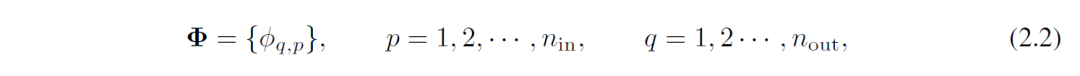
那么根据KA定理,理论上只要2个KAN层就可以充分表征实数域的各类有监督学习任务。2层的KAN中,激活函数放置在边缘而不是节点上(在节点上进行简单求和),并且2层中间有2n+1个变量。当然为了保证数值逼近的精度,实际设计中可以构建2层以上或者任意层数的KAN。
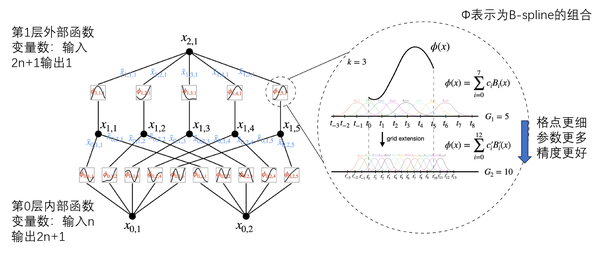
2层KAN的结构(作者团队修改自MIT)
更为一般的的KAN表征形式是:
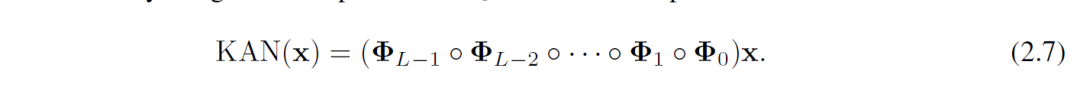
其中Φ l是第l个KAN层所对应的函数矩阵(B-spline函数矩阵),x为输入矩阵。
最简的KAN可以写为: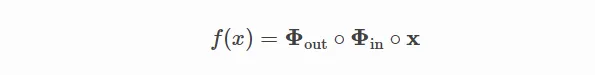
由于B-spline函数具备很好的可导性,因此在这里可以使用大家习惯的反向传播(BP)方法来进行KAN的训练。
2.2 架构细节
为了确保KAN实用,MIT团队还做了一些关键优化。
包括:
1)残差激活函数
使用一个基础(basis)函数 b(x)(类似于残差连接),使激活函数 Φ (x) 是基础函数 b(x) 和样条函数的和。
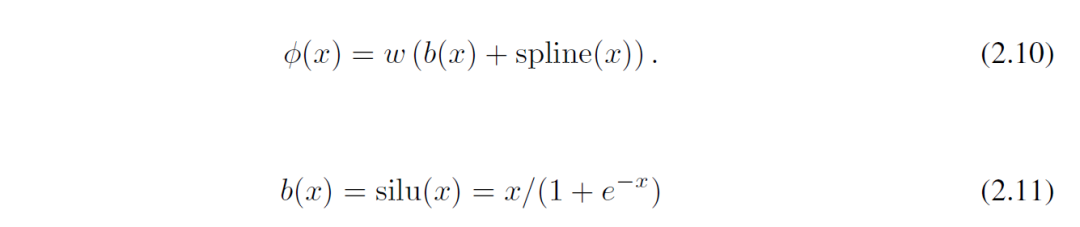
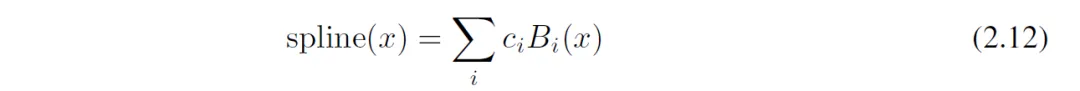
2)初始化方式
每个激活函数都被初始化为 spline(x) ≈ 0^2。 而w根据MLP 中的线性层的初始化方式进行。
3)Spline网格的更新
据输入激活动态更新每个网格,以解决Spline在有界区域上定义但激活值在训练期间可能超出出固定区域的问题。
2.3 KAN的逼近与神经缩放
关于KAN缩放的基本观点浓缩为以下2点:
1)2层的KAN表征可能是非平滑的,更深的KAN表征可以获得更平滑的逼近。
2)有限维度的KAN就可以很好的逼近样本函数。
下面我们来看看缩放定律:
神经缩放定律是测试损失(Loss)随着模型参数的增加而减小的现象,即 ℓ ∝ N_−α_,其中 ℓ 是测试 RMSE(均方根差),N 是参数数量,α 是缩放指数。也就是说,参数量越大,误差越小(精度越高)。
由于数据域的网格可以以任意的刻度进行细粒度化。因此B-spline曲线可以任意精确的达到(逼近)目标函数,而且这一优势被KAN继承了。
相比之下,MLP 没有“细粒度”的概念。(MLP一般不按数据分区进行训练)
对于 KAN,可以先训练一个参数较少的 KAN,然后通过使Spline网格粒度更细,使其扩展到参数较多的 KAN,这一方式降低了复杂度。
当然这一点可能也有一些问题,因为实际的AI芯片中并未对粒度计算提供太多的设计,激活函数个数越多,区间越细事实上会造成更大的存储带宽瓶颈。
3 KAN的可解释性
在解释之前,先通过稀疏正则化对KAN进行训练,然后剪枝。剪枝后的 KAN更容易解释。
MIT团队给出了解释KAN的基本流程:
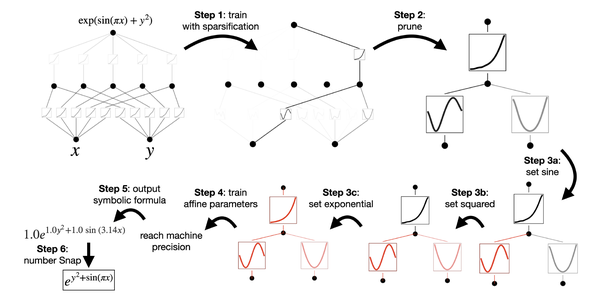
KAN的解释流程
1)稀疏化(Sparsification)(预处理)
对于KAN来说,
a) 线性权重被可学习的激活函数取代,因此需定义这些激活函数的 L1 范数,激活函数的 L1 范数定义为其 Np个输入的平均幅度;
b) 单独 L1范数 不足以实现 KAN 的稀疏化;还需要额外的熵正则化。
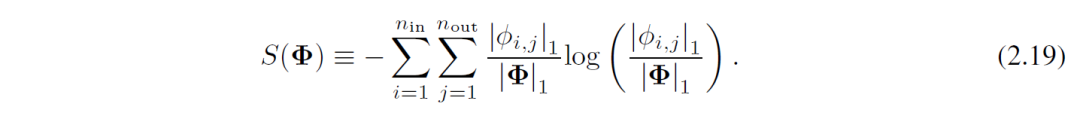
2)可视化(Visualization)
将激活函数 Φl,i,j的透明度设置为与 tanh(βAl,i,j) 成正比,其中 β = 3 。小幅度的函数被忽略以聚焦重要函数。
3)剪枝(Pruning)
经过稀疏化惩罚训练后,一般还需要将网络修剪成更小的子网。在节点级别对 KAN 进行稀疏化,所有不重要的神经元都被修剪。
4)符号化(Symbolification)
如果猜测某些激活函数实际上是符号函数(例如 cos 或 log),则提供一个接口将其设置为指定的符号形式,例如fix_symbolic(l,i,j,f) 可以设置 (l , i, j) 激活为 f 。从样本中获得预激活(Preactivation) x 和后激活(Postactivation) y,并拟合仿射参数 (a, b, c, d),使得 y ≈ cf (ax + b) + d。这里的拟合可通过 a、b 的迭代搜索和线性回归来完成。
4 小结
4.1 KAN的发展空间
KAN还有进一步优化的巨大空间,包括:
1) 准确性。KAN的精度优于传统MLP结构。一些替代方案有可能进一步提高准确性,例如,Spline激活函数可能被径向基函数或其他核函数替换,或者使用自适应网格策略。
2) 计算效率。 目前KAN 计算效率较低的主要原因是不同的激活函数进行批量计算(通过同一函数处理大量数据)。如果通过将激活函数分组为多个组,可以在全部相同(MLP)和不同(KAN)的激活函数之间进行插值,组内的成员共享相同的激活函数。
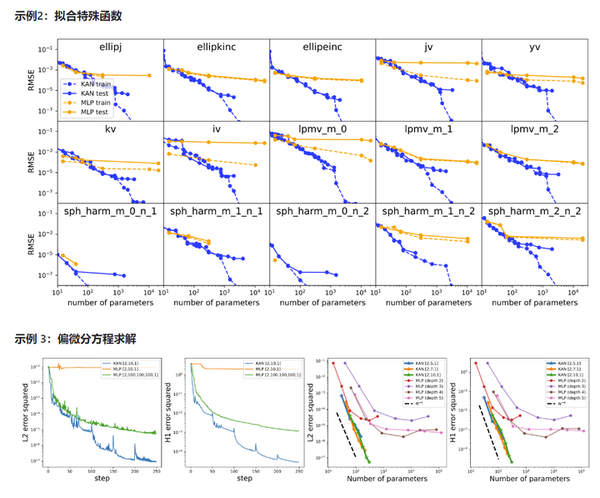
KAN准确性优于MLP
4.2 KAN的瓶颈
目前看,尽管KAN有很多优点,但其的最大瓶颈在于训练速度慢。根据MIT团队提供的信息,在参数数量相同的情况下,KAN 通常比 MLP 慢 10 倍。
由于训练算力限制,短期看KAN还是很难代替MLP的。如果想要获得类似Transformer架构的类似效果,走的路会更长,训练代价也要大很多。
长远看KAN可能逐渐在数学物理研究中广泛采用,然后逐渐进入主流舞台。
总体来说KAN的作者构建了一个非常好的基于KA定理的模型框架体系,并给出了足够的理论支撑,该文章估计会成为一代经典。
最后:
如果你想要进一步了解更多的相关知识,可以关注下面公众号联系~会不定期发布相关设计内容包括但不限于如下内容:信号处理、通信仿真、算法设计、matlab appdesigner,gui设计、simulink仿真......希望能帮到你!










![[GESP样题 四级] 填幻方和幸运数](https://img-blog.csdnimg.cn/direct/0f8daa2849034bf89f43c6b2bdff7327.png)