关键词:Quantum Wave Function
文章目录
- 一、说明
- 二、什么是波函数?
- 三 量子波的可视化
- 四、量子波的概率解释
一、说明
在量子力学中,粒子是我们只有在测量它们时才能看到的东西。其中运动模式由满足薛定谔方程的波函数描述。波函数并非量子力学所独有,它用于其他系统,例如水波纹的运动、声波、弦上的振动、电磁波等。这些系统中的每一个都有自己的波动方程,这些方程具有相似之处,因为它们都表示波函数在空间和时间上的变化。关键的区别在于量子波函数不是物理波。没有介质,所以没有办法用我们目前的知识证明它们是真实的,但它们很好地描述了量子粒子的行为。
二、什么是波函数?
在量子物理学中,波函数是对粒子量子态的数学描述,作为动量、时间、位置和自旋的函数。波函数的符号是希腊字母 psi,𝚿。
通过使用波函数,可以解释在物质波中找到电子的概率。这可以通过包含一个虚数来获得,该虚数被平方以获得实数解,从而得出电子的位置。波函数的概念是在薛定谔方程的帮助下于1925年提出的。
波函数是复值的。例如,波函数可能会为空间区域中的每个点分配一个复数。玻恩规则[ 1] [2] [3]提供了将这些复杂概率幅度转化为实际概率的方法。在一种常见的形式中,它表示取决于位置的波函数的平方模量是测量粒子位于给定位置的概率密度。波函数的平方模量对系统所有自由度的积分必须等于 1,这一条件称为归一化。由于波函数是复值,只能测量其相对相位和相对幅度;孤立地,它的值并不能说明可测量的可观察量的大小或方向。人们必须将量子算子(其特征值对应于一组可能的测量结果)应用于波函数ψ并计算可测量量的统计分布。
波函数可以是位置以外的变量的函数,例如动量。通过傅里叶变换,由取决于位置的波函数表示的信息可以转换为取决于动量的波函数,反之亦然。一些粒子,如电子和光子,具有非零自旋,并且此类粒子的波函数包括作为内在的离散自由度的自旋;还可以包括其他离散变量,例如isospin。当系统具有内部自由度时,连续自由度中每个点(例如,空间中的点)的波函数为离散自由度的每个可能值(例如,旋转)。这些值通常显示在列矩阵中(例如,自旋为1 ⁄ 2的非相对论性电子的2 × 1列向量)。

根据量子力学的叠加原理,波函数可以相加并乘以复数,形成新的波函数,形成希尔伯特空间。两个波函数之间的内积是对相应物理状态之间重叠的度量,用于量子力学的基础概率解释,即玻恩规则,将跃迁概率与内积联系起来。薛定谔方程决定了波函数如何随时间演化,并且波函数的行为在性质上与其他波(例如水波或弦上的波)类似,因为薛定谔方程在数学上是波动方程的一种。这解释了“波函数”的名称,并产生了波粒二象性。然而,量子力学中的波函数描述的是一种物理现象,截至2023年仍然有不同的解释,它与经典机械波的波函数有根本的不同。
三 量子波的可视化
因此,让我们做下一个最好的事情并可视化它!这是方程式,它取决于时间和空间的因素。
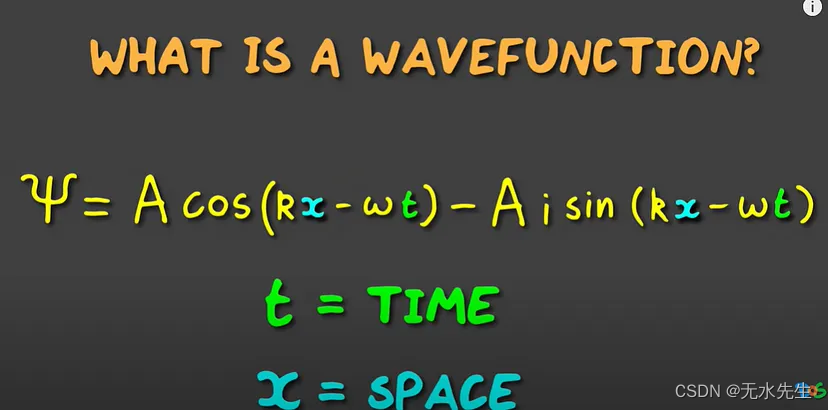
来源 — https://www.youtube.com/watch?v=sOI4DlWQ_1w
该方程使用 1 维空间,这是一种简化,因为真实粒子位于 3 维空间中,但这种简化允许我们绘制函数。所以让我们这样做吧。让我们从绘制第一项开始:
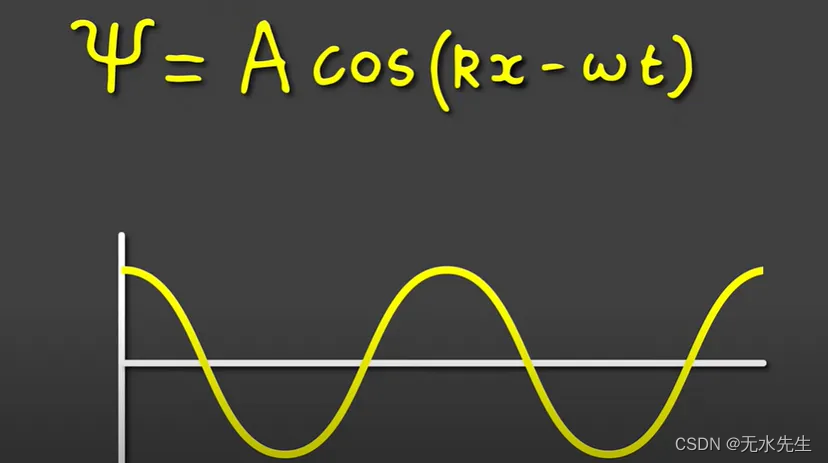
来源 — https://www.youtube.com/watch?v=sOI4DlWQ_1w
我们得到的只是一个余波。请注意,k 是控制波长大小的变量,omega 控制振荡频率,A 控制振幅。
为了绘制波浪的第二部分,即使波浪是一维的,我们也需要另一个轴。这是因为波函数的 sin 部分乘以虚数 i,这使它成为复波函数。
下图显示了两个独立绘制的波浪:
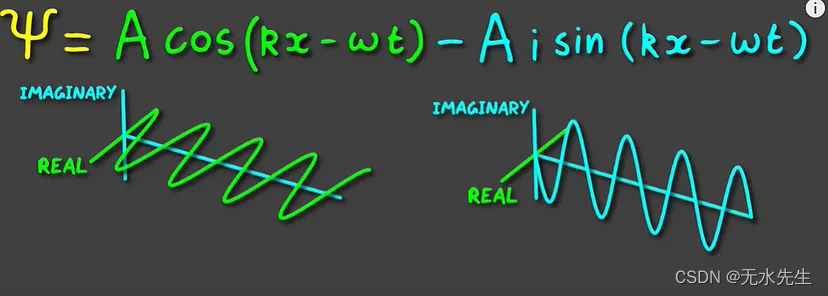
来源 — https://www.youtube.com/watch?v=sOI4DlWQ_1w
现在让我们看看当我们把整个事情放在一起时会发生什么:
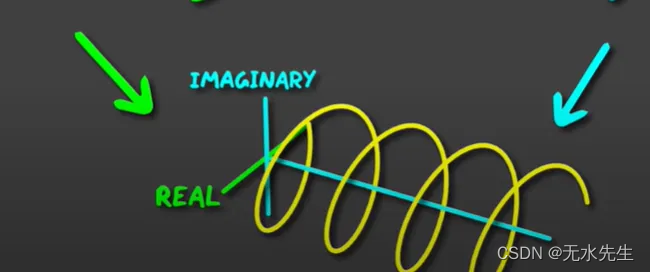
来源 — https://www.youtube.com/watch?v=sOI4DlWQ_1w
我们最终会得到从负无穷大到正无穷大的复杂值的螺旋式上升。下图固定在一个时间点,但如果时间继续移动,产生的波将围绕 x 轴振荡,类似于旋转线圈内部的条形。
四、量子波的概率解释
现在我们已经了解了量子波函数的样子,让我们来解决一个更有趣的问题。这是什么?
嗯,它被称为概率振幅,它本身并不是任何物理的东西,但如果你取振幅的模方,它会告诉你在这个一维空间中的任何时间点找到粒子的概率。它还通过对每个物理属性进行不同的数学运算来告诉您所有其他可测量的物理属性。
独立量子的波函数概率可视化:

总的来说,波函数是一种数学工具,它跟踪量子粒子的所有属性,并解释我们对粒子出现位置的概率性质的观察。
目前,我们只探索了一个波函数的例子,但还有更多的例子。他们只需要满足一组约束。
- 波函数必须是薛定谔方程的解
- 波函数必须是可归一化的:当您从波函数计算概率时,您将得到一个概率分布。这个分布的面积必须等于 1,因为你必须有一个确定的概率,你会在某个地方找到粒子。这意味着原始波函数不能具有无限面积。这意味着我们从技术上讲是不允许的,因为它从负无穷大到正无穷大。为了有效,它必须变为 0,因为 x 变为无穷大。
- 波函数必须是单值的。
- 它必须是连续的
- 波函数的斜率必须是连续的。
最后,让我们看一下超位置,它不是量子独有的属性。如果水中有两组重叠的涟漪,任何一点都会感觉到两个波相加。这是波浪的超级位置。在量子中,如果有两个或多个波函数是薛定谔方程的有效解,那么这些波函数的任意组合也是一个有效的解。这就是薛定谔的猫可以同时死去和活着的想法的来源。
尽管由于其他量子现象(例如纠缠和解相干)而从未真正发生过。这些概念以及爱因斯坦的EPR悖论将在以后的文章中探讨。

![[Cmake Qt]找不到文件ui_xx.h的问题?有关Qt工程的问题,看这篇文章就行了。](https://img-blog.csdnimg.cn/direct/4d470e5051ee4aa4918a1c7adee44b25.png)
![OSError: [WinError 1455] 页面文件太小,无法完成操作 的问题](https://img-blog.csdnimg.cn/direct/d52aea30ffa6436dae61333fdd4dcd34.png)