特征图尺寸和感受野是卷积神经网络中非常重要的两个概念，今天来看一下，如何计算特征尺寸和感受野。

特征图尺寸

卷积特征图，是图片经过卷积核处理之后的尺寸。计算输出特征的尺寸，需要给出卷积核的相关参数包括：

• 输入尺寸：输入图像或特征图的高度或宽度。
• 卷积核尺寸：卷积核的高度或宽度。
• 填充：应用于输入图像填充量。
• 步长：卷积核在输入图像上移动窗口。

首先计算卷积核能移动多少像素，直到卷积核不能在移动，输入尺寸 + 2 ×填充 − 卷积核尺寸，结果 / 步长，最后在加 +1， 加1 是可以理解为如果图像和卷积核尺寸一致，输出就是1 * 1。

输入 6 *6，卷积核 2 * 2， 步长 1， 填充 0，依据公式可得 （6 + 2 *0 - 2） / 1 + 1 =5。

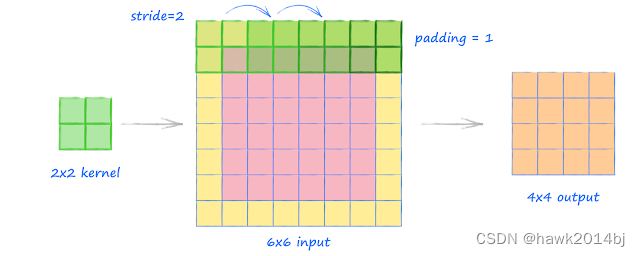
输入 6 *6，卷积核 2 * 2， 步长 2， 填充 1，依据公式可得 （6 + 2 *1 - 2） / 2 + 1 = 4。

感受野

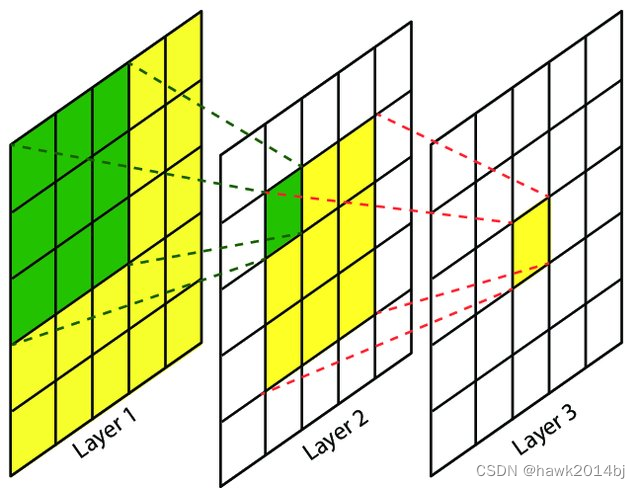
CNN 卷积神经网络有多层组成，特征图上能看到原始图的大小就是感受野，层数越多能观察到的信息也就越多。如下图，第二层感受野是 33，第三层的感受野是 55。

感受野公式：

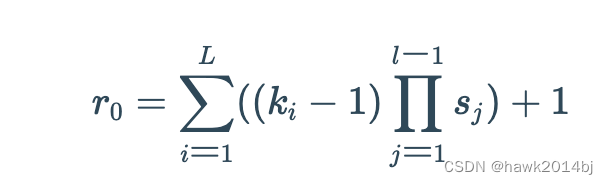
感受野的计算就是多层累加的过程，第一层就是卷积核的尺寸，第二层=第一层 + 第二层新增加边缘（卷积核尺寸-中心点）。如果步长大于 1，还要考虑步长的因素。
假设一个网络的前两层都使用了 3x3 的滤波器，步长为 1：

第一层：
	感受野 = 1 + (3 - 1) × 1 = 3
第二层：
对于第二层:
	感受野 = 3 + (3 - 1) × 1 = 5

假设一个网络的前三层都使用了 3x3 的滤波器，步长为 2：

第一层：
    卷积核大小 = 3，步长 = 2
    RF1=1+(3−1)×1=3

第二层：
    卷积核大小 = 3，步长 = 2
    此处，之前层的步长积仅为第1层的步长，即2。
    RF2=3+(3−1)×2=7

第三层：
    卷积核大小 = 3，步长 = 2
    第1层和第2层的步长积是 2×2=4。
    RF3=7+(3−1)×4=15