二、分析与设计

1. 二叉树：在这段代码中，我们使用了二叉树作为主要的数据结构。每个节点包含一个字符（数据）、一个频率（权重）以及指向左右子节点的指针。这种数据结构使我们能够有效地进行各种操作，如创建树、生成编码和计算WPL。
2. 优先队列：我们使用了优先队列（具有自定义比较函数的priority_queue）来帮助创建Huffman树。优先队列能够保证在任何时候，都能以对数时间复杂度获取（并删除）最小元素。
3. 哈希表：我们使用了哈希表（map）来存储字符到频率的映射（在创建Huffman树时）以及字符到Huffman编码的映射（在生成Huffman编码时）。

算法思想：

1. Huffman编码：Huffman编码是一种用于无损数据压缩的贪心算法。该算法使用字符的频率信息来构建一个最优的前缀编码，使得频率高的字符有更短的编码，频率低的字符有更长的编码，从而达到压缩数据的目的。
2. 深度优先搜索：在生成Huffman编码和计算WPL时，我们使用了深度优先搜索（DFS）。DFS是一种用于遍历或搜索树或图的算法。这种算法会尽可能深地搜索树的分支。在这里，我们使用DFS来遍历Huffman树，并在遍历过程中生成Huffman编码或计算WPL。
3. 递归：在多个地方，我们使用了递归的方法，如在DFS中遍历二叉树，以及在计算WPL时递归地计算子树的WPL。递归是一种将问题分解为更小子问题的方法，直到问题可以直接解决为止。

（2）设计表示：

主程序各子函数：

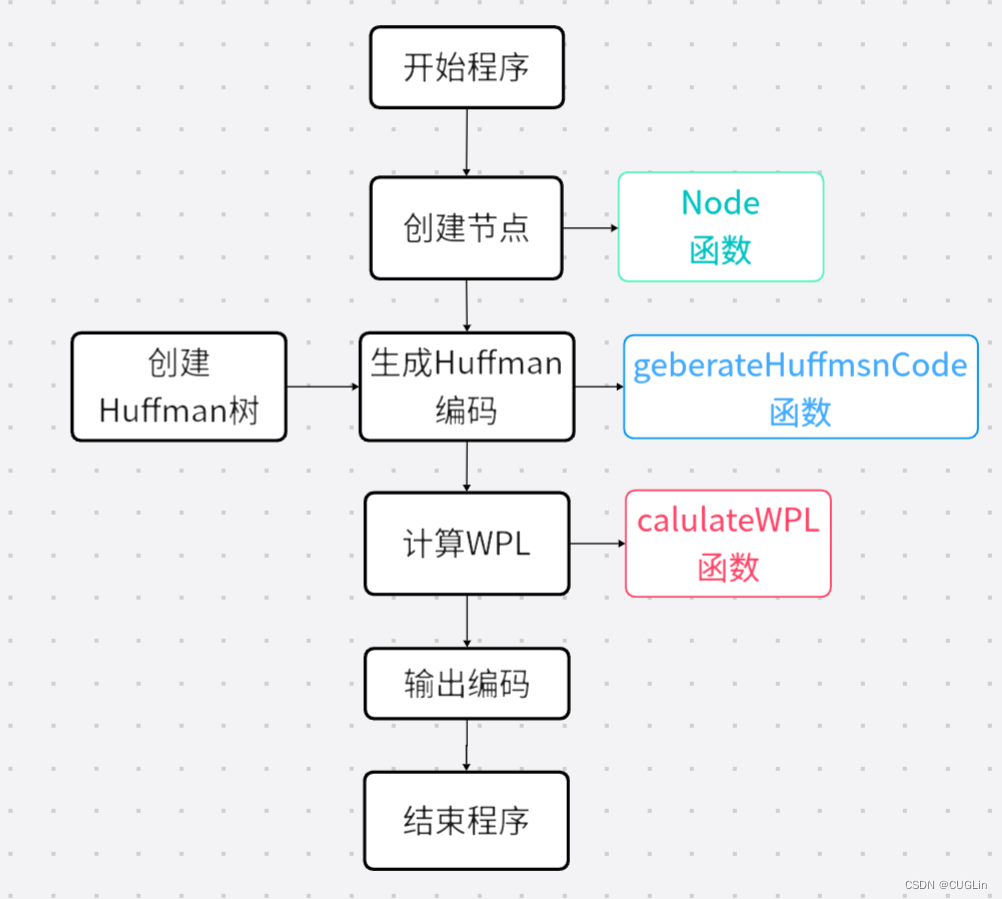
图1 函数调用流程图

三、编码说明

完整代码展示：

#include <iostream>
#include <fstream>
#include <vector>
#include <map>
#include <queue>
using namespace std;

// 定义节点类
class Node {
public:
    char data;  // 字符
    int freq;  // 频率
    Node* left;  // 左子节点
    Node* right;  // 右子节点

    Node(char data, int freq) {
        this->data = data;
        this->freq = freq;
        left = right = nullptr;
    }
};

// 定义比较类
class Compare {
public:
    bool operator()(Node* l, Node* r) {
        return l->freq > r->freq;
    }
};

// 定义Huffman树类
class HuffmanTree {
private:
    Node* root;  // Huffman树的根节点

    // 生成Huffman编码的方法
    void generateHuffmanCode(Node* root, string str, map<char, string>& huffmanCode) {
        if (root == nullptr)
            return;
        if (!root->left && !root->right) {
            huffmanCode[root->data] = str;
        }
        generateHuffmanCode(root->left, str + "0", huffmanCode);
        generateHuffmanCode(root->right, str + "1", huffmanCode);
    }

    // 计算WPL的方法
    int calculateWPL(Node* root, int depth) {
        if (root == nullptr)
            return 0;
        if (!root->left && !root->right)
            return depth * root->freq;
        return calculateWPL(root->left, depth + 1) + calculateWPL(root->right, depth + 1);
    }

public:
    // 创建Huffman树的方法
    map<char, int> createHuffmanTree(string text) {
        map<char, int> freqMap;
        for (char ch : text) {
            freqMap[ch]++;
        }

        priority_queue<Node*, vector<Node*>, Compare> pq;
        for (auto pair : freqMap) {
            pq.push(new Node(pair.first, pair.second));
        }

        while (pq.size() != 1) {
            Node* left = pq.top(); pq.pop();
            Node* right = pq.top(); pq.pop();

            int sum = left->freq + right->freq;
            Node* newNode = new Node('\0', sum);
            newNode->left = left;
            newNode->right = right;
            pq.push(newNode);
        }

        root = pq.top();
        return freqMap;
    }

    // 生成Huffman编码的方法
    map<char, string> generateHuffmanCode() {
        map<char, string> huffmanCode;
        generateHuffmanCode(root, "", huffmanCode);
        return huffmanCode;
    }

    // 计算WPL的方法
    int calculateWPL() {
        return calculateWPL(root, 0);
    }
};

int main() {
    HuffmanTree huffmanTree;
    string text;
    string filename;
    cout << "请输入文件名：";
    cin >> filename;  // 从键盘读取文件名

    // 从文件读取字符串
    ifstream file(filename, ios::binary);
    if (file.is_open()) {
        text = string((istreambuf_iterator<char>(file)), istreambuf_iterator<char>());
        file.close();
    }
    else {
        cout << "无法打开文件" << endl;
        return 1;
    }

    // 创建Huffman树并统计每个字符出现的频率
    map<char, int> freqMap = huffmanTree.createHuffmanTree(text);
    cout << "字符频率：" << endl;
    for (auto pair : freqMap) {
        cout << pair.first << ": " << pair.second << endl;
    }

    // 输出每个字符的Huffman编码
    map<char, string> huffmanCode = huffmanTree.generateHuffmanCode();
    cout << "Huffman编码：" << endl;
    for (auto pair : huffmanCode) {
        cout << pair.first << ": " << pair.second << endl;
    }

    // 计算并输出WPL
    int wpl = huffmanTree.calculateWPL();
    cout << "WPL: " << wpl << endl;

    return 0;
}

1. 文件读取：在最初的版本中，我发现程序无法从文件中读取字符串，只能接受键盘输入。这限制了程序的灵活性，因为用户可能希望直接从文件中读取数据，而不是手动输入。
2. 版本迭代：为了解决上述问题，我进行了第二次迭代，修改了代码以支持从文件中读取字符串。这个改进使得程序能够处理更复杂的情况，提高了其实用性。

通过这两个版本的迭代，我最终得到了一个可以从文件中读取字符串的程序。虽然这个过程中遇到了一些困难，但每一个挑战都使我有机会学习和成长，也使得最终的程序更加强大和灵活。

四、程序分析

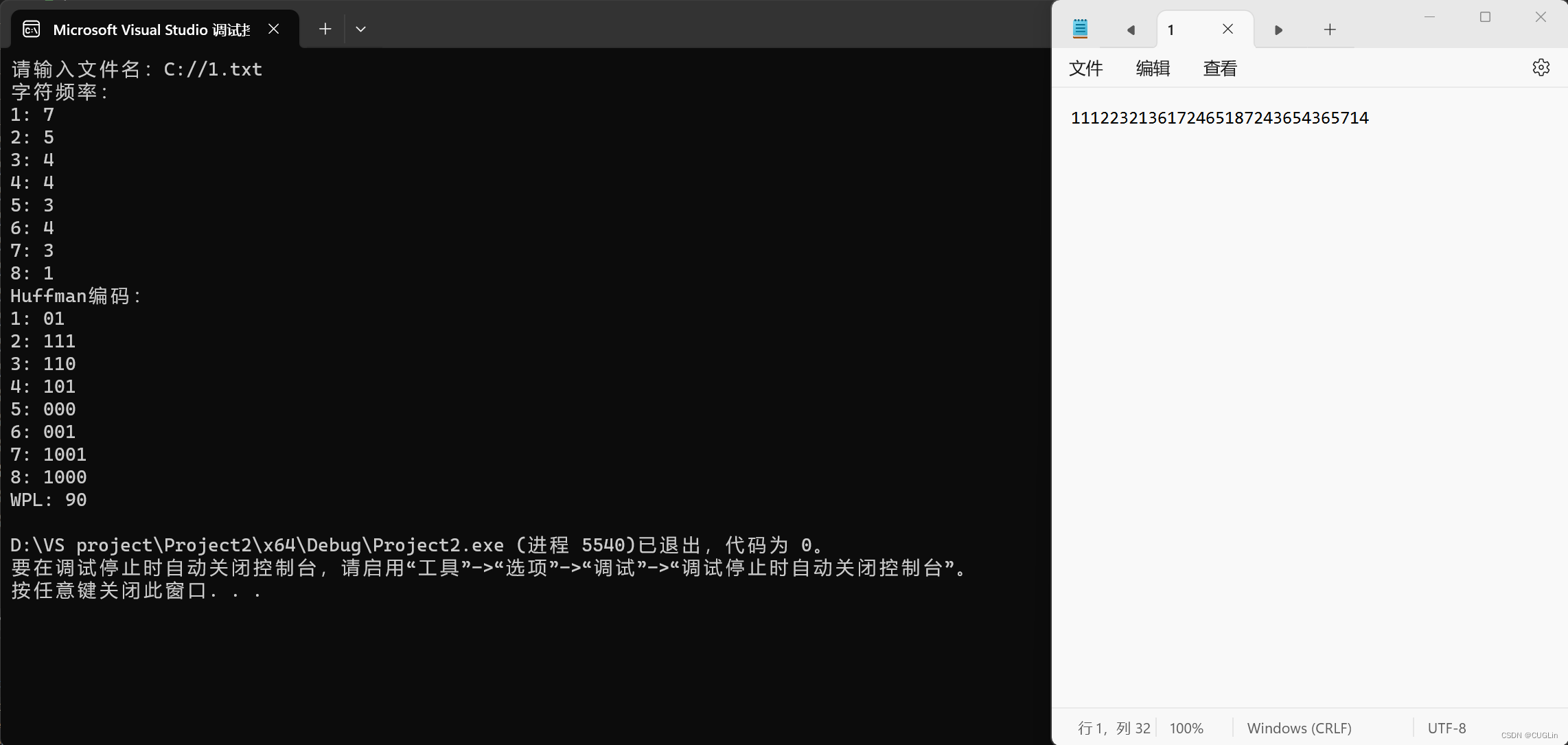
图2 运行结果图

1.时间复杂度：创建Huffman树的时间复杂度是O(n log n)，其中n是字符的种类数。这是因为我们需要n次插入操作和n-1次删除操作，每次操作的时间复杂度都是O(log n)。生成Huffman编码和计算WPL的时间复杂度都是O(n)，因为我们需要遍历整个Huffman树。

2.空间复杂度：在整个过程中，我们需要存储整个Huffman树，所以空间复杂度是O(n)。此外，我们还需要额外的空间来存储字符到频率的映射和字符到Huffman编码的映射，但这些空间的大小都是常数，所以不影响总的空间复杂度。

五、小结

在解决这个问题的过程中，我深刻地体会到了数据结构，尤其是Huffman树，在解决实际问题中的重要性。Huffman树这种特殊的二叉树结构，以其独特的优雅和高效性，给我留下了深刻的印象。通过这个挑战，我对Huffman树的构建、遍历、修改和查找等操作有了更深入的理解。

我要向我的数据结构老师，表达我最深的感谢。是她的悉心教导让我对数据结构有了深入的理解。她充满热情的教学和专业的知识激发了我对数据结构的热爱，并在我解决这个问题的过程中给予了我宝贵的指导。

此外，我要感谢数据结构这门课程。通过学习这门课程，我不仅掌握了如何更有效地组织和处理数据，还学会了如何分析和解决问题。这个过程对我产生了深远的影响，使我对计算机科学有了更深入的理解。

在解决问题的过程中，我也意识到了一些可以改进的地方。例如，我在创建Huffman树的过程中，未能充分考虑到用户可能输入无效的前序序列。未来，我将对我的代码进行改进，增加对用户输入的验证，以确保创建的Huffman树的有效性。

通过解决这个问题，我对Huffman树有了更深的理解，我的编程技能也得到了提升。在未来，我将继续深入学习和探索数据结构，以更好地应对各种实际问题。再次感谢我的数据结构老师和这门课程，让我有机会领略到数据结构的魅力！