各位看官们好,当我写了上一篇博客杨辉三角后,有一些看官叫我讲一下斐波那契数列。对于这个大家应该是有了解的。最简单的规律就是f(n)=f(n-2)+f(n-1)。就是当前是前两项之和,然后下标1和0都是1.从第三项开始计算的。那么我们知道规律,那么我们就直接来讲讲如何实现和实现方法有哪些吧。
递归
我想大家学习C语言到现在应该看到斐波那契数列应该想到的是递归吧。我想递归大家应该还知道它的核心思想吧,就是每递归一次,那么这个问题就要越靠近我们想要的答案一次,一直递归到想要答案就返回。好,那么我们现在想一想怎么搞。那么我们知道我们有特殊情况就是,如果我输入1和2的话,那么我们得到的值是1.那么我们这个就可以直接写出来哇。好当我们写出了特殊情况后,我们来思考正常情况。那么我们也知道我们规律就是前两项之和。那么我们就直接写啊,是不是。大家思考一下: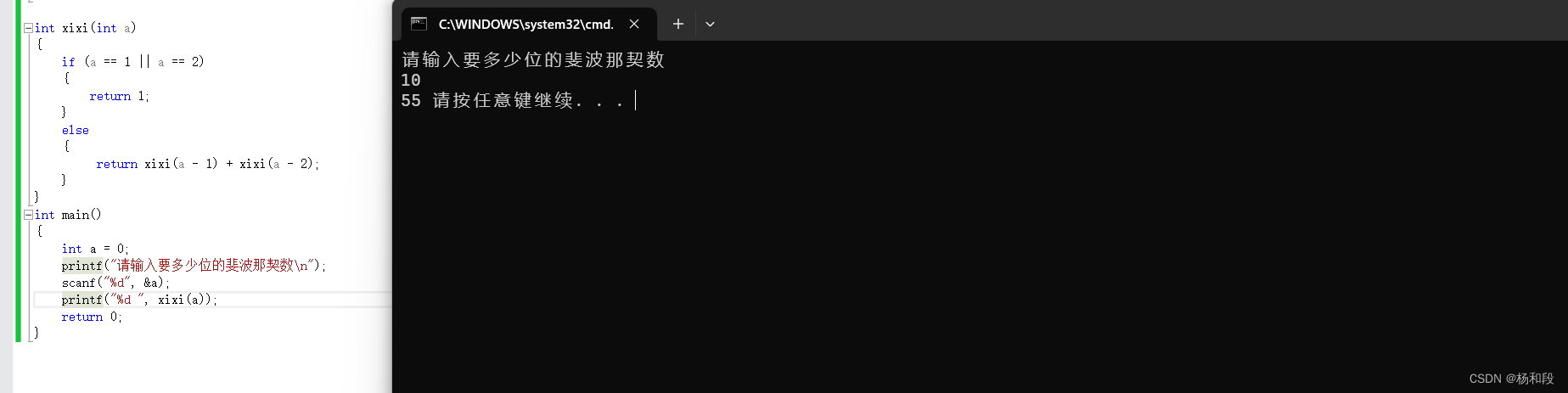
我们只要不是特殊情况的话,我们只需要在递归的时候将前两项传来,直到设定的值,那么我们就可以得到结果了。大家思考一次,是吧。代码很简单,但是有一个问题就是。递归的内存占用太多了。很有可能造成栈溢出。也许大家输入前面的数字编译器还是很快的输出的。但是当我们输入较大值如100这类的我们就可以明显的感觉速度很慢了。所以递归大家可以知道这个方法但是使用起来限制还是很大了。大家知道有这个办法就可以了。
for循环
okok,当我们写了递归后,我们递归其实还是有点难度的,毕竟我们还是需要思考一下,怎么实现的吧。但是我们要是用for循环的,我们从最开始学习C语言的时候我们就知道有个for循环。那么最基础的知识其实是很有作用的,那么我们来思考一下for循环如何来实现我们的斐波那契数吧。但其实for循环也是比较简单的,毕竟大家思考一下。我们最基本的规律就是前两项之和f3,那么我们就创建三个变量吧。一个作为最后的相加项我们最后返回的。然后另外两个就一个作为前一项f1一个作为前两项f2。那么这个如何交换值值嘞。首先我们就最开始的时候考虑特殊情况。1和2的时候那么我们就直接从2开始吧,如果我输入的值是1或者2的话,for本来就等于2了,不执行,然后直接返回f3。那么我们可以确定了f3的初始值为1吧。并且我们现在把特殊情况也处理了。那我们正常的话f3=f1+f2。然后f2=f3。这个是为什么嘞,因为我们大家算f3,是不是就是我们的前一个f3加一个f2但我不能直接写f3的前一项啊。所以f2就成为上一个f3吧。那f2成为上一个f3那。f1自然而然的变成了上一个的f2了吧。这样大家是不是就通透了呀。我们将f1,2,3全部设为1.然后for循环从2开始那么就排除了特殊情况。然后最开始就将f3更新,然后f2和f1相继跟新这样如果下次没有更新的话,我们就可以直接确定了返回值f3了。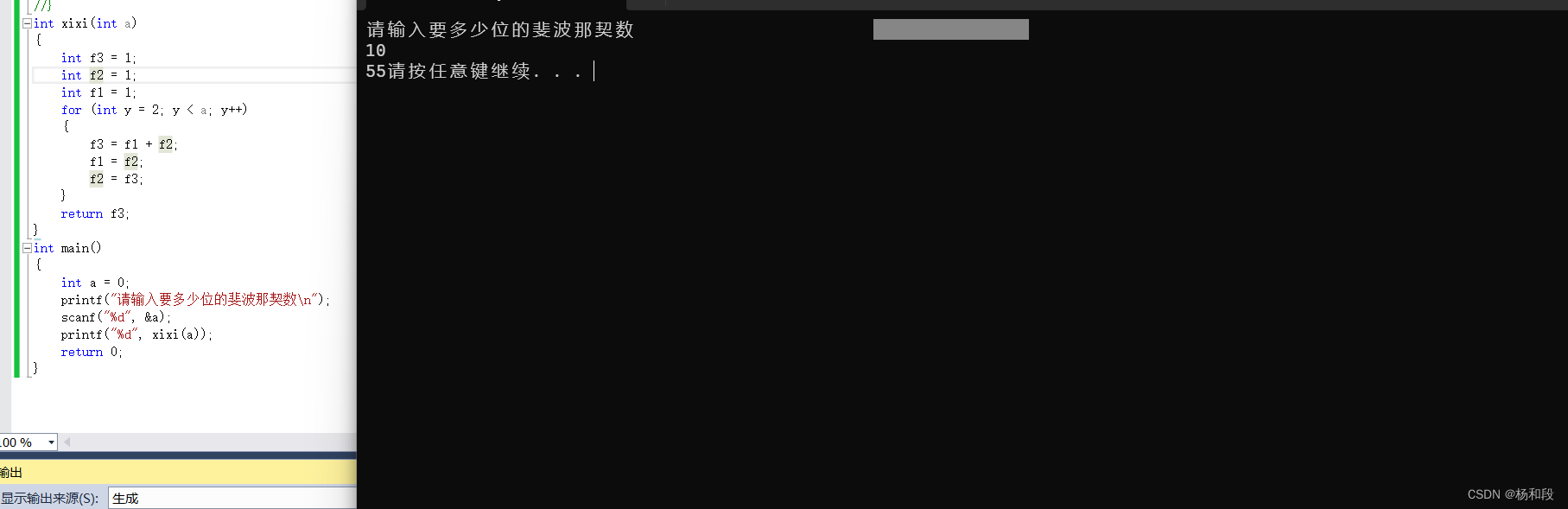
大家需要注意一下啊。就是f1与f2更新的顺序不要乱哦。不然的话f1也变成上一个f3了。然后就太多的麻烦了。
数组
OK呀,其实讲了上面的两个方法就差不多了的,但是我还想到了一个方法,就是我们使用数组来实现这个。那大家先想一想数组如何实现这个了。但其实啊。也很简单与我们的for循环是差不多的。我们上一个for循环是需要实时更新的,但我们数组其实就是很简单的。我们创建一个较大的数组。然后没循环一次,那么就往数组里写入新的值,然后循环到设定值结束,那么就返回这个数组下标的的元素就可以了。那么简单的思路那我们就直接开始搞吧。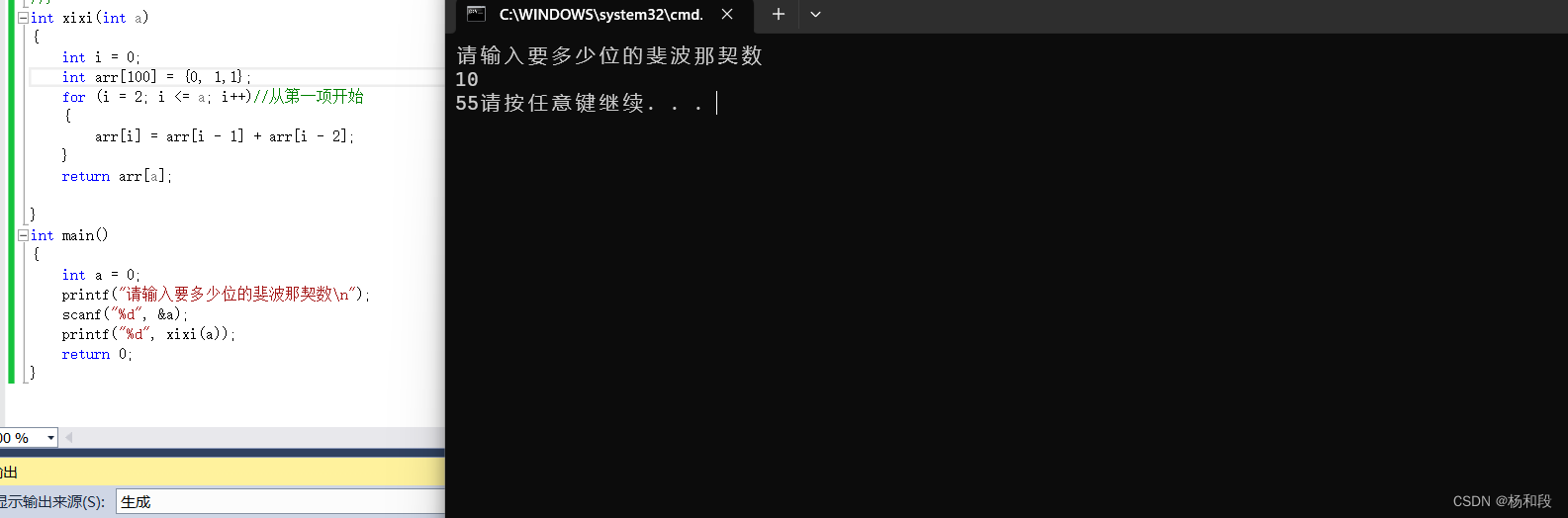
大家看看上面咦。为什么我们创建数组的时候开始要给0,1,1的值啊。其实也很简单就是我们数组下标啊。我们原本计算的都是从1开始的,但是我们数组是下标如果不设置得话,那么下标0为1,设置的值就会大很多,当然是越向后值就比正确值大很多。大家可以下来尝试一下。
好了,那么我们上面三种方法就差不多了,递归方法虽然有,但是可以处理小部分递归次数较小的,如果太大了。那么就是会很慢甚至报错。建议少用用for循环的方法也可以。好了。以上就是本篇博客的内容了。如果还有补充的话,希望大家可以评论区留言。