Matten: Video Generation with Mamba-Attention

摘要

在本文中，作者介绍了Matten，一种具有Mamba-Attention架构的尖端潜在扩散模型，用于视频生成。在极小的计算成本下，Matten利用空间-时间注意力对局部视频内容进行建模，并使用双向Mamba对全局视频内容进行建模。

作者的全面实验评估表明，Matten在基准性能上与当前的基于Transformer和GAN的模型具有竞争力，实现了更优的FVD得分和效率。

此外，作者观察到作者设计的模型复杂度与视频质量的提升之间存在直接的正相关关系，这表明Matten具有出色的可扩展性。

Introduction

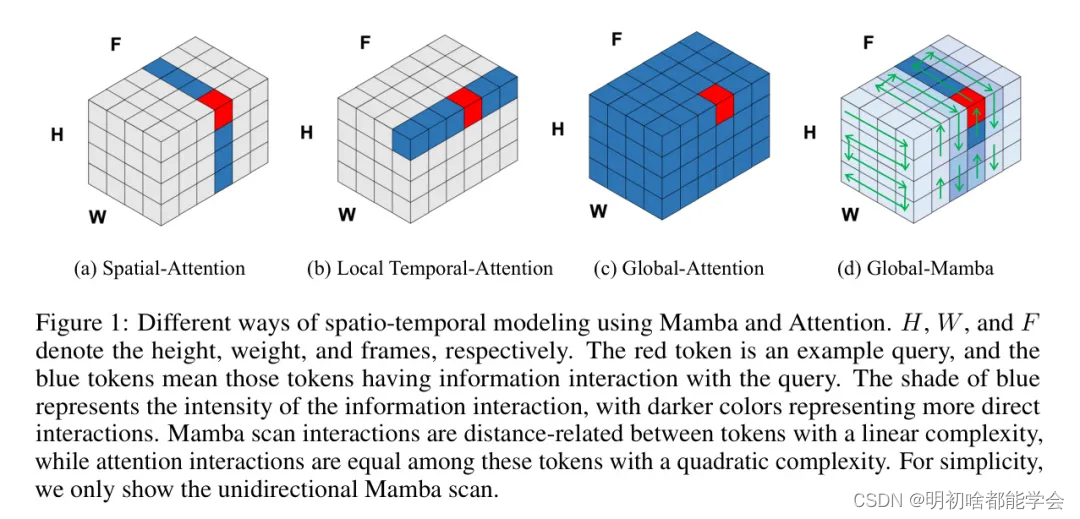
近期在扩散模型方面的进展已经在视频生成方面显示出令人印象深刻的能力。已经观察到，在架构设计上的突破对于这些模型的有效应用至关重要。当代研究主要集中在基于CNN的U-Net架构和基于Transformer的框架上，这两种方法都采用注意力机制来处理视频内容中的时空动态。如图1（a）所示，空间注意力在基于U-Net和基于Transformer的视频生成扩散模型中被广泛使用，它涉及在单帧内的图像标记之间计算自注意力。现有技术通常在时间层内应用局部注意力，如图1（b）所示，其中注意力计算被限制在不同帧中相同位置上。这种方法未能解决捕捉连续帧中不同空间位置间相互关系的关键方面。如图1（c）所示，对于时空分析的一种更有效方法是将不同空间和时间位置的交互进行映射。然而，由于计算注意力的二次复杂度，这种全局注意力方法是计算密集型的，因此需要大量的计算资源。

在各种领域中，状态空间模型（SSMs）的兴趣日益增长，这主要归功于它们处理长序列数据的能力。

在自然语言处理（NLP）领域，像Mamba模型这样的创新通过在SSM结构中引入动态参数，并构建针对硬件兼容性更好的算法，显著提高了数据推理过程的效率和模型的总体性能。

Mamba框架的实用性已成功扩展到其最初应用之外，证明了其在视觉和多模态应用等领域的有效性。

鉴于处理视频数据的复杂性，作者 Proposal 使用Mamba架构来探索视频内容中的时空交互，如图1（d）所示。然而，值得注意的是，与自注意力层不同，Mamba扫描（本质上不计算标记间的依赖关系）在有效检测局部数据模式方面存在困难，这是[15]指出的局限性。

鉴于Mamba和注意力的优点，作者提出了一种名为Matten的视频生成潜在扩散模型，该模型采用Mamba-Attention架构。具体来说，作者研究了Mamba和注意力机制各种组合对视频生成的影响。作者的研究结果表明，最有效的方法是使用Mamba模块捕捉全局时间关系（图1（d）），同时使用注意力模块捕捉空间和局部时间关系（图1（a）和图1（b））。

作者进行了实验评估，以检查Matten在无条件和有条件视频生成任务中的性能和效果。在所有测试基准中，Matten始终显示出与SOTAs相当的视频生成质量（FVD评分[16]）和效率。此外，作者的结果表明Matten是可扩展的，这通过模型复杂性与生成样本质量之间的直接正比关系得到了证明。

总之，作者的贡献如下：

1. 作者提出了Matten，这是一种集成了Mamba块和注意力操作的新型视频潜在扩散模型，它能够高效且优越地进行视频生成。
2. 作者设计了四种模型变体，以探索在视频生成中Mamba和注意力的最佳组合。基于这些变体，作者发现采用注意力机制捕捉局部时空细节，并利用Mamba模块捕捉全局信息的途径是最有利的。
3. 综合评估显示，作者的Matten在计算和参数要求较低的情况下与其他模型取得了相当的性能，并显示出强大的可扩展性。

Related Work

Video Generation
视频生成的主要任务在于产生具有高质量视觉和流畅动作的真实视频片段。此前的视频生成工作可以归纳为三种类型。最初，许多研究者专注于将强大的基于GAN的图像生成技术适配于视频创作。然而，基于GAN的方法可能导致模式崩溃，减少多样性和真实性。
图1：使用Mamba和注意力进行时空建模的不同方式。H、W和F分别代表高度、宽度和帧数。红色标记是一个示例 Query ，蓝色标记意味着与 Query 具有信息交互的标记。蓝色的深浅表示信息交互的强度，颜色越深表示交互越直接。Mamba扫描交互具有线性复杂度，基于标记之间的距离相关；而注意力交互在这些建立标记之间是等价的，具有二次复杂度。为了简化，作者只展示了单向Mamba扫描。

此外，某些模型建议通过自回归模型学习数据分布。这些方法通常能产生高质量的视频，并显示出更可靠的收敛性，但受到其巨大的计算需求的限制。最后，视频生成领域的最新进展集中在开发利用扩散模型的系统，这些模型已显示出巨大的潜力。这些方法主要使用基于CNN的U-Net或Transformer作为模型架构。与这些工作不同，作者的方法专注于在视频扩散中探索结合Mamba和注意力的未被充分研究的领域。### Mamba

Mamba，一种新的状态空间模型，因其通用逼近能力和对长序列的高效建模，最近在深度学习中受到了关注，应用领域包括医学成像、图像恢复、图形、自然语言处理和图像生成。借鉴控制系统，并利用HiPPO初始化[41]，这些模型（如LSSL[11]）解决了长距离依赖问题，但受到计算需求的限制。为了克服这一点，S4和其他结构化状态空间模型引入了各种配置和机制[10]，这些已被整合到更大的表示模型中，用于语言和语音任务。Mamba及其迭代版本，如VisionMamba，S4ND[48]，和Mamba-ND[49]，展示了从双向SSM到局部卷积和多维考虑的计算策略。对于3D成像，T-Mamba[50]利用Mamba处理长距离依赖的强大能力，解决了正畸诊断中的挑战。在视频理解领域，VideoMamba和Video Mamba Suite[52]将Mamba适配到视频领域，并解决了视频数据中普遍存在的局部冗余和全局依赖的挑战。在利用mamba进行扩散应用领域，Zigzag Mamba[53]提高了生成视觉内容的可扩展性和效率。它采用创新的扫描方法解决了空间连续性的关键问题，融合了文本条件特征，并在高分辨率图像和视频数据集上显示了性能的增强。[54]与作者的工作密切相关，在视频扩散的时间层中使用mamba块。与之前主要关注局部时间建模的研究不同，作者的方法Matten独特地设计为涵盖全局时间维度。

Methodology

作者的讨论从第3.1节对潜在空间扩散模型和状态空间模型的简要概述开始。接着在第3.2节深入描述了Matten模型变体。然后在第3.3节探讨了与时间步或类别相关的条件方法。最后，在第3.4节中，作者呈现了对Mamba与注意力机制进行比较的理论分析。
Background
潜在空间扩散模型[55]。对于输入数据样本$a\in P_{\text{data}}(z)$，潜在扩散模型(LDMs）首先使用预训练的VAE或VQ-VAE编码器，将数据样本转换为潜在表示$z=E(a)$。这种转换之后是一个学习阶段，通过扩散和去噪步骤对数据分布进行建模。

在扩散阶段，逐渐向潜在编码中添加噪声，产生一系列逐渐被扰动的潜在状态 $z$，其中附加噪声的强度由时间步长$t\in T$表示。一个特殊的模型，如U-Net，被用作噪声估计网络，在去噪阶段估计影响潜在表示$z$的噪声扰动，旨在最小化潜在扩散目标。

简单地说，$E(z\sim p(z)),e\sim N(0,I),t\le t_0(zt,t)$。

此外，扩散模型$g$通过学习逆向过程协方差进行增强，使用$L_{lh}$进行优化，如[6]所述。

在作者的研究中，c日是使用基于Mamba的框架设计的。同时使用$L_{\text{simple}}$和$L_{\text{olb}}$来提高模型的有效性和效率。

状态空间Backbone网络。状态空间模型(SSMs)已经通过理论和实证研究被严格验证能够很好地处理长距离依赖，显示出与数据序列长度成线性扩展的能力。传统上，线性状态空间模型表示为以下类型:

$h^{\prime }(t)=A(t)h(t)+B(t)z(t)，g(t)=C(t)h(t)+D(t)z(t)$，

该模型描述了一个一维输入序列$a(t)\in \mathbb{R}$转换为一个一维输出序列$g_y(t)\in \mathbb{R}$的过程，通过一个$N$维潜在状态序列$h(t)\in {\mathbb{R}}^N$进行调节。状态空间模型特别设计用于在神经序列建模架构中集成这些基本方程的多个层次，允许每一层的参数$A,B,C$和$D$通过深度学习损失函数进行优化。$N$表示状态大小，$A\in {\mathbb{R}}^{N\times N}$，$B\in {\mathbb{R}}^{N\times 1}$，$C\in {\mathbb{R}}^{1\times N}$，以及$D\in \mathbb{R}$。
将状态空间模型应用于现实世界的深度学习任务时，如方程式2中详细描述的，离散化过程至关重要，它将连续系统参数如$A$和$B$转换为它们的离散等效参数$A$和$B$。这一关键步骤通常采用零阶保持（ZOH）方法，这一技术在学术研究中因其有效性而广为人知。ZOH方法使用时间尺度参数$\Delta$来弥合连续和离散参数之间的差距，从而促进理论模型在计算设置中的应用。

$A=\text{exp}(A\Delta ),B=(A\Delta {)}^{-1}(\text{exp}(A)-I)\cdot AB$.

使用这些离散化参数，方程式2中概述的模型然后适应使用时间步长$\Delta$的离散框架:

$h_k=A{h}_{k-1}+B{x}_k，y_k=C{h}_k+D{z}_k$.

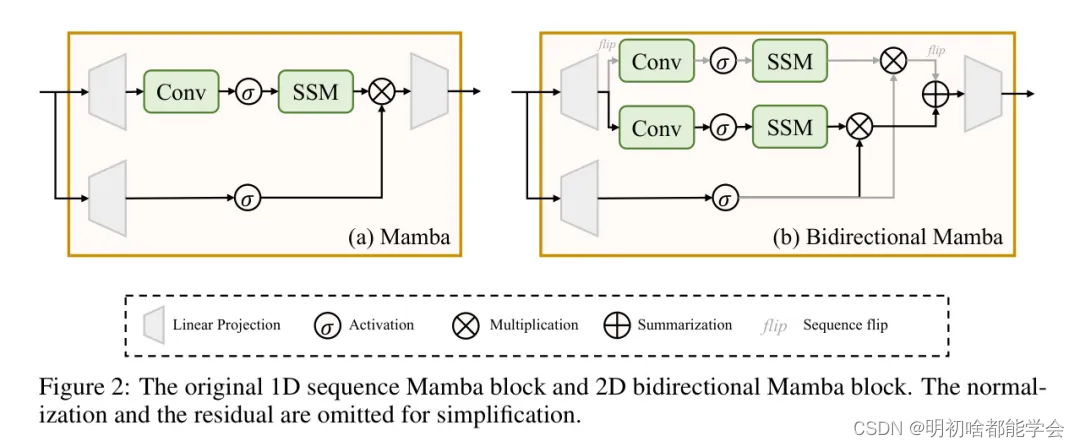
这种方法允许将状态空间模型无缝集成到数字平台中。最初为1D序列处理设计的传统Mamba块（如图2所示）并不非常适合需要空间认知的视觉任务。为了解决这一限制，Vision Mamba[13]开发了一种专门针对视觉相关应用的双向Mamba块。这个创新的块通过同时使用前向和后向SSM来处理展平的视觉序列，显著提高了其处理空间感知的能力。

Mamba采用了一种工作高效的并行扫描，有效地减少了通常与递归计算相关的顺序依赖性。这种优化，结合GPU操作的战略性利用，消除了明确管理扩展状态矩阵的必要性。在作者的研究中，作者探讨了将Mamba架构集成到视频生成框架中，利用其效率和可扩展性。
The Model Variants of Matten
考虑视频片段潜在空间的表示，由$V_L\in {\mathbb{R}}^{F\times H\times W\times C}$表示，其中$F$指示帧数，$H$是帧的高度，$W$是帧的宽度，$C$是视频潜在配置中每帧的通道数。作者将$V_L$转换为一系列Token，通过分段和Reshape它，表示为$z\in {\mathbb{R}}^{(n_f\times T_h\times T_w)\times 4}$。在这里，$n_f\times T_h\times T_w$表示Token的总数，每个Token具有维度$d$。
采用类似于Latte的策略，作者分配$n_f=F,n_h=H/2,n_w=W/2$以有效地构造数据。此外，一个时空位置嵌入，记为$p$，被合并到Token序列$z$中。因此，Matten模型的输入变为$z=z+p$，这有助于复杂的模型交互。如图3所示，作者引入了Matten模型的四个不同变体，以增强其在视频处理中的适应性和有效性。

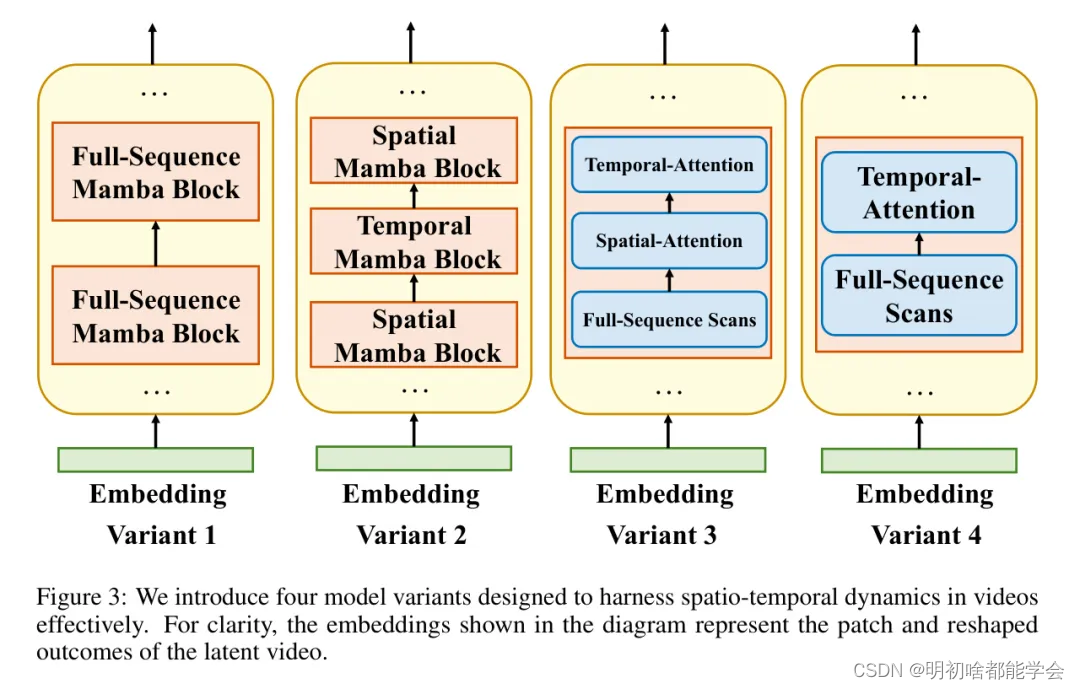
图2:原始的1D序列Mamba块和2D双向Mamba块。为了简化，省略了归一化和残差部分。
全局序列Mamba块。如图3(a)所示，这个变体指的是在这个时空输入的全序列中执行3DMamba扫描。继VideoMamba [51]之后，作者采用空间优先扫描用于作者的全局序列Mamba块。这种简单的操作已经被证明是高度有效的。它涉及根据空间标记的位置将它们排列，并逐帧地堆叠它们。作者将z Reshape为zu∈ R1×n.f T2趋N.wy×d作为全局序列
Mamba块的输入以捕捉空间优先信息。使用了双向Mamba层。空间和时间Mamba块交错。这种特定变体利用Mamba模块替代基于Transformer的视频生成扩散模型中的传统注意力模块，如[2;56; 57]的研究所指出的。如图3 (b)所示，这个变体的主体称为Matten，配备了两种类型的双向Mamba块:空间双向Mamba块和时序双向Mamba块。空间块旨在捕捉在相同时间索引下标记之间的空间细节，而时序块则负责在相同空间坐标下捕捉不同时间的信息。为了有效地处理空间信息，作者将z重构为z。∈R"f×5xd，这然后作为空间Mamba块的输入。
然后，作者将zReshape为zt ∈RS×nfXd，以供时序Mamba块处理时序信息。
全局序列玛巴块与时空注意力交错。尽管玛巴在长距离建模中展示了高效的性能，但与Transformer中的注意力操作相比，它在较短期序列建模中的优势并不明显[10]。因此，作者开发了一个混合块，如图3 ©所示，它利用了注意机制和玛巴的优势，对长短距离建模进行了整合。每个块由空间注意力计算、时间注意力计算和全局序列玛巴扫描ConCat组成。这种设计使作者的模型能够有效地捕捉视频潜在空间中的全局和局部信息。
全局序列玛巴块与时间注意力交错。

全局序列Mamba块中的扫描在空间域上是连续的，但在时间域上是断续的。因此，这个变体移除了空间注意力组件，同时保留了时间注意力块。因此，通过关注图3（d）所示的空间优先扫描增强时间注意力，作者努力提高模型在处理视频数据的动态方面的效率和精确性，从而确保在多样化的视频处理任务中具有鲁棒的性能。
Conditional Way of Timestep or Class
图3：作者引入了四种模型变体，旨在有效地利用视频中的时空动态。为了清晰起见，图中所示的嵌入表示潜在视频的Patch和Reshape结果。
借鉴Latte和DiS提出的框架，作者在两种不同的方法上进行了实验，将时间步或类别信息$c$嵌入到作者的模型中。第一种方法受到DiS的启发，将$c$视为标记，作者将这种策略称为_条件标记_。第二种方法采用了类似于自适应标准化(AdaN)的技术，专门为整合到Mamba块中而设计。这涉及到使用MLP层从$c$计算参数$y_c$和${\beta }_c$，形成操作
$$\text{AdaN}(f,c)=\text{cNorm}(f)+{\gamma }_c\cdot f，$$
其中$f$表示Mamba块中的特征图。此外，这种自适应标准化是在Mamba块的残差连接之前实现的，通过转换
$${\text{RC}}_s(f,c)=a\cdot f+\text{MambaScans}(\text{AdaN}(f,c))$$
来实现，其中MambaScans表示块内的双向Mamba扫描。作者将这种先进技术称为Mamba自适应标准化(M-AdaN)，它无缝地融入类别或时间步信息，以增强模型的响应性和上下文相关性。
Mamba and Attention Analysis
总之，作者提出的块的超参数包括隐藏大小$D$、扩展状态维度$E$和SSM维度$N$。Matten的所有设置在表2中详细列出，涵盖了不同的参数数量和计算成本，以彻底评估可扩展性性能。特别是，在生成$16\times 256\times 256$无条件视频时，采用了Patch大小$p=2$，分析了Gflop指标。与[10]一致，作者将所有模型的SSM维度$N$标准化为16。

Matten中的SSM块和Transformer架构中的自注意力机制对于有效的上下文建模都是不可或缺的。作者还提供了关于计算效率的详细理论分析。对于给定的序列$X\in {\mathbb{R}}^{1\times J\times D}$（标准设置$E=2$），自注意力（SA）、前馈网络（FFN）和SSM操作的计算复杂度分别计算如下:

$$\begin{array}{rl}O(SA)& =2\cdot J^2\cdot D,\\ O(FFN)& =4\cdot J\cdot D^2,\\ O(SSM)& =3\cdot J\cdot (2D)\cdot N+J\cdot (2D)\cdot N^2.\end{array}$$

其中，$O(SSM)$涉及与$B$、$C$和$D$的计算，而$J\cdot (2D)\cdot N^2$表示与$A$的计算。这表明自注意力的计算需求与序列长度$J$成二次方增长，而SSM操作则呈线性增长。值得注意的是，当$N$通常固定为16时，这种线性可扩展性使得Mamba架构特别适合处理像视频数据中全局关系建模这样的广泛序列。当比较$2\cdot J^2\cdot D$和$J\cdot (2D)\cdot N^2$这两个项时，很明显，Mamba块在计算效率上优于自注意力，特别是当序列长度$J$显著超过$N^2$时。对于关注空间和局部时间关系的较短期序列，当计算开销可以管理时，注意力机制提供了计算效率更高的选择，这一点得到了实证结果的支持。