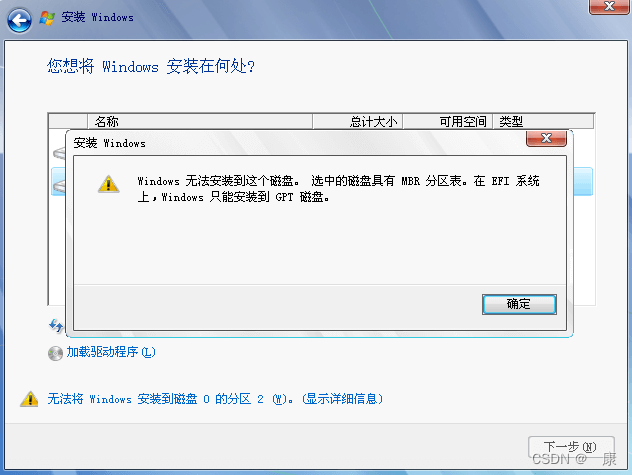
转换磁盘分区形式
步骤1. 先按照正常流程使用Windows系统安装光盘或系统U盘引导计算机。
步骤2. 在Windows安装程序中点击“开始安装”,然后按Shift+F10打开命令提示符。
步骤3. 依次输入以下命令,并在每一行命令后按一次Enter键执行。
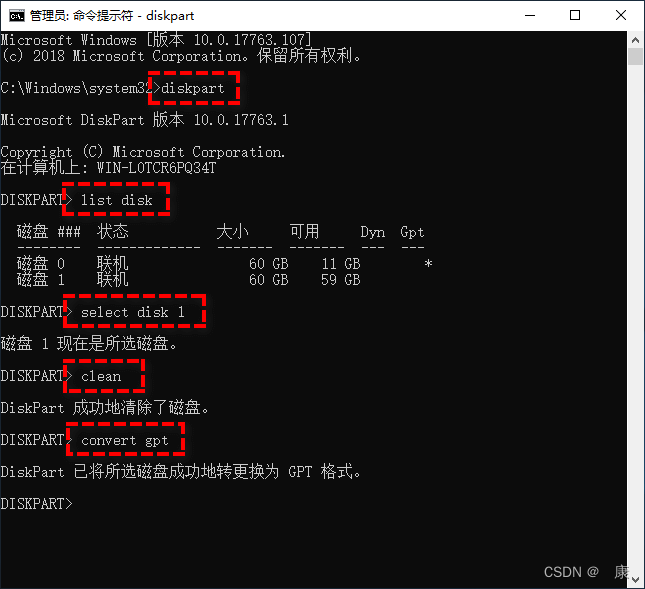
步骤4. 等待转换完成之后,退出命令提示符继续安装系统检查Windows无法安装的问题是否已被解决

步骤1. 先按照正常流程使用Windows系统安装光盘或系统U盘引导计算机。
步骤2. 在Windows安装程序中点击“开始安装”,然后按Shift+F10打开命令提示符。
步骤3. 依次输入以下命令,并在每一行命令后按一次Enter键执行。

步骤4. 等待转换完成之后,退出命令提示符继续安装系统检查Windows无法安装的问题是否已被解决
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1664056.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!