基于傅里叶变换的信号频域表示及能量频域分布揭示了信号在频域的特征，但傅里叶变换是一种整体变换，只能了解信号的全局特性，不能有效检测信号频率随时间的变化情况。只有把时域和频域结合起来才能更好地反映非平稳信号的特征。时频分析的基本思想是设计时间和频率的联合函数，同时描述信号在不同时间和频率的能量密度或强度。时频分析以联合时频分布的形式来表示信号的特性，克服了傅里叶分析时域和频域完全分离的缺陷，可以较准确地定位某一时刻出现哪些频率分量，以及某一频率分量分布在哪些时刻上。线性时频分析方法主要有：短时傅里叶变换、Gabor变换、小波变换、S 变换等。20世纪40年代Koenig提出了语谱图的方法。短时傅里叶变换由于实现简单已成为分析非平稳信号的有力工具。

STFT 的含义可解释为：在时域用窗函数去截信号h，假定h在窗函数的一个短时间间隔内是平稳的，对截下来的局部信号作傅里叶变换，即得到在t 时刻该段信号的傅里叶变换。不断地移动t，即不断地移动窗函数w的中心位置，可得到不同时刻的傅里叶变换。短时傅里叶变换实际上是一类加窗的傅里叶变换，用窗口函数w把信号划分成许多时间间隔，把每一时间间隔内的信号看作平稳信号，用傅里叶变换分析每一时间间隔，确定在不同时间间隔存在的频率，研究局部时间范围的频域特征。STFT 的优点是：物理意义明确，对整个信号采用单一分辨率进行研究，可以反映信号的整体时频趋势；由于其概念直接，算法简单，实现容易，已经成为研究非平稳信号十分有力的工具，在许多领域（如时变滤波、提高分辨率、地震旋回分析和瞬时属性提取等）得到广泛的应用。

基于此，提出一种基于短时傅里叶变换域的一维信号邻域降噪方法，该方法使用最小控制递归平均方法估计噪声水平，并在STFT域使用Stein无偏风险估计降噪，部分代码如下：

function STFTcoef = STFT(f, time_win, factor_redund, f_sampling)
%
% 1D Windowed Fourier Transform. 
%
% Input:
% - f: Input 1D signal.
% - time_win: window size in time (in millisecond).
% - factor_redund: logarithmic redundancy factor. The actual redundancy
%   factor is 2^factor_redund. When factor_redund=1, it is the minimum
%   twice redundancy. 
% - f_sampling: the signal sampling frequency in Hz.
%
% Output:
% - STFTcoef: Spectrogram. Column: frequency axis from -pi to pi. Row: time
%   axis. 
%


% Check that f is 1D
if length(size(f)) ~= 2 | (size(f,1)~=1 && size(f,2)~=1)
    error('The input signal must 1D.');
end

if size(f,2) == 1
    f = f';
end

% Window size
size_win = round(time_win/1000 * f_sampling);

% Odd size for MakeHanning
if mod(size_win, 2) == 0
    size_win = size_win + 1;
end
halfsize_win =  (size_win - 1) / 2;

w_hanning = MakeHanning(size_win); 

Nb_win = floor(length(f) / size_win * 2);

% STFTcoef = zeros(2^(factor_redund-1), size_win, Nb_win-1);
STFTcoef = zeros(size_win, (2^(factor_redund-1) * Nb_win-1));

shift_k = round(halfsize_win / 2^(factor_redund-1));
% Loop over 
for k = 1 : 2^(factor_redund-1)    
    % Loop over windows
    for j = 1 : Nb_win - 2 % Ingore the last few coefficients that do not make a window
        f_win = f(shift_k*(k-1)+(j-1)*halfsize_win+1 : shift_k*(k-1)+(j-1)*halfsize_win+size_win);
        STFTcoef(:, (k-1)+2^(factor_redund-1)*j) = fft(f_win .* w_hanning');
    end
end
%完整代码可由知乎学术咨询获得https://www.zhihu.com/consult/people/792359672131756032

出图如下：

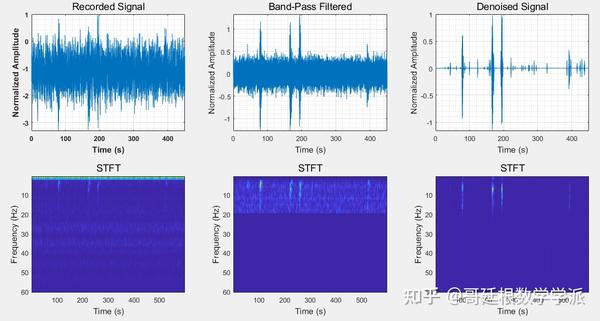
完整代码可由知乎学术咨询获得：

工学博士，担任《Mechanical System and Signal Processing》《中国电机工程学报》等期刊审稿专家，擅长领域：现代信号处理，机器学习/深度学习，时间序列分析/预测，电气设备（电机，变压器等）表面缺陷检测、电气设备（电机，变压器等）异常检测、电气设备（电机，变压器等）故障诊断与健康管理PHM、电气设备（电机，变压器等）剩余使用寿命预测等。