文献中出现了许多交流变换器建模技术,包括电流注入法、电路平均法和状态空间平均法。尽管给定方法的支持者可能更喜欢用特定形式表示最终结果,但几乎所有方法的最终结果都是等效的。所有人都会赞同,平均和小信号线性化是PWM变换器建模的关键步骤。
动态系统的状态空间描述是现代控制理论的支柱;状态空间平均法利用这一描述导出了PWM开关变换器的小信号平均方程。状态空间平均过程的一个好处是其结果的通用性:只要能写出原变换器的状态方程,总能得到一个小信号平均模型。
1.网络的状态方程
状态空间描述是描述系统的微分方程的正则形式。对于线性网络,状态变量的导数表示为系统独立输入和状态变量本身的线性组合。系统的物理状态变量通常与能量存储有关,对于典型的变换器电路,物理状态变量是独立的电感电流和电容电压。其他典型的状态变量包括电机轴的位置和速度。在给定的时间点上,状态变量的值取决于系统以前的历史,而不是取决于系统输入的当前值。要解系统的微分方程,必须指定状态变量的初值。如果知道系统的状态,也就是所有状态变量在给定时间t0的值,如果还知道系统的输入,那么原则上就可以解出系统的状态方程来找到未来任何时间的系统波形。
系统的状态方程可以写成紧矩阵形式:
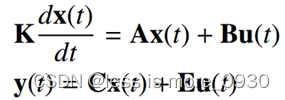
其中,状态矢量x(t)是包含所有状态变量,即电感电流、电容电压等的矢量。输入矢量u(t)包含系统所有的独立输入,如输入电压源vg(t)。状态矢量的导数是一个矢量,它的元素等于状态矢量对应元素的导数。

在状态方程紧矩阵形式的标准形式中,K是包含电容、电感和互感(如果有)值的矩阵,使得Kdx(t)/dt是包含电感绕组电压和电容电流的矢量。在其他物理系统中,K可能包含其他量,如转动惯量或质量。状态方程紧矩阵形式表达式说明系统的电感电压和电容电流可以表示成状态变量和独立输入量的线性组合。矩阵A和B包含比例常数。
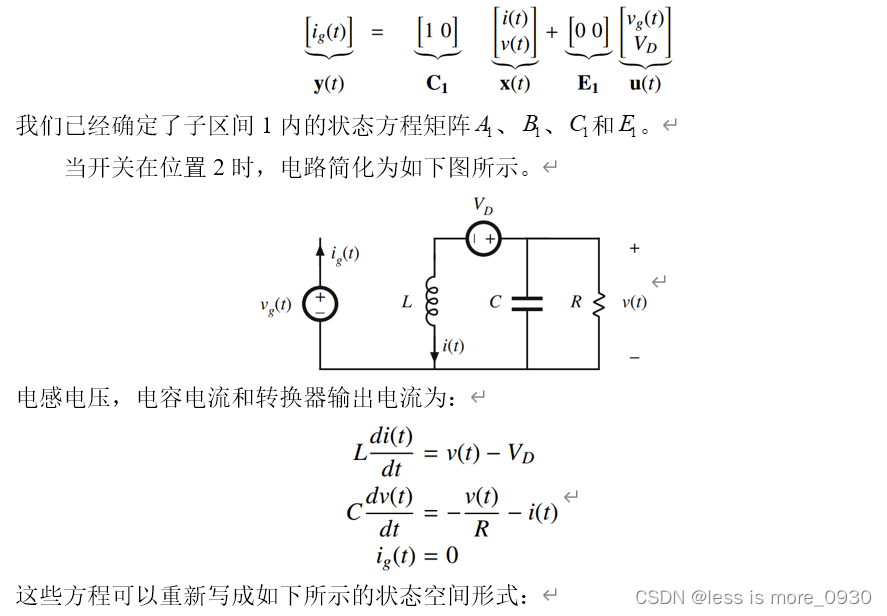
也可能需要计算与状态向量x(t)或输入向量u(t)的元素不一致的其他电路波形。一般来说,这些其他信号是相关的波形,可以表示为状态向量和输入向量元素的线性组合。向量y(t)通常叫做输出向量。我们可以自由地在这个向量中放置任何相关的信号,而不管这个信号实际上是否是一个物理输出。转换器输入电流ig(t)通常被选为y(t)的一个元素。在状态方程中,向量y(t)的元素被表示成向量x(t)和u(t)的线性组合。矩阵C和E包含比例常数。
举个例子,写出下图所示电路的状态方程。
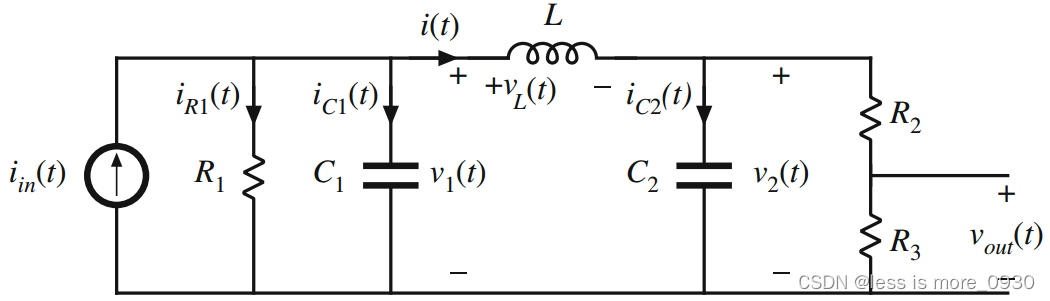
该电路包含两个电容和一个电感,因此物理状态变量是独立电容电压v1(t)和v2(t),以及电感电流i(t)。因此可以定义状态矢量为:

因为此处没有耦合电感,矩阵K是对角阵,只包含电容值和电感值:

电路有一个独立输入,即电流源iin(t)。因此,我们需要定义输入矢量:
![]()
我们可以自由地将任何相关信号放入向量y(t)中。假设我们还想计算电压vout(t)和电流iR1(t)。因此可以定义y(t)为:
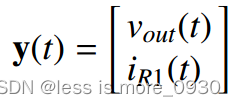
为了写出正则形式的状态方程,我们需要用状态矢量x(t)和输入矢量u(t)的线性组合来表示电感电压和电容电流,即用v1(t)、v2(t)、i(t)和iin(t)的线性组合来表示。
电容电流iC1(t)由节点方程得到:

这个方程将成为紧矩阵形式状态空间方程的第一行。电容电流iC2(t)由节点方程得到:

注意,我们已经仔细的将这个电流表示为仅由x(t)和u(t)元素组成的线性组合。
由回路方程可得电感电压为:

将上述两个电容电流和电感电压汇总成矩阵形式,可得:
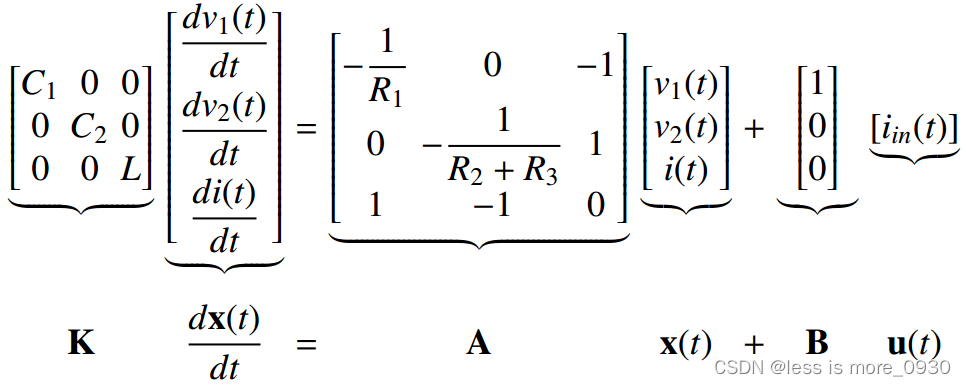
现在矩阵A和B已知。
也有必要将y(t)的元素表示为x(t)和u(t)元素的线性组合。通过求解如下图所示的电路。

可以将输出电压vout(t)用v2(t)这一项表示出来:

同样,iR1(t)可以用v1(t)表示为:
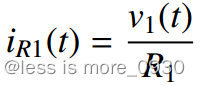
将vout(t)和iR1(t)的表达式代入紧矩阵形式状态空间方程可得:

如上式所示,现在就得到了矩阵C和E。
2.基础状态方程平均模型
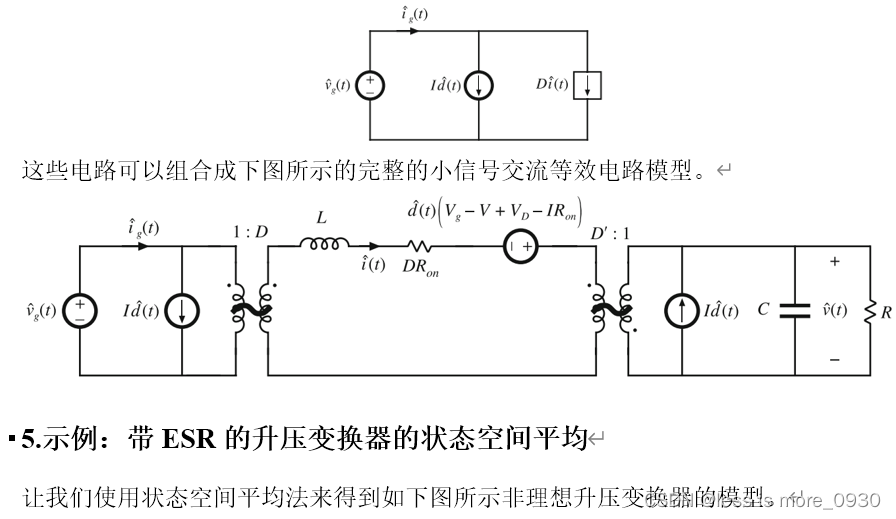
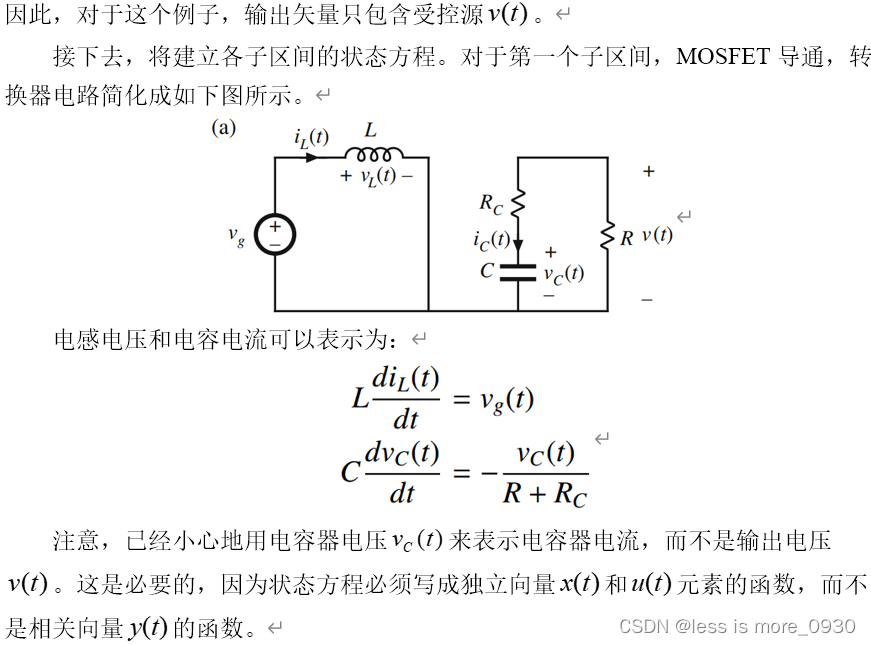
假设现在给定一个工作在CCM下的PWM转换器。转换器电路包含形成状态向量x(t)的独立状态,并且变换器由形成输入向量u(t)的独立源驱动。在第一个子区间内,当开关在位置1时,转换器简化成可以用下式描述的线性电路:
























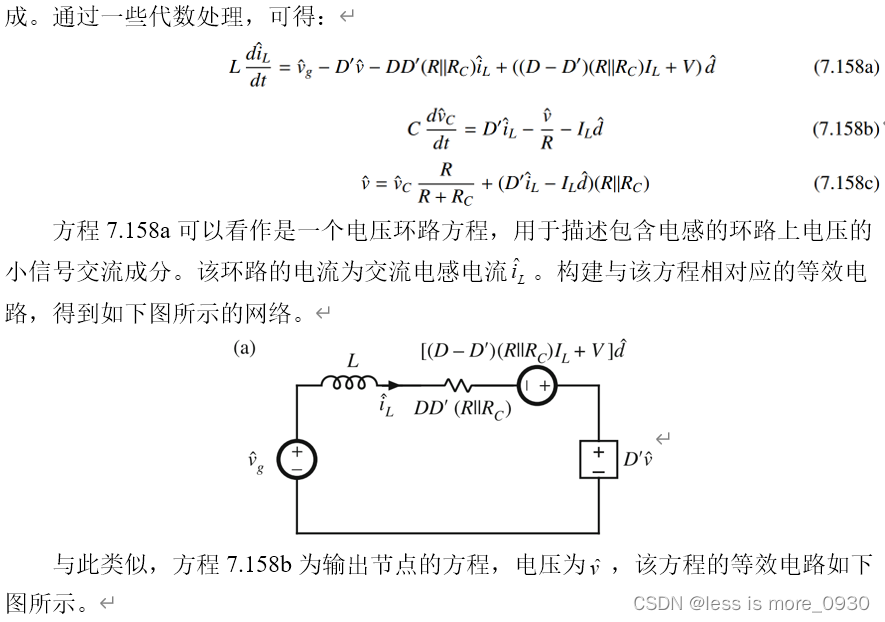
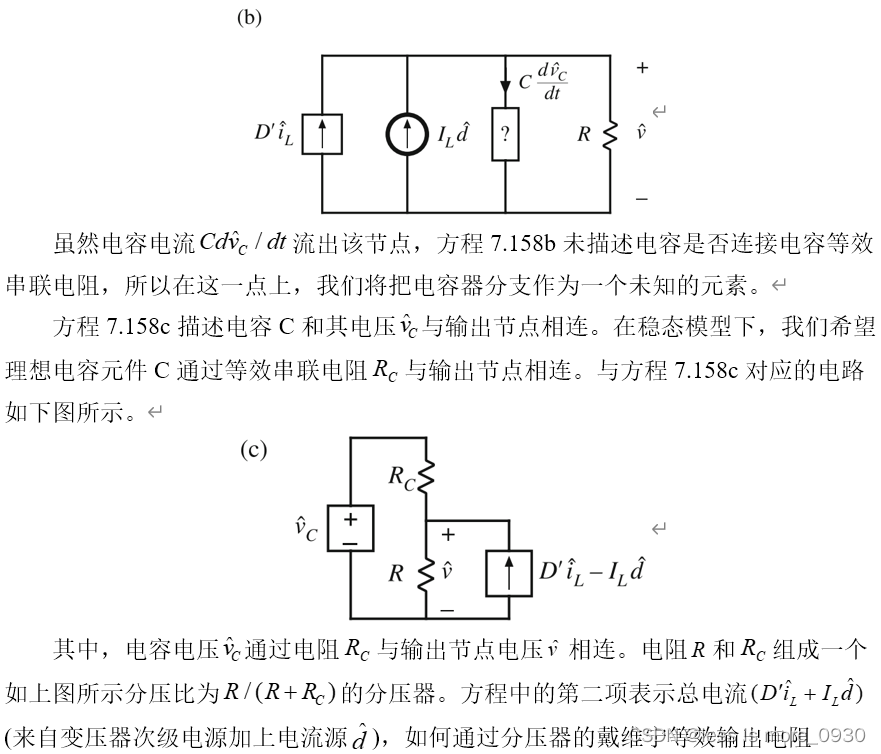
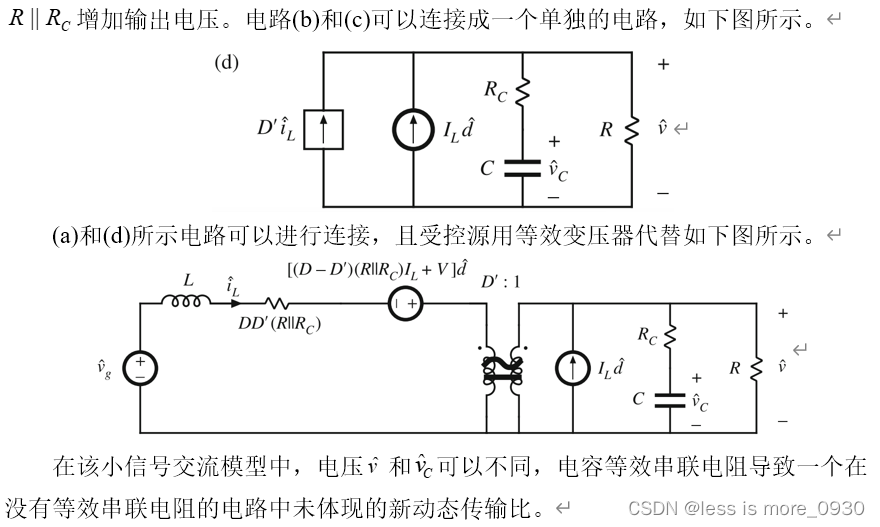
6.总结
(1)CCM变换器分析技术可以扩展到预测变换器的交流行为。关键步骤是在一个开关周期内平均转换器波形。这消除了开关谐波,从而直接暴露了波形所需的直流和低频交流分量。特别是,通常会找到平均电感电压、电容电流和变换器输入电流的表达式。
(2)由于开关变换器是非线性系统,因此需要建立小信号线性化模型。该过程通过对静止工作点的平均模型进行扰动和线性化来实现。
(3)可以构造直流等效电路的相同方法构造交流等效电路。如果需要,可以对交流等效电路进行改进,以考虑转换器损耗和其他非理想性的影响。
(4)传统脉宽调制器电路具有线性增益,依赖于锯齿波的斜率,或等价于零。
由于开关变换器是非线性系统,因此需要建立小信号线性化模型。这是通过对静止工作点的平均模型进行扰动和线性化来实现的。
(5)正则电路描述了所有工作在连续导通模式下的直流-直流PWM变换器共有的基本特性。该模型的核心是理想的1:M(D)变压器,以表示基本的dc-dc传递函数,并在这里推广到包括交流变化。变换器无功元件在网络中引入了一个有效的低通滤波器。该模型还包括代表占空比变化影响的独立源。为方便参考,将几种基本转换器正则模型中的参数值制成表格。
(6)状态空间平均方法本质上与第7.2节的基本方法相同,只是使用了状态空间网络描述的形式。一般结果列在第7.5.2节中。状态空间平均是一种形式的方法,它展示了如何总是可以推导出小信号平均模型,只要可以为每个子区间写出状态方程。




![[附源码+视频教程]暗黑纪元H5手游_架设搭建_畅玩三网全通西方3D世界_带GM](https://img-blog.csdnimg.cn/img_convert/bb80720776c56835002eb4f324794567.webp?x-oss-process=image/format,png)