TOPK问题

TOP-K问题：即求数据结合中前K个最大的元素或者最小的元素，一般情况下数据量都比较大。

比如：专业前10名、世界500强、富豪榜、游戏中前100的活跃玩家等。

情况1——数据量小

对于Top-K问题，能想到的最简单直接的方式就是排序，

就是我们建N个数的大堆，再Pop K次就行了

 代码展示（最大的K个）

#include<stdio.h>
#include<assert.h>
#include<stdlib.h>
#include<stdbool.h>
#include<string.h>
typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;
void Swap(HPDataType* p1, HPDataType* p2)
{
	HPDataType x = *p1;
	*p1 = *p2;
	*p2 = x;
}

//堆的向下调整（大堆）  
void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1; // 计算左子节点的索引  

	// 当 child 索引在数组范围内时执行循环  
	while (child < n)
	{
		// 如果右子节点存在且大于左子节点  
		if (child + 1 < n && a[child + 1] > a[child])
		{
			++child; // 更新 child 为右子节点的索引  
		}

		// 如果 child 节点（现在是左右子节点中较大的一个）大于 parent 节点  
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]); // 交换 parent 和 child 的值  
			parent = child; // 更新 parent 为刚刚交换过的 child 的索引  
			child = parent * 2 + 1; // 重新计算左子节点的索引  
		}
		else
		{
			break; // child 节点不大于 parent 节点，无需继续调整，退出循环  
		}
	}
}

void HeapInit(HP* php)
{
	assert(php);

	php->a = (HPDataType*)malloc(sizeof(HPDataType) * 4);
	if (php->a == NULL)
	{
		perror("malloc fail");
		return;
	}

	php->size = 0;
	php->capacity = 4;
}

bool HeapEmpty(HP* php)
{
	assert(php);
	return php->size == 0;
}
void HeapDestroy(HP* php)
{
	assert(php);

	free(php->a);
	php->a = NULL;
	php->capacity = php->size = 0;
}




// 除了child这个位置，前面数据构成堆
void AdjustUp(HPDataType* a, int child)
{
	int parent = (child - 1) / 2;
	//while (parent >= 0)
	while (child > 0)
	{
		if (a[child] > a[parent])
		{
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else
		{
			break;
		}
	}
}



void HeapPush(HP* php, HPDataType x)
{
	assert(php);

	if (php->size == php->capacity)
	{
		HPDataType* tmp = (HPDataType*)realloc(php->a, sizeof(HPDataType) * php->capacity * 2);
		if (tmp == NULL)
		{
			perror("realloc fail");
			return;
		}
		php->a = tmp;
		php->capacity *= 2;
	}

	php->a[php->size] = x;
	php->size++;

	AdjustUp(php->a, php->size - 1);
}

//打印堆
void HeapPrint(HP* php)
{
	assert(php);
	//按照物理结构进行打印
	int i = 0;
	for (i = 0; i < php->size; i++)
	{
		printf("%d ", php->a[i]);
	}
	printf("\n");
}

void HeapPop(HP* php)
{
	assert(php);
	assert(!HeapEmpty(php));

	// 删除数据
	Swap(&php->a[0], &php->a[php->size - 1]);
	php->size--;

	AdjustDown(php->a, php->size, 0);
}

HPDataType HeapTop(HP* php)
{
	assert(php);
	return php->a[0];
}



int HeapSize(HP* php)
{
	assert(php);
	return php->size;
}


int main()
{
	HP hp;
	HeapInit(&hp);
	HeapPush(&hp, 4);
	HeapPush(&hp, 180);
	HeapPush(&hp, 42);
	HeapPush(&hp, 12);
	HeapPush(&hp, 21);
	HeapPush(&hp, 3);
	HeapPush(&hp, 1);
	HeapPush(&hp, 2);
	HeapPush(&hp, 50);
	HeapPush(&hp, 5);
	HeapPush(&hp, 5);
	HeapPush(&hp, 150);
	HeapPush(&hp, 5);
	HeapPush(&hp, 45);
	HeapPush(&hp, 5);

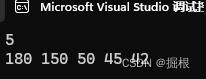
	int k = 0;
	scanf("%d", &k);
	while (!HeapEmpty(&hp) && k--)
	{
		printf("%d ", HeapTop(&hp));
		HeapPop(&hp);
	}
	printf("\n");

	return 0;
}

情况2——数据量大 

但是：如果数据量非常大，排序就不太可取了(可能 数据都不能一下子全部加载到内存中)。

最佳的方式就是用堆来解决，基本思路如下：

1. 用数据集合中前K个元素来建堆

• 前k个最大的元素，则建小堆
• 前k个最小的元素，则建大堆

有人就好奇了，为什么找最大的要建小堆而不是大堆，原因很简单，

建小堆，最大的K个元素肯定可以进去，但是如果建的是大堆的话，假设前K个里就遇到了最大的，它就会阻止后面其他次大的元素进去堆

2. 用剩余的N-K个元素依次与堆顶元素来比较，不满足则替换堆顶元素

将剩余N-K个元素依次与堆顶元素比，如果这个数据比堆顶的数据大，就替代它进堆，遍历完后堆中剩余的K个元素就是所求的前K个最小或者最大的元素。

代码展示

代码分两步执行

我们先来看看源码

#include<stdio.h>
#include<time.h>
#include<stdlib.h>
#include<assert.h>

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}HP;
void Swap(HPDataType* p1, HPDataType* p2)
{
	HPDataType x = *p1;
	*p1 = *p2;
	*p2 = x;
}

//堆的向下调整（小堆）—— 左右子树都是小堆
void AdjustDown(HPDataType* a, int n, int parent)
{
	int child = parent * 2 + 1;
	while (child < n)
	{
		// 选出左右孩子中大的那一个
		if (child + 1 < n && a[child + 1] < a[child])
		{
			++child;
		}

		if (a[child] < a[parent])
		{
			Swap(&a[child], &a[parent]);
			parent = child;
			child = parent * 2 + 1;
		}
		else
		{
			break;
		}
	}
}

void PrintTopK(const char* file, int k)
{
	// 1. 建堆--用a中前k个元素建小堆
	int* topk = (int*)malloc(sizeof(int) * k);
	assert(topk);

	FILE* fout = fopen(file, "r");
	if (fout == NULL)
	{
		perror("fopen error");
		return;
	}

	// 读出前k个数据建小堆
	for (int i = 0; i < k; ++i)
	{
		fscanf(fout, "%d", &topk[i]);
	}

	for (int i = (k - 2) / 2; i >= 0; --i)
	{
		AdjustDown(topk, k, i);
	}

	// 2. 将剩余n-k个元素依次与堆顶元素交换，不满则则替换
	int val = 0;
	int ret = fscanf(fout, "%d", &val);
	while (ret != EOF)
	{
		if (val > topk[0])
		{
			topk[0] = val;
			AdjustDown(topk, k, 0);
		}

		ret = fscanf(fout, "%d", &val);
	}

	for (int i = 0; i < k; i++)
	{
		printf("%d ", topk[i]);
	}
	printf("\n");

	free(topk);
	fclose(fout);
}

void CreateNDate()
{
	// 造数据
	int n = 10000000;
	srand(time(0));
	const char* file = "data.txt";
	FILE* fin = fopen(file, "w");
	if (fin == NULL)
	{
		perror("fopen error");
		return;
	}

	for (size_t i = 0; i < n; ++i)
	{
		int x = rand() % 10000;
		fprintf(fin, "%d\n", x);
	}

	fclose(fin);
}

第一步创建数据 

int main()
{
	CreateNDate();
	return 0;
}

我们先运行一下上面的代码，然后就能在目录下看到我们创建了一个txt文件 

这里就有我们要的超大量数据，我们可以把它添到目录下来，方便修改

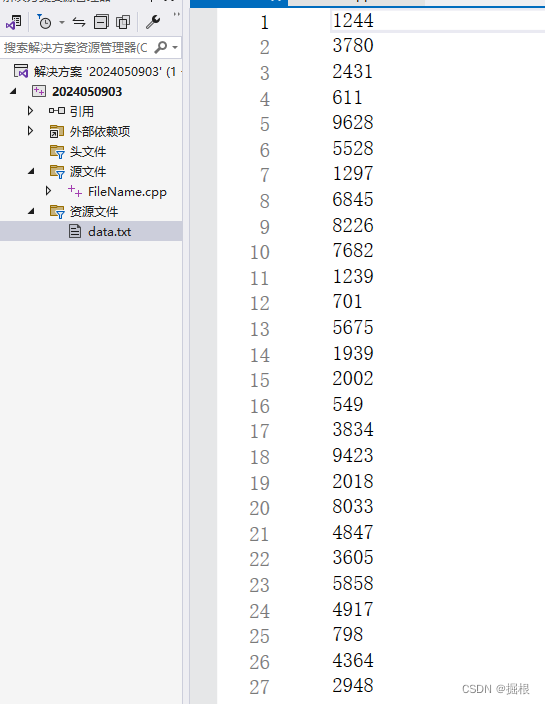
我们创建的都是10000以内的数据，

第二步——修改数据 

int main()
{
	PrintTopK("data.txt",10);
	return 0;
}

我们先运行一下

确认都在10000内之后，就去修改数据

再运行上面的代码，得到下面结果 

 我们发现，修改后的7个数据全在里面，也就说明我们的代码没有问题