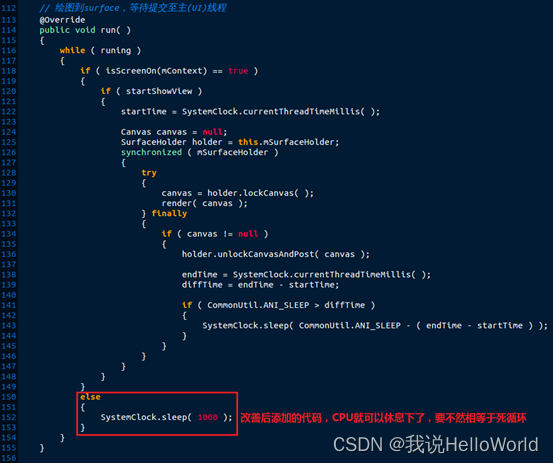
要逐步推导多变量线性回归的梯度计算过程,我们首先需要明确模型和损失函数的形式,然后逐步求解每个参数的偏导数。这是梯度下降算法核心部分,因为这些偏导数将指导我们如何更新每个参数以最小化损失函数。
模型和损失函数
考虑一个多变量线性回归模型,模型预测可以表示为:
h
θ
(
x
)
=
θ
0
+
θ
1
x
1
+
θ
2
x
2
+
⋯
+
θ
n
x
n
h_{\theta}(x) = \theta_0 + \theta_1 x_1 + \theta_2 x_2 + \dots + \theta_n x_n
hθ(x)=θ0+θ1x1+θ2x2+⋯+θnxn
其中
x
=
[
x
1
,
x
2
,
…
,
x
n
]
x = [x_1, x_2, \dots, x_n]
x=[x1,x2,…,xn] 是输入特征,
θ
=
[
θ
0
,
θ
1
,
…
,
θ
n
]
\theta = [\theta_0, \theta_1, \dots, \theta_n]
θ=[θ0,θ1,…,θn] 是模型参数。
我们使用均方误差作为损失函数,对于所有训练数据:
J
(
θ
)
=
1
2
m
∑
i
=
1
m
(
h
θ
(
x
(
i
)
)
−
y
(
i
)
)
2
J(\theta) = \frac{1}{2m} \sum_{i=1}^m \left( h_{\theta}(x^{(i)}) - y^{(i)} \right)^2
J(θ)=2m1i=1∑m(hθ(x(i))−y(i))2
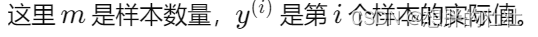
计算梯度
为了使用梯度下降算法,我们需要计算损失函数 J ( θ ) J(\theta) J(θ) 关于每个参数 θ j \theta_j θj 的偏导数。假设 j 代表特定的参数索引,包括 0,即截距项 θ 0 \theta_0 θ0:
-
扩展损失函数:
J ( θ ) = 1 2 m ∑ i = 1 m ( θ 0 + θ 1 x 1 ( i ) + ⋯ + θ n x n ( i ) − y ( i ) ) 2 J(\theta) = \frac{1}{2m} \sum_{i=1}^m \left( \theta_0 + \theta_1 x_1^{(i)} + \dots + \theta_n x_n^{(i)} - y^{(i)} \right)^2 J(θ)=2m1i=1∑m(θ0+θ1x1(i)+⋯+θnxn(i)−y(i))2 -
对 ( \theta_j ) 求偏导数:
为了求 ∂ J ∂ θ j \frac{\partial J}{\partial \theta_j} ∂θj∂J我们需要应用链式法则:
∂ J ∂ θ j = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) ∂ ∂ θ j ( h θ ( x ( i ) ) ) \frac{\partial J}{\partial \theta_j} = \frac{1}{m} \sum_{i=1}^m \left( h_{\theta}(x^{(i)}) - y^{(i)} \right) \frac{\partial}{\partial \theta_j} \left( h_{\theta}(x^{(i)}) \right) ∂θj∂J=m1i=1∑m(hθ(x(i))−y(i))∂θj∂(hθ(x(i))) -
推导 ∂ ∂ θ j h θ ( x ( i ) ) \frac{\partial}{\partial \theta_j} h_{\theta}(x^{(i)}) ∂θj∂hθ(x(i))
因为 h θ ( x ( i ) ) = θ 0 + θ 1 x 1 ( i ) + ⋯ + θ n x n ( i ) h_{\theta}(x^{(i)}) = \theta_0 + \theta_1 x_1^{(i)} + \dots + \theta_n x_n^{(i)} hθ(x(i))=θ0+θ1x1(i)+⋯+θnxn(i)所以
∂ ∂ θ j h θ ( x ( i ) ) = x j ( i ) \frac{\partial}{\partial \theta_j} h_{\theta}(x^{(i)}) = x_j^{(i)} ∂θj∂hθ(x(i))=xj(i)
这里 x j ( i ) x_j^{(i)} xj(i) 是第 i 个样本的第 j 个特征。 -
将导数放回梯度公式:
∂ J ∂ θ j = 1 m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \frac{\partial J}{\partial \theta_j} = \frac{1}{m} \sum_{i=1}^m \left( h_{\theta}(x^{(i)}) - y^{(i)} \right) x_j^{(i)} ∂θj∂J=m1i=1∑m(hθ(x(i))−y(i))xj(i)
参数更新规则
在梯度下降算法中,使用上面计算的梯度来更新每个参数:
θ
j
:
=
θ
j
−
α
∂
J
∂
θ
j
\theta_j := \theta_j - \alpha \frac{\partial J}{\partial \theta_j}
θj:=θj−α∂θj∂J
这里的 α 是学习率,控制参数更新的步长。
通过这个过程,每一次迭代更新参数,直到算法收敛(即梯度接近零或者达到预设的迭代次数)。
这就是多变量梯度下降中梯度的计算过程,它使我们能够有效地最小化损失函数,并逐步
优化模型参数。







![[附源码+视频教程]暗黑纪元H5手游_架设搭建_畅玩三网全通西方3D世界_带GM](https://img-blog.csdnimg.cn/img_convert/bb80720776c56835002eb4f324794567.webp?x-oss-process=image/format,png)