目录
问题描述:
实现代码与解析:
递归:
原理思路:
含有内存释放版:
问题描述:
给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
一般来说,删除节点可分为两个步骤:
- 首先找到需要删除的节点;
- 如果找到了,删除它。
示例 1:
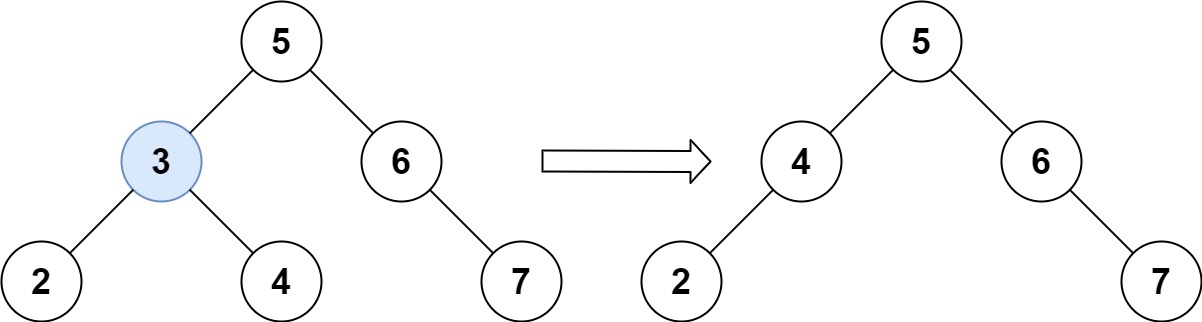
输入:root = [5,3,6,2,4,null,7], key = 3 输出:[5,4,6,2,null,null,7] 解释:给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。 一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。 另一个正确答案是 [5,2,6,null,4,null,7]。
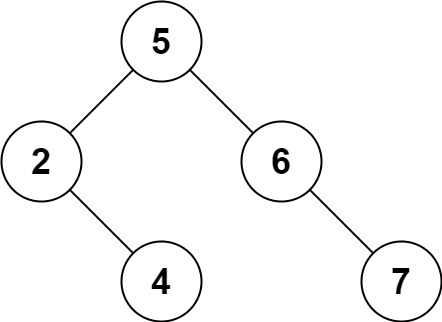
示例 2:
输入: root = [5,3,6,2,4,null,7], key = 0 输出: [5,3,6,2,4,null,7] 解释: 二叉树不包含值为 0 的节点
示例 3:
输入: root = [], key = 0 输出: []
实现代码与解析:
递归:
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key)
{ //未找到key
if(root==NULL) return NULL;
//找到了key结点
if(root->val==key)
{
//为叶子结点,左右子树为空
if(root->left==NULL&&root->right==NULL) return NULL;
//左子树为空,右子树不空
else if(root->left==NULL&&root->right!=NULL) return root->right;
//左子树不空,右子树为空
else if(root->left!=NULL&&root->right==NULL) return root->left;
//左右子树都不空
else
{
TreeNode* cur=root->right;
while(cur->left)
{
cur=cur->left;
}
cur->left=root->left;//连接
root=root->right;//更新新的根结点
return root;
}
}
//递归
if (root->val > key) root->left = deleteNode(root->left, key);
if (root->val < key) root->right = deleteNode(root->right, key);
return root;
}
};原理思路:
这题的重点就在于把所有的删除情况都考虑到。有以下几种情况:
一、未找到删除结点,之间返回NULL。
二、找到了删除结点。1、左右子树都为空,为叶子结点,删除结点,返回根节点NULL。
2、左子树为空,右子树不为空,删除结点,返回右子树为根节点。
3、左子树不为空,右子树为空,删除结点,返回左子树为根结点。
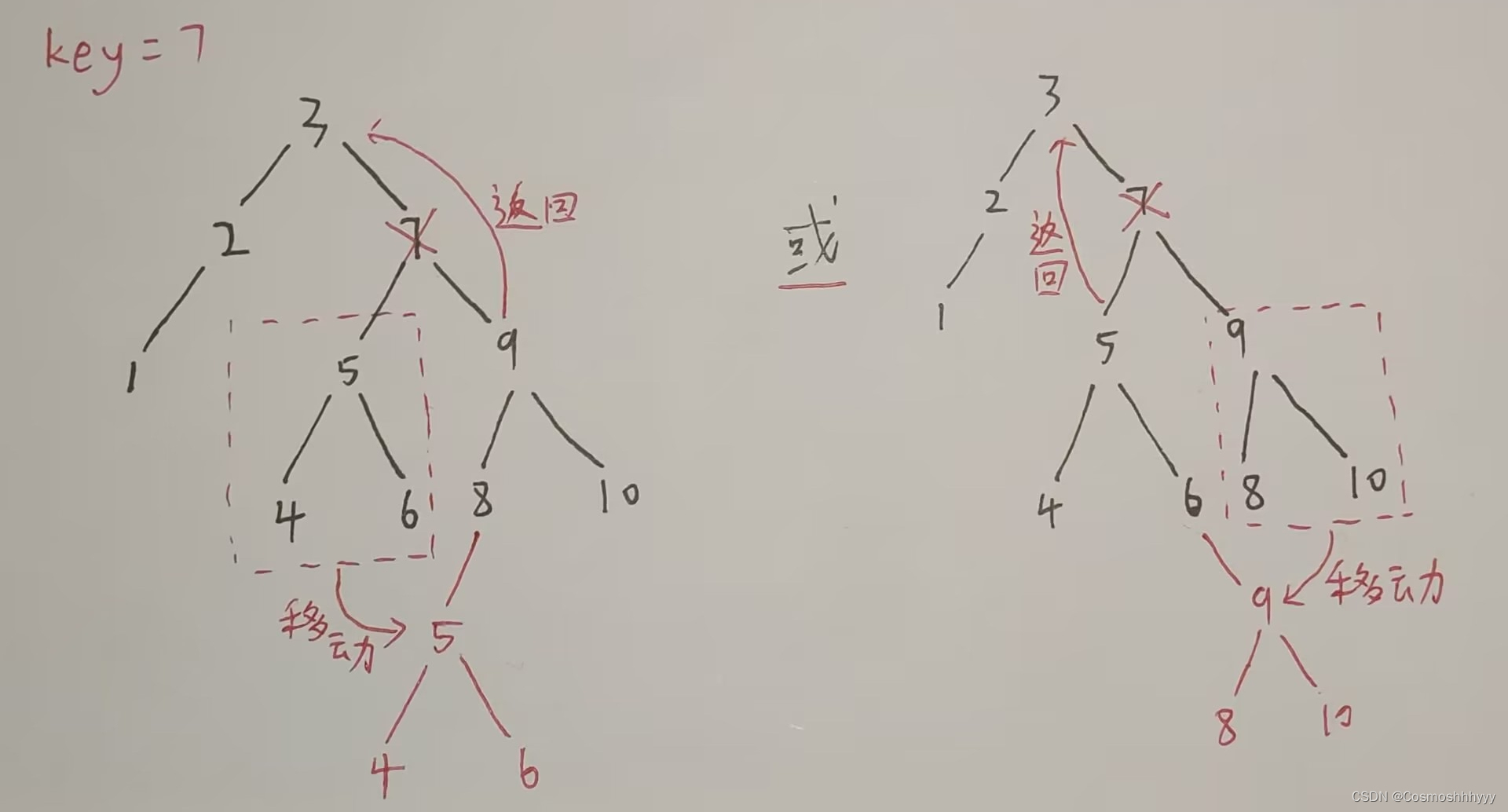
4、左右子树都不为空,我们将左子树移动到右子树结点中仅次于根节点的值的结点的左子树上,删除结点,返回右子树为根节点,或则将右子树移动到左子树中仅大于根节点值的结点的右子树上,删除结点,返回左子树为根结点。这里我们用的前一种。
可能还会有很多人不理解最后一种情况,我图画出来,大家可以着看,如下:
上面的代码我们为了整洁,其实只改变了指针的指向,并没有释放内存。下面给出释放内存的代码。
含有内存释放版:
class Solution {
public:
TreeNode* deleteNode(TreeNode* root, int key)
{ //未找到key
if(root==NULL) return NULL;
//找到了key结点
if(root->val==key)
{
//为叶子结点,左右子树为空
if(root->left==NULL&&root->right==NULL)
{
delete root;
return NULL;
}
//左子树为空,右子树不空
else if(root->left==NULL&&root->right!=NULL)
{
TreeNode* temp=root->right;
delete root;
return temp;
}
//左子树不空,右子树为空
else if(root->left!=NULL&&root->right==NULL)
{
TreeNode* temp=root->left;
delete root;
return temp;
}
//左右子树都不空
else
{
TreeNode* cur=root->right;
while(cur->left)
{
cur=cur->left;
}
cur->left=root->left;//连接
TreeNode* temp=root->right;
delete root;
return temp;
}
}
//递归
if (root->val > key) root->left = deleteNode(root->left, key);
if (root->val < key) root->right = deleteNode(root->right, key);
return root;
}
};