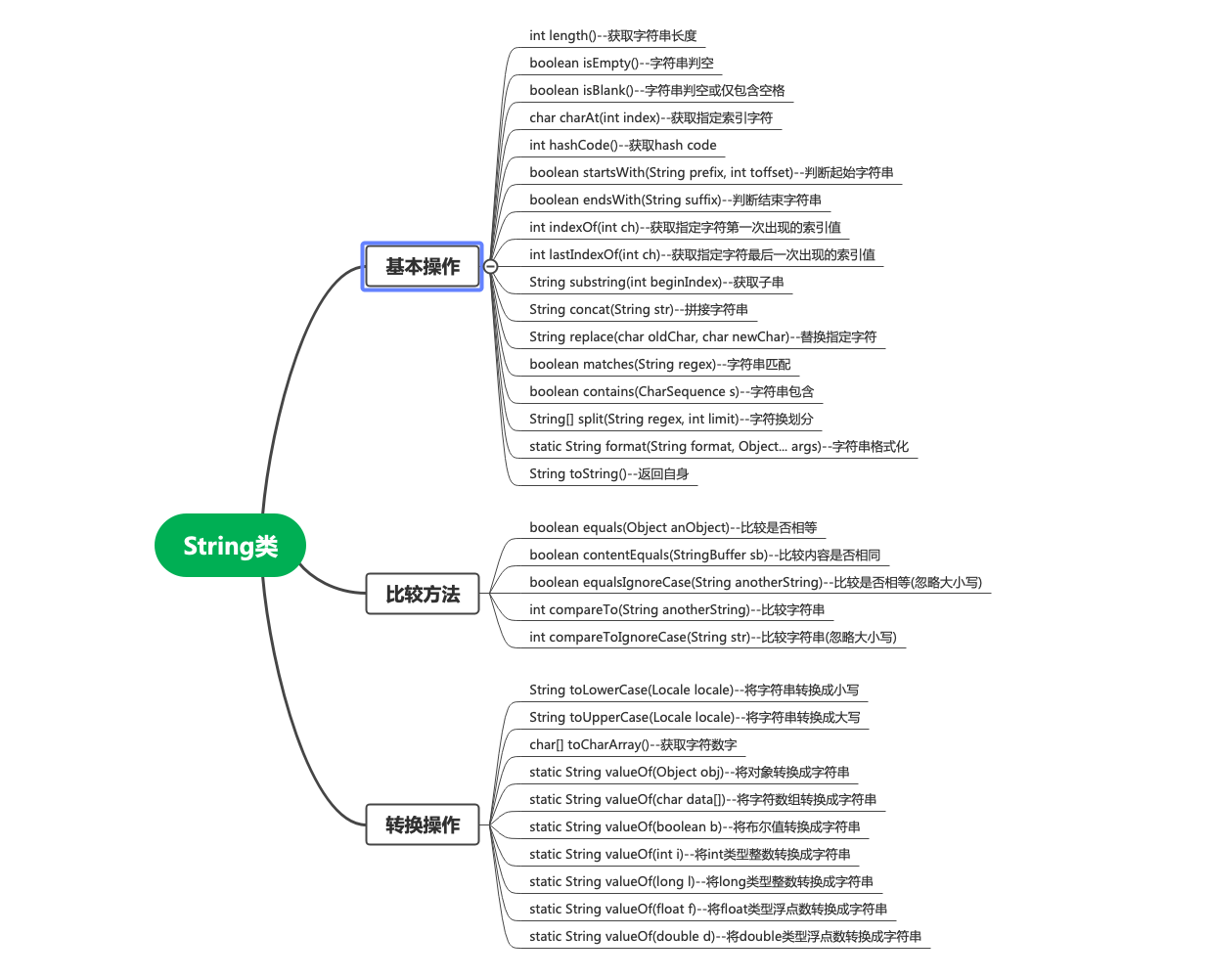
文献阅读：Towards Out-of-Distribution Sequential Event Prediction：A Causal Treatment

文献阅读：Towards Out-of-Distribution Sequential Event Prediction：A Causal Treatment
- 1. 问题描述
- 2. 方法 & 模型设计
  - 1. loss定义
  - 2. 模型设计
- 3. 实验 & 结果
  - 1. 基础实验
  - 2. CaseQ策略细节分析
- 4. 结论 & 总结

文献链接：https://arxiv.org/abs/2210.13005

1. 问题描述

这篇文章是我最近刷到的一篇工作，和我最近的工作有一点相似，所以就想拿来参考一下。

这篇文章针对的主要训练数据与线上服务的数据偏差问题。

具体而言，当前推荐模型的训练模型往往都是采用历史某一个时间段内的真实点击数据拟合用户与商品之间的关联性，从而预测未来某个时刻用户对于某一个商品的感兴趣程度，并用ctr或者cvr进行表征。

但是这样一来会带来一定的问题：

历史训练数据所处的时间段与线上服务的时间存在一定的gap，导致商品的分布与线上服务当中真实的商品数据分布存在一定的偏差，劣化模型的效果，且这种劣化作用会随着时间的增长而增大。

举例来说，如果用户上次浏览点击的时候是夏季，看了几件T恤，然后半年过去了，他在冬季重新浏览了一下，这个时候他更可能买羽绒服，而不会是T恤，虽然显然后者与用户的浏览历史关联度更高。更极端的，一个用户如果在08年的时候浏览过手机，那可能他点了一堆诺基亚，而到了22年，苹果华为早已是主流了，诺基亚可能都已经不存在这个商品类目了。

因此，这篇文章就尝试搞定上述问题，他们的方法也比较直观，就是在事件（商品点击）当中引入事件发生时的context信息，从而使得上述这种随时间增加而产生的商品分布偏差可以尽可能地被抹除。

2. 方法 & 模型设计

如前所述，这篇文章的核心方法就是在事件的预测当中引入context信息。

但是这里也存在一定的问题，主要就是隐私保护的问题，使得事实上现在我们基本都不太能够获取到用户点击发生时的context信息。

而文中针对这个问题的处理文中使用的方法也是相对来说比较巧妙的，就是先预先设计K个context场景，然后使用贝叶斯概率的方式将其耦合入最终点击的预测，某种意义上来说，就是先去预测每一个context下用户点击发生的概率，然后根据每一个context发生的概率对其进行一下加权求和，最终得到不同综合情况下用户的点击概率。

具体可以参考下图：

在这里插入图片描述

下面，我们首先来看一下loss的数学定义，然后来看一下文中给出的模型实际的构造方法。

1. loss定义

这里，模型的loss定义本质上就是如下条件表达式:

$\begin{aligned} P_{\theta}(Y|do(S)) &= P_{\theta}(Y|S,C) \\ &= \sum\limits_{i=1}^{|C|} P_{\theta}(Y|S,C=c_i) \cdot P(C=c_i) \end{aligned}$

而通过附录B中给出的推导，我们可以使用Jensen不等式直接将上式放缩为：

$P_{\theta}(Y|do(S)) \geq E_{c\sim Q(C|S=S)} [logP_{\theta}(Y|S=S,C=c)] - D_{KL}(Q(C|S=S) || P(C))$

其中， $Q (C ∣ S = S)$ 为模型拟合的在行为序列 $S$ 情况下场景（context） $C$ 的发生概率。

而关于 $P (C)$ 的计算，可以通过下述表达式来近似：

$\simeq \frac{1}{N}\sum\limits_{i=1}^{N}Q(C|S=S_i)$

当然，完整计算上式的复杂度太高，因此文中对其进行了简化，只从中sample了一些样本进行近似拟合：

$\simeq \frac{1}{R}\sum\limits_{j=1}^{R}Q(C|S=S_j)$

其中 $\ll N$ 。

由此，我们事实上就将上述loss表达式完全转换成了 $P_{\theta}(Y|S,C=c_i)$ 与 $Q (C ∣ S)$ 的表达式了。

因此，我们只需要用模型给出 $P_{\theta}(Y|S,C=c_i)$ 与 $Q (C ∣ S)$ 即可。

2. 模型设计

下面，我们来看一下文中给出的具体模型设计。

首先，文中对于行为序列中的每一个行为的embedding映射倒是一个非常简单的行为，就是一个基础的one-hot embedding的lookup，记作：

$h_m^1 = \mathop{OneHot}(x_m)^T \cdot H_x$

然后，通过一个神经网络（比如RNN或者Self-Attention网络），可以将其投影到一个输出的embedding：

$\begin{aligned} [h_1^2, h_2^2, ..., h_t^2] &= \Phi([h_1^1, h_2^1, ..., h_t^1], c(t); \Theta) \\ &= \sum\limits_{k=1}^{K}c(t)[k] \cdot \Phi_k([h_1^1, h_2^1, ..., h_t^1]; \Theta_k) \end{aligned}$

其中，关于 $c (t) [k]$ 的计算，文中是一个attention层的输出 $q_t$ 来进行模拟的，具体而言，就是将输入向量 $h_t$ 映射到 $k$ 个归一化权重上：

$q_t = \Psi(h_t^1; \Omega)$

其中 $\sum\limits_{k=1}^{K}q_k = 1$ 。

具体其中的映射关系为：

$\begin{aligned} q_t[k] &= \frac{exp((s_{tk} + g)/\tau)}{\sum\limits_{k=1}^{K}exp((s_{tk} + g)/\tau)} \\ s_{tk} &= a_k \cdot \mathop{tanh}(W_k \cdot h_t) \end{aligned}$