Week 6 hw3-1 全连接网络反向传播推导

折腾了半天，记录一下。

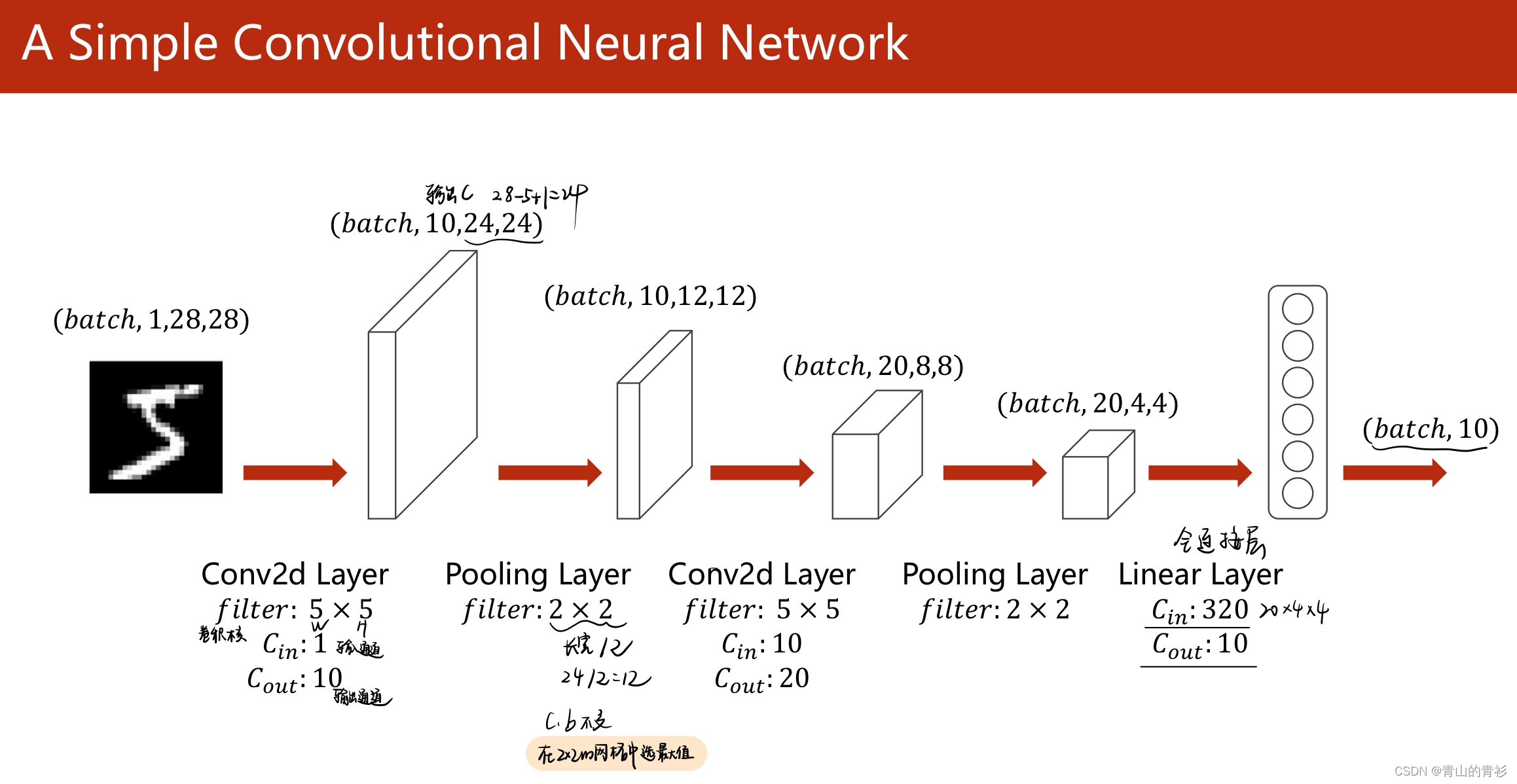
作业中网络由若干全连接层+ReLU组成，输出层的函数为softmax，损失函数为交叉熵。

一、记号

设网络有$n$层。如图，当$i<n$时，我们有如下几条式子成立：
$$\{\begin{array}{l}{z}_j^{i-1}=\text{ReLU}(x_j^{i-1})\\ x_j^i=\text{ReLU}({\hat{z}}_j^{i-1})\\ {\hat{z}}_j^{i-1}=\sum _{k=1}^{d_{i-1}}{z}_k^{i-1}{w}_{kj}^{i-1}+b_j^{i-1}\end{array}$$
同时，记：
$$\{\begin{array}{l}{\mathbf{x}}^{i-1}=[x_1^{i-1},x_2^{i-1},\dots ,x_{d_{i-1}}^{i-1}]\\ {\mathbf{x}}^i=[x_1^{i-1},x_2^{i-1},\dots ,x_{d_i}^i]\\ {\mathbf{z}}^{i-1}=[z_1^{i-1},z_2^{i-1},\dots ,z_{d_{i-1}}^{i-1}]\\ {\hat{\mathbf{z}}}^{i-1}=[{\hat{z}}_1^{i-1},{\hat{z}}_2^{i-1},\dots ,{\hat{z}}_{d_i}^{i-1}]\\ {\mathbf{b}}^{i-1}=[b_1^{i-1},b_2^{i-1},\dots ,b_{d_i}^{i-1}]\\ {\mathbf{W}}^{i-1}=\left(\begin{array}{cccc}{w}_{11}^{i-1}& w_{12}^{i-1}& \dots & w_{1d_i}^{i-1}\\ w_{21}^{i-1}& w_{22}^{i-1}& \dots & w_{2d_i}^{i-1}\\ ⋮& ⋮& \ddots & ⋮\\ w_{d_{i-1}1}^{i-1}& w_{d_{i-1}2}^{i-1}& \dots & w_{d_{i-1}{d}_i}^{i-1}\end{array}\right)\end{array}$$

那么我们得到矩阵形式：
$$\{\begin{array}{l}{\mathbf{z}}^{i-1}=\text{ReLU}({\mathbf{x}}^{i-1})\\ {\mathbf{x}}^i=\text{ReLU}({\hat{\mathbf{z}}}^{i-1})\\ {\hat{\mathbf{z}}}^{i-1}={\mathbf{z}}^{i-1}{\mathbf{W}}^{i-1}+{\mathbf{b}}^{i-1}\end{array}$$
当$i=n$时，记$i$位置的真实标签为$y_i$，预测结果为${\hat{y}}_i$。我们有：
$$\{\begin{array}{l}{z}_j^{n-1}=\text{ReLU}(x_j^{n-1})\\ {\hat{y}}_j=[\text{softmax}({\hat{z}}_1^{n-1},{\hat{z}}_2^{n-1}\dots ,{\hat{z}}_{d_n}^{n-1}){]}_j\\ {\hat{z}}_j^{n-1}=\sum _{k=1}^{d_{n-1}}{z}_k^{i-1}{w}_{kj}^{n-1}+b_j^{n-1}\end{array}$$
记$\mathbf{y}=[y_1,y_2,\dots ,y_{d_n}],\hat{\mathbf{y}}=[{\hat{y}}_1,{\hat{y}}_2,\dots ,{\hat{y}}_{d_n}]$。其中$\mathbf{y}$为one-hot向量。

那么我们得到矩阵形式：
$$\{\begin{array}{l}{\mathbf{z}}^{n-1}=\text{ReLU}({\mathbf{x}}^{n-1})\\ \hat{\mathbf{y}}=\text{softmax}({\hat{\mathbf{z}}}^{n-1})\\ {\hat{\mathbf{z}}}^{n-1}={\mathbf{z}}^{n-1}{\mathbf{W}}^{n-1}+{\mathbf{b}}^{n-1}\end{array}$$
记损失函数$J(\mathbf{y},\hat{\mathbf{y}})=-\sum _{i=1}^{d_n}{y}_i\log {\hat{y}}_i$。

二、推导

接下来计算$\nabla J_{{\mathbf{W}}^l}$与$\nabla J_{{\mathbf{b}}^l}$。

画出计算图，得到：
$$\begin{gathered} \nabla J_{w_{ij}^l}=\frac{\partial J}{\partial {\hat{z}}_j^l}\frac{\partial {\hat{z}}_j^l}{\partial w_{ij}^l}=\frac{\partial J}{\partial {\hat{z}}_j^l}{z}_i^l \\ \nabla J_{b_j^l}=\frac{\partial J}{\partial {\hat{z}}_j^l}\frac{\partial {\hat{z}}_j^l}{\partial b_j^l}=\frac{\partial J}{\partial {\hat{z}}_j^l} \end{gathered}$$

写成矩阵形式，得到：
$$\begin{gathered} \nabla J_{{\mathbf{W}}^l}=({\mathbf{z}}^l{)}^T\nabla J_{{\hat{\mathbf{z}}}^l} \\ \nabla J_{{\mathbf{b}}^l}=\nabla J_{{\hat{\mathbf{z}}}^l} \end{gathered}$$
于是只需要计算$\nabla J_{{\hat{\mathbf{z}}}^l}$即可。我们尝试构造递推式计算。画出计算图，得到：
$$\nabla J_{{\hat{z}}_j^l}=(\sum _{k=1}^{d_{l+1}}\frac{\partial J}{\partial {\hat{z}}_k^{l+1}}\frac{\partial {\hat{z}}_k^{l+1}}{\partial x_j^{l+1}})\frac{\partial x_j^{l+1}}{\partial {\hat{z}}_j^l}=(\sum _{k=1}^{d_{l+1}}\frac{\partial J}{\partial {\hat{z}}_k^{l+1}}{w}_{jk}^{l+1}){\frac{\text{d ReLU}}{\text{d}x}|}_{x={\hat{z}}_j^l}$$
写成矩阵形式，得到：
$$\nabla J_{{\hat{\mathbf{z}}}^l}=\nabla J_{{\hat{\mathbf{z}}}^{l+1}}{\mathbf{W}}^{l+1}\text{ReLU’}({\hat{\mathbf{z}}}^l)$$
因此若得到$\nabla J_{{\hat{\mathbf{z}}}^{n-1}}$则完成计算。下面计算$\nabla J_{{\hat{\mathbf{z}}}^{n-1}}$。

由于$\mathbf{y}$为one-hot向量，若真实标签的类别为$i$，那么我们有$J(\mathbf{y},\hat{\mathbf{y}})=-y_i\log {\hat{y}}_i=-\log {\hat{y}}_i$。

画出计算图，得到：
$$\nabla J_{{\hat{z}}_j^{n-1}}=\frac{\partial J}{\partial {\hat{z}}_j^{n-1}}=\sum _{k=1}^{d_n}\frac{\partial J}{\partial {\hat{y}}_k}\frac{\partial {\hat{y}}_k}{\partial {\hat{z}}_j^{n-1}}=\frac{\partial J}{\partial {\hat{y}}_i}\frac{\partial {\hat{y}}_i}{\partial {\hat{z}}_j^{n-1}}=-\frac{1}{{\hat{y}}_i}\frac{\partial {\hat{y}}_i}{\partial {\hat{z}}_j^{n-1}}$$
由于${\hat{y}}_i=\frac{\exp ({\hat{z}}_i^{n-1})}{{\sum }_{k=1}^{d_n}\exp ({\hat{z}}_k^{n-1})}$，下面进行分类讨论。

当$i\ne j$时，有：
$$\frac{\partial {\hat{y}}_i}{\partial {\hat{z}}_j^{n-1}}=-\frac{\exp ({\hat{z}}_i^{n-1})}{({\sum }_{k=1}^{d_n}\exp ({\hat{z}}_k^{n-1}){)}^2}\exp ({\hat{z}}_j^{n-1})=-{\hat{y}}_i{\hat{y}}_j$$
当$i=j$时，有：
$$\frac{\partial {\hat{y}}_i}{\partial {\hat{z}}_j^{n-1}}=\frac{\sum _{k=1,k\ne i}^{d_n}\exp ({\hat{z}}_k^{n-1})}{(\sum _{k=1}^{d_n}\exp ({\hat{z}}_k^{n-1}){)}^2}\exp ({\hat{z}}_i^{n-1})=(1-{\hat{y}}_i){\hat{y}}_i$$
代入$\nabla J_{{\hat{z}}_j^{n-1}}$，我们得到：
$$\nabla J_{{\hat{z}}_j^{n-1}}=\{\begin{array}{ll}{\hat{y}}_j,& i\ne j\\ -1+{\hat{y}}_j,& i=j\end{array}$$
至此推导完毕。