Problem: 437. 路径总和 III

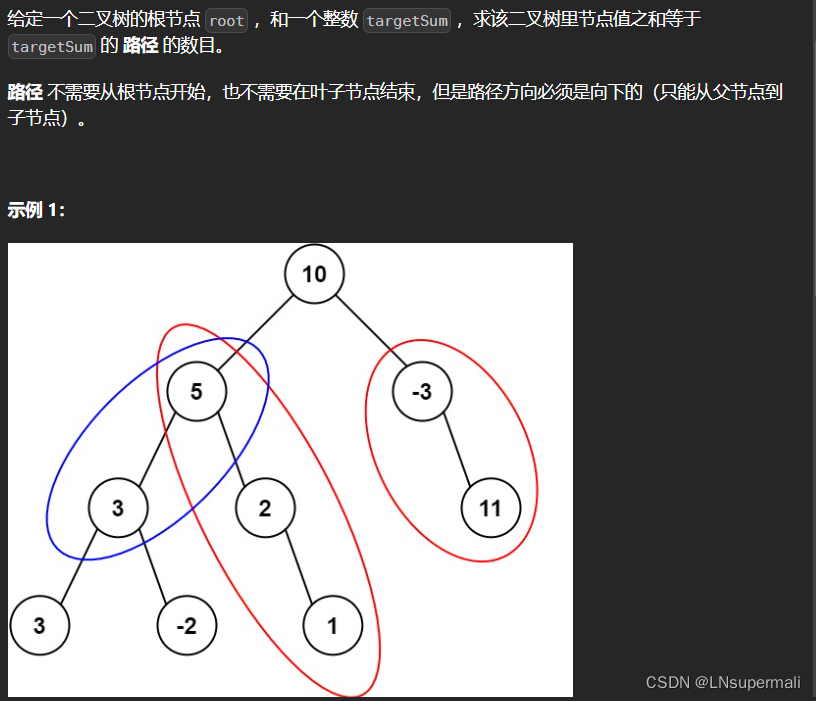
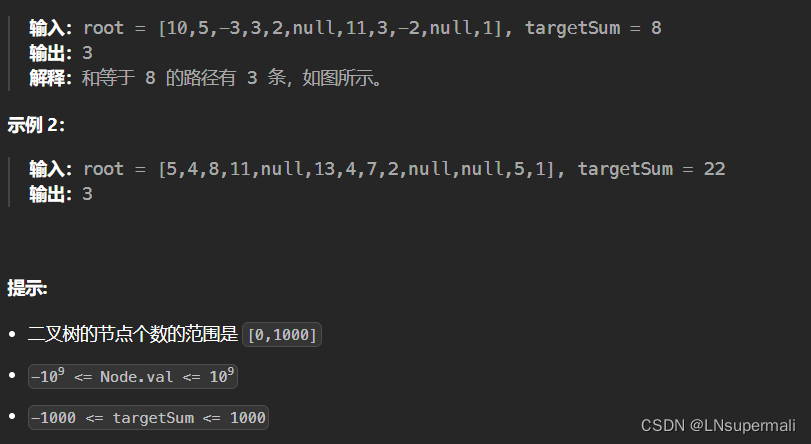
题目描述

思路

1.定义int类型函数rootSum(root, targetSum)，用于求取每一个节点等于目标函数的路径数：

1.1.易知rootSum(root, targetSum)求出的数量等于rootSum(root.left, targetSum - value)求出的数量加上rootSum(root.right, targetSum - value)求出的数量,其中value是当前遍历到的节点的节点值
1.2.若当前的value值等于targetSum，则所求的路径总和加一；

2.在pathSum函数中实现对每一个节点调用rootSum函数得出最终的路劲总和数

复杂度

时间复杂度:

$O(n^2)$;其中$n$为二叉树节点的个数

空间复杂度:

$O(n)$

Code

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    /**
     * Path Sum III
     *
     * @param root      The root of binary tree
     * @param targetSum The target number
     * @return int
     */
    public int pathSum(TreeNode root, long targetSum) {
        if (root == null) {
            return 0;
        }
        int res = rootSum(root, targetSum);
        res += pathSum(root.left, targetSum);
        res += pathSum(root.right, targetSum);
        return res;
    }

    /**
     * Find the sum of the target paths of each node
     *
     * @param root      The root of binary tree
     * @param targetSum The target number
     * @return int
     */
    public int rootSum(TreeNode root, long targetSum) {
        int res = 0;
        if (root == null) {
            return 0;
        }
        int value = root.val;
        if (value == targetSum) {
            res++;
        }
        res += rootSum(root.left, targetSum - value);
        res += rootSum(root.right, targetSum - value);
        return res;
    }
}