文章目录
- 二分法求解
- 最小二乘法曲线拟合
- 最小二乘法的来历
- 最小二乘法与曲线拟合
- 多项式曲线拟合
- SciPy内置最小二乘法应用
- 泰勒级数
- 背景引入
- 泰勒公式
- 泰勒级数展开与多项式近似
二分法求解
机器学习过程中往往会用到很多变量,而这些变量之间的复杂关系一般用非线性方程来,描述。但是,很多非线性方程的求解过程比较繁琐,且没有解析解。为此我们通常近似或者逼近等方法进行求解。二分法`(Bisection Method)和牛顿法(Newton's Method)等都是典型的求解非线性方程近似根的方法。
利用二分法求解方程近似根的过程如下:
对于区间[a,b]上连续不断且f(a)*f(b)<0的函数y=f(x),通过不断地把函数的零点区间一分为二,是区间的两个端点逐步逼近零点,从而得到零点近似值。
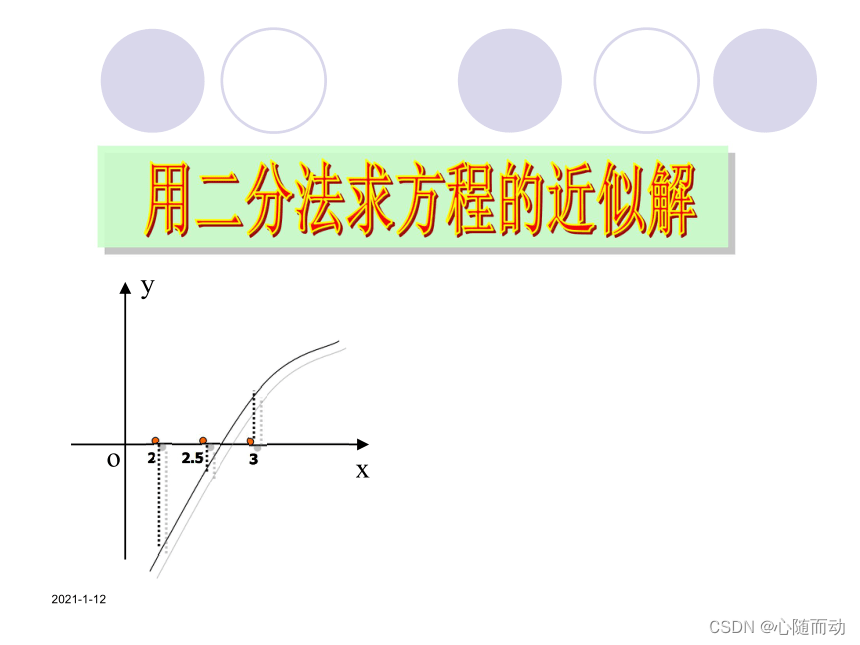
给定进度e,用二分法求解零点的步骤如下:
①.确定区间[a,b],验证f(a)*f(b)<0。
②.计算f((a+b)/2),若f((a+b)/2)=0,则(a+b)/2为零点。
③.若f(a)*f((a+b)/2)<0,则零点属于(a,(a+b)/2)区间。
若f(b)*f((a+b)/2)<0,则零点属于((a+b)/2,b)区间。
④.判断是否达到给定精度,若|a-b|<e,则得到零点的近似值a或b,否则重复步骤②~④
以下为二分法求解方程的示例代码:
import numpy as np
f0=lambda x:2**x-4
f1=lambda x:np.log10(x)
f2=lambda x:x**0.5-1
f3=lambda x:x**2-x*2-1
#定义二分求解函数
def bisection(a,b,fun):
sec=(a+b)/2
while True:
if fun(sec)*fun(a)<0:
b=sec
elif fun(sec)*fun(a)<0:
a=sec
else:
return sec
least_sec=sec
sec=(a+b)/2
try:
if abs((sec-least_sec)/sec)<0.000005:
return sec
except ZeroDivisionError as e:
pass
pass
print(bisection(-5,5,f0))
print(bisection(0.5,5,f1))
print(bisection(0,15.0,f2))
print(bisection(-10,12.0,f3))
结果展示:
0.0 0.78125 0.9375 -4.5
最小二乘法曲线拟合
作为一种常见的数学优化方法,最小二乘法也被称为最小平方法(Least Square Methord,LSM)。他主要通过最小化误差的平方和寻找数据的最佳函数匹配。利用最小二乘法可以渐变的求得未知数据,并使这些求得的数据与实际数据之间误差的平方和最小。最小二乘法常用于曲线拟合,线性回归预测,以及其他数理统计等应用场景。
最小二乘法的来历
对于著名的算法,从来不缺少有趣的故事。1801年,意大利亚天文学家朱塞普·皮亚齐(Giuseppe Piazzi)在西西里岛上发现了一颗小行星,并以西西里岛的保护神谷神(Ceres)来命名。随后一段时间,该小行星运行至太阳背面,许多科学家根据皮亚齐的数据寻找皆未果。有人说皮亚齐是故意散布这个消息来骗取名誉,皮亚齐一时之间有苦难言,因为该行星在太阳背面,望远镜根本不起作用,他也无法指出具体位置。时年24岁的德国著名数学家高斯(Gauss)也参与了寻找,并计算出谷神星的轨道。奥地利天文学家海因里希·奥尔伯斯(Heinrich Olbers)根据高斯计算出来的轨道重新发现了谷神星。1809年,高斯将计算轨道时使用的最小二乘法发表于其著作《天体运动论》中。
法国科学家勒让德(Legendre)于1806年独立发明的最小二乘法,但因为不为世人所知而默默无闻,他曾与高斯产生过谁是最早创造最小二乘法的人的争执。值得欣慰的是,源于天文学与测地学的最小二乘法,时至今日仍然在数理统计,机器学习以及人工智能领域大放光彩。
最小二乘法与曲线拟合
用连续曲线近似地刻画或比拟平面上离散点组所表示的坐标之间的函数关系的一种数据处理方法。用解析表达式逼近离散数据的一种方法。在科学实验或社会活动中,通过实验或观测得到量x与y的一组数据对(xi,yi)(i=1,2,…m),其中各xi是彼此不同的 。人们希望用一类与数据的背景材料规律相适应的解析表达式,y=f(x,c)来反映量x与y之间的依赖关系,即在一定意义下“最佳”地逼近或拟合已知数据。f(x,c)常称作拟合模型 ,式中c=(c1,c2,…cn)是一些待定参数。当c在f中线性出现时,称为线性模型,否则称为非线性模型。有许多衡量拟合优度的标准,最常用的一种做法是选择参数c使得拟合模型与实际观测值在各点的残差(或离差)ek=yk-f(xk,c)的加权平方和达到最小,此时所求曲线称作在加权最小二乘意义下对数据的拟合曲线。有许多求解拟合曲线的成功方法,对于线性模型一般通过建立和求解方程组来确定参数,从而求得拟合曲线。至于非线性模型,则要借助求解非线性方程组或用最优化方法求得所需参数才能得到拟合曲线,有时称之为非线性最小二乘拟合。 [1]
曲线拟合:贝塞尔曲线与路径转化时的误差。值越大,误差越大;值越小,越精确。
多项式曲线拟合
多项式曲线拟合(Polynomial Curve Fitting)是最小二乘法的一个最为典型的应用。

代码展示:
#多项式曲线拟合
#多项式曲线拟合
import numpy as np
import matplotlib.pyplot as plt
import random #随机数处理
#用来正常显示中文标签
plt.rcParams['font.sans-serif']=['SimHei']
#多项式的次数
m=7
#生成样本数据点
x=np.arange(-1,1,0.02)
y=[((a*a-1.55)**3+(a-0.3)**7+4*np.sin(5*a)) for a in x]
#可视化真实曲线
plt.plot(x,y,color='g',linestyle='--',marker='',label='Real Curve')
x_a=[b1*(random.randint(90,120))/100 for b1 in x]
y_a=[b2*(random.randint(90,120))/100 for b2 in y]
plt.plot(x_a,y_a,color='r',linestyle='',marker='.',label='Data Points')
'''
求解最小二乘法解析解
'''
#初始化二维数组
array_x=[[0 for i in range(m+1)] for i in range(len(x_a))]
#对数组进行赋值
for i in range(0,m+1):
for j in range(0,len(x_a)):
array_x[j][i]=x_a[j]**i
#将赋值后的二维数组转化为矩阵
matx=np.matrix(array_x)
matrix_A=matx.T*matx
yy=np.matrix(np.array(y_a))
matrix_B=matx.T*yy.T
#调用solve函数求解
mattAA=np.linalg.solve(matrix_A,matrix_B).tolist()
#计算拟合曲线
xxa=np.arange(-1,1.06,0.01)
yya=[]
#生成拟合曲线数据点
for i in range(0,len(xxa)):
yyy=0.0
for j in range(0,m+1):
dy=1.0
for k in range(0,j):
dy*=xxa[i]
dy*=mattAA[j][0]
yyy+=dy
yya.append(yyy)
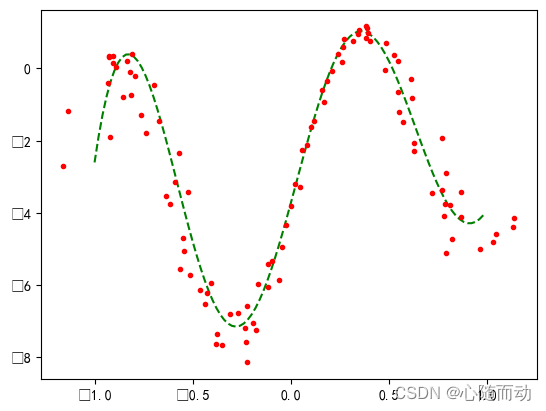
plt.plot(xxa,yya,color='b',linestyle='-',marker='',label='Fitted Curve')
plt.legend()
plt.show()
SciPy内置最小二乘法应用
因最小二乘法应用比较广,所以他也被很多模块作为内置函数。以科学计算工具包SciPy为例,其内置的函数的原型为:
leastsq(func, x0, args=(), Dfun=None, full_output=0, col_deriv=0, ftol=1.49012e-8, xtol=1.49012e-8, gtol=0.0, maxfev=0, epsfcn=None, factor=100, diag=None):
其中func函数是我们自己定义的一个误差函数,x0是计算的初始化数值,args用于指定func的其他参数。
该函数的实现代码:
def leastsq(x,y):
'''
x,y分别表示要拟合的数据的自变量和因变量
'''
meanx=sum(x)/len(x) #求x的平均值
meany=sum(y)/len(y)
xsum=0.0
ysum=0.0
for i in range(len(x)):
xsum+=(x[i]-meanx)*(y[i]-meany)
ysum+=(x[i]-meanx)**2
k=xsum/ysum
b=meany-k*meanx
return k,b
下列示例代码将利用leastsq()内置函数计算出拟合曲线的相关参数,并可视化拟合曲线,原示例函数曲线以及样本数据点。
import numpy as np
import scipy as sp
from scipy.optimize import leastsq
import pylab as plt
m=9 #多项式的次数
#定义一个示例函数
def real_func(x):
return np.sin(3*x**5+2*x**4)
#定义多项式用作拟合曲线
def fit_func(p,x):
f=np.poly1d(p)
return f(x)
#定义偏差函数
def reslduals(p,y,x):
return y-fit_func(p,x)
#随机选取10 个样本数据点
x=np.linspace(0,1,15)
#定义曲线可视化所需的数据点个数
x_show=np.linspace(0,1,1000)
y0=real_func(x)
#加入正态分布噪声后的数据点个数
y1=[np.random.normal(0,0.1)+y for y in y0]
#随机产生一组多项式分布的参数
p0=np.random.randn(m)
#利用内置的最小二乘法函数计算曲线拟合参数
plsq=leastsq(reslduals,p0,args=(y1,x))
#输出拟合参数
print('Fitting Parameters:',plsq[0])
#可视化拟合曲线,样本数据点以及缘函数曲线
plt.rcParams['font.sans-serif']=['SimHei']
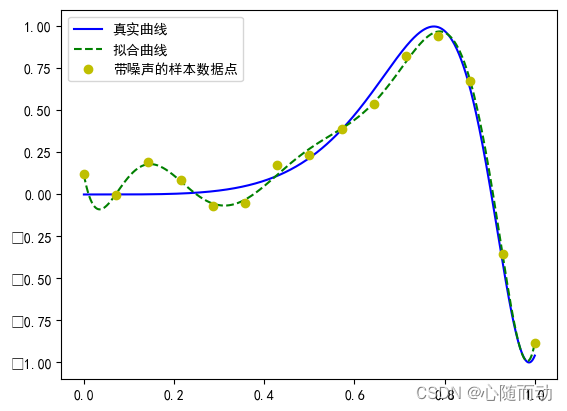
plt.plot(x_show,real_func(x_show),color='b',linestyle='-',marker='',label='真实曲线')
plt.plot(x_show,fit_func(plsq[0],x_show),color='g',linestyle='--',marker='',label='拟合曲线')
plt.plot(x,y1,'yo',label='带噪声的样本数据点')
plt.legend()
plt.show()
结果展示
泰勒级数
背景引入
开创了有限差分(Finite Difference)理论的英国数学家布鲁克·泰勒(Brook Taylor )式牛顿学派最优秀的代表人物之一,更是以泰勒级数(Taylor Series)和泰勒公式闻名世界。其主要著作为1715年出版的《正的和反的增量方法》(Methodus Incrementorum Directa et Inversa),其中记录了他于1712年发现的将函数展开成级数的著名的泰勒公式。
泰勒公式

泰勒级数展开与多项式近似
泰勒级数可将非常复杂的函数转变成多项式的形式,因此也称之为多项式近似(Polynomial Approximation)。通常,我们只需要计算泰勒级数前几项之和便可获得缘函数的局部相似。当然计算项越多,近似结果就越精确。
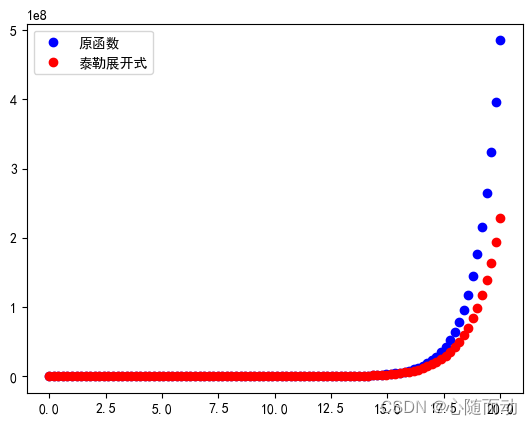
以下示例代码就演示了函数f(x)=e(x)与其N项泰勒展开多项式结果之间的比较。
#泰勒级数
import sympy
import numpy as np
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
#将x当作函数自变量
x=sympy.Symbol('x')
exp=np.e**x
#泰勒级数展开,对前N项进行求和
sums=0
N=20
for i in range(N):
#求i次导函数
numberator=exp.diff(x,i)
#计算导函数在x=0处的值
numberator=numberator.evalf(subs={x:0})
denominator=np.math.factorial(i)
sums+=numberator/denominator*x**i
#检验原函数与其在=0处展开的泰勒级数前20项之和
print(exp.evalf(subs={x:0})-sums.evalf(subs={x:0}))
xvals=np.linspace(0,20,100)
exp_points=np.array([])
sum_points=np.array([])
for xval in xvals:
#原数据点
exp_points=np.append(exp_points,exp.evalf(subs={x:xval}))
sum_points=np.append(sum_points,sums.evalf(subs={x:xval}))
#可视化结果
plt.plot(xvals,exp_points,'bo',label='原函数')
plt.plot(xvals,sum_points,'ro',label='泰勒展开式')
plt.legend()
plt.show()
如果采用不同的泰勒展开式项数进行近似计算,其效果也不相同。示例代码如下:
def PolynomialApproximation(func,num_terms):
'''
定义泰勒多项式近似函数
'''
sums=0
for i in range(num_terms):
numberator=func.diff(x,i)
numberator=numberator.evalf(subs={x:0})
denominator=np.math.factorial(i)
sums+=numberator/denominator*x**i
return sums
#获取泰勒展开式5项的近似曲线
sum5=PolynomialApproximation(exp,5)
sum10=PolynomialApproximation(exp,10)
#亦可直接利用SymPy模块内置的series函数获取泰勒展开式15项的近似曲线
sum15=exp.series(x,0,15).removeO()
xvals=np.linspace(5,10,100)
exp_points=[]
sum_5_points=[]
sum_10_points=[]
sum_15_points=[]
for xval in xvals:
exp_points=np.append(exp_points,exp.evalf(subs={x:xval}))
sum_5_points=np.append(sum_5_points,sum5.evalf(subs={x:xval}))
sum_10_points=np.append(sum_10_points,sum10.evalf(subs={x:xval}))
sum_15_points=np.append(sum_15_points,sum15.evalf(subs={x:xval}))
plt.plot(xvals,exp_points,'k-',label='原函数')
plt.plot(xvals,sum_5_points,'r*',label='5项泰勒展开式')
plt.plot(xvals,sum_10_points,'gd',label='10项泰勒展开式')
plt.plot(xvals,sum_15_points,'bo',label='15项泰勒展开式')





![[iHooya]1月15日寒假班作业解析](https://img-blog.csdnimg.cn/c430bcda67d442ba8c8b982909add71e.png#pic_center)