过滤多余的空格
一个句子中也许有多个连续空格，过滤掉多余的空格，只留下一个空格。

输入：一行，一个字符串（长度不超过200），句子的头和尾都没有空格。
输出：过滤之后的句子。
样例输入Hello world.This is c language.
样例输出Hello world.This is c language.

#include<bits/stdc++.h>
using namespace std;
//字符串写法
int main()
{
	string s;
	getline(cin,s);
	for(int i=0;i<s.length();i++)
		if(s[i]!=' '||(s[i]==' '&&s[i+1]!=' '))
			cout<<s[i];		
	return 0;
}

#include<bits/stdc++.h>
using namespace std;
//字符串写法
int main()
{
	char arr[201];
	cin.getline(arr,201);
	for(int i=0;i<strlen(arr);i++)
		if(s[i]!=' '||(s[i]==' '&&s[i+1]!=' '))
			cout<<s[i];		
	return 0;
}

---

爬楼
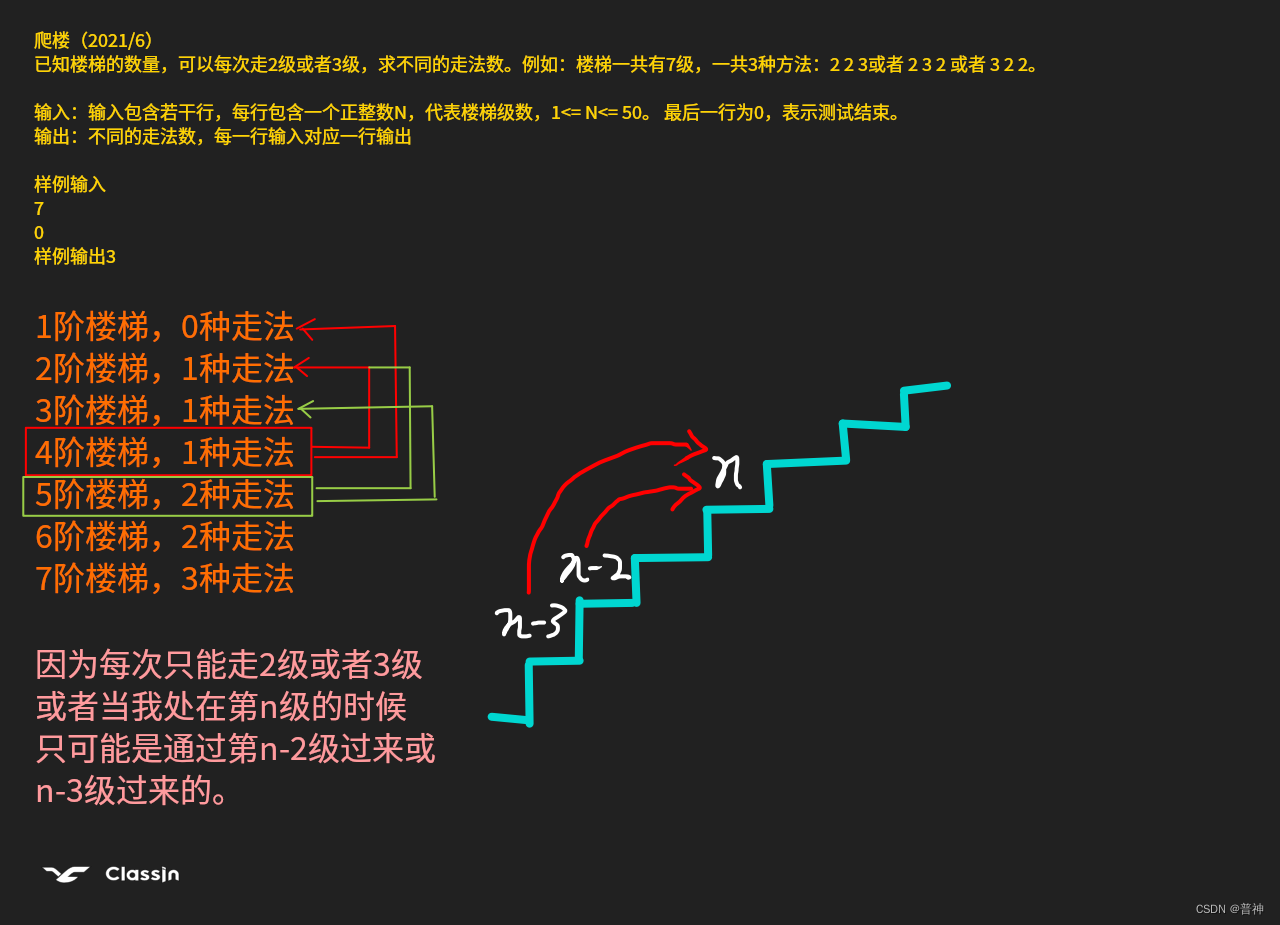
已知楼梯的数量，可以每次走2级或者3级，求不同的走法数。例如：楼梯一共有7级，一共3种方法：2 2 3或者 2 3 2 或者 3 2 2。

输入：输入包含若干行，每行包含一个正整数N，代表楼梯级数，1<= N<= 50。 最后一行为0，表示测试结束。
输出：不同的走法数，每一行输入对应一行输出

样例输入
7
0
样例输出3

#include <bits/stdc++.h>
using namespace std;

int pl(int n)
{
	if (n == 1)
		return 0;
	else if (n == 2)
		return 1;
	else if (n == 3)
		return 1;
	else
		return pl(n - 2) + pl(n - 3);
}
int main()
{
	int n;
//可以这样写
//	while (cin >> n)
//	{
//		cout << pl(n) << endl;
//	}
//也可以这样写
	while (1)
	{
		cin >> n;
		if (n == 0)
			break;
		cout << pl(n) << endl;
	}
	return 0;
}

---

爬楼梯
树老师爬楼梯，他可以每次走1级或者2级，输入楼梯的级数，求不同的走法数 例如：楼梯一共有3级，他可以每次都走一级，或者第一次走一级，第二次走两级 也可以第一次走两级，第二次走一级，一共3种方法。

输入：输入包含若干行，每行包含一个正整数N，代表楼梯级数，1 <= N <= 30
输出：不同的走法数，每一行输入对应一行输出

样例输入
5
8
10

样例输出
8
34
89

#include <iostream>
using namespace std;
//没啥可说的斐波那契数列
int N;
int stairs(int n)
{
	if( n < 0)
		return 0;
	if( n == 0 )
		return 1;
	return stairs(n-1) + stairs(n-2);
}
int main()
{
	while(cin >> N) {
		cout << stairs(N) << endl;
	}
	return 0;
}

---

踩方格
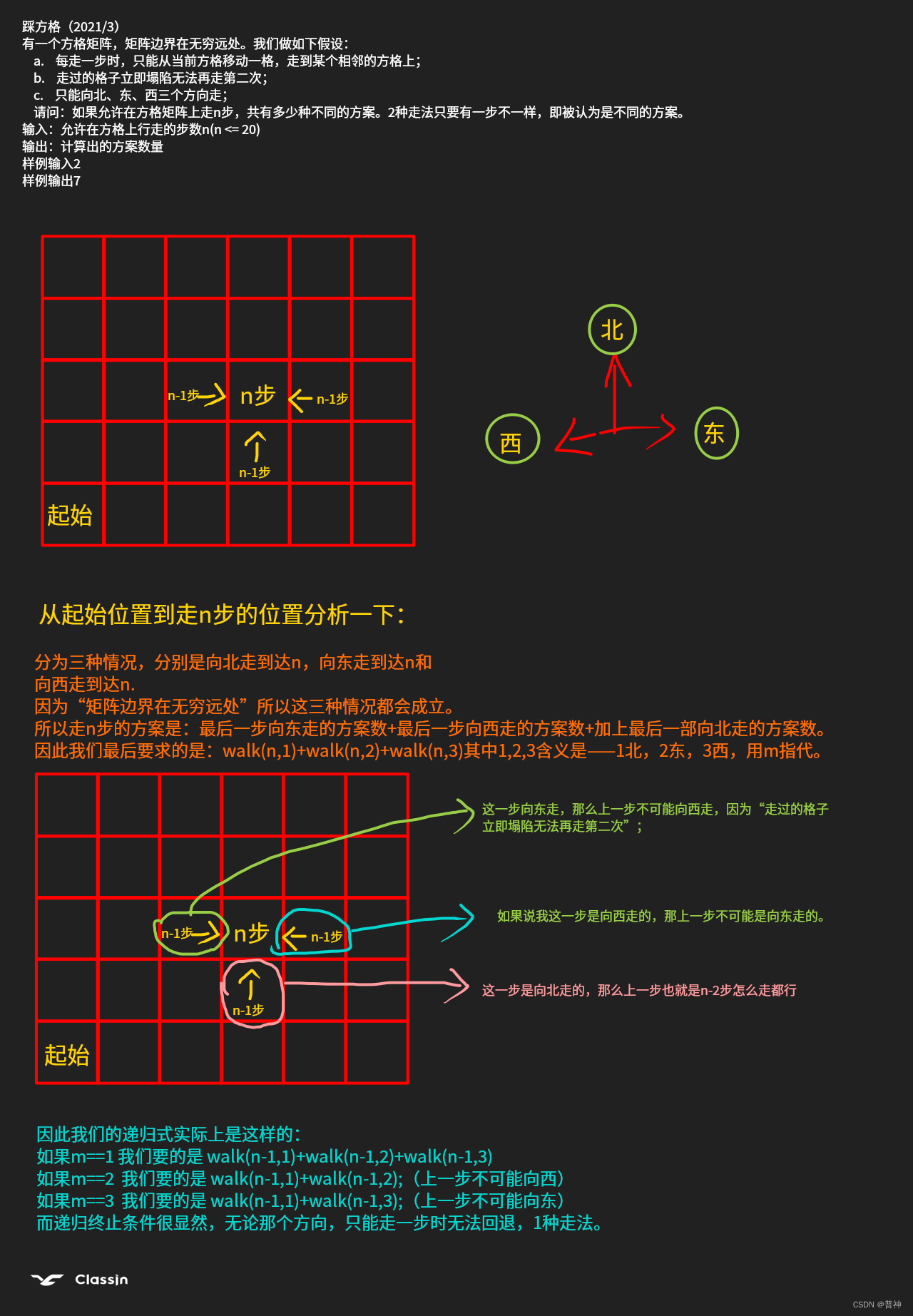
有一个方格矩阵，矩阵边界在无穷远处。我们做如下假设：
a. 每走一步时，只能从当前方格移动一格，走到某个相邻的方格上；
b. 走过的格子立即塌陷无法再走第二次；
c. 只能向北、东、西三个方向走；
请问：如果允许在方格矩阵上走n步，共有多少种不同的方案。2种走法只要有一步不一样，即被认为是不同的方案。

输入：允许在方格上行走的步数n(n <= 20)
输出：计算出的方案数量
样例输入2
样例输出7

#include <bits/stdc++.h>
using namespace std;

int walk(int n, int m)
{
	if (n > 1)
		if (m == 1)
			return walk(n - 1, 1) + walk(n - 1, 2) + walk(n - 1, 3);
		else if (m == 2)
			return walk(n - 1, 1) + walk(n - 1, 2);
		else if (m == 3)
			return walk(n - 1, 1) + walk(n - 1, 3);
		else if (n == 1)
			return 1;
}

int main()
{
	int n = 0;
	cin >> n;
	cout << walk(n, 1) + walk(n, 2) + walk(n, 3);
	return 0;
}