回溯法的题目太多了,不想写这个代码了,于是我就开始水一篇文章,就单纯的分析一下这个问题保持整本书完整的队形
问题描述
如何用有限的邮票数,贴出更多面额的需求?

举例
n=5,m=4
设计1:X1={1, 3, 11, 15, 32}
连续邮资区间{1, 2, 3, ……, 70}
设计2:X2={1, 6, 10, 20, 30}
邮资连续区间{1, 2, 3, 4}
问题分析
定义x[1:n]表示n种不同邮票的面值,并约定他们从小到大排列,x[1]=1是唯一的选择,因为最大邮资区间必须从1开始。
接下来x[2]的取值范围是[2:m+1],因为第一张是1,最多可以贴m张
于是可以推测:对于已经选定的x[1:i-1],最大的连续邮资区间是[1:r],那么接下来x[i]的取值范围是[+1 : r+1],若Xi>r+1, 则邮资r+1无法支付(约束条件)
在用回溯法解题目时,解空间树中各个节点的儿子是动态变化的,随着x的取值不同而变化
r 怎么计算呢? yi(j) 表示最多用 m 张面值 xi 的邮票贴出邮资 j 所需要的最少邮票张数

计算X[1:i]的最大连续邮资区间在本算法中被频繁使用到,因此势必要找到一个高效的方法。
考虑到直接递归的求解复杂度太高,我们不妨尝试计算用不超过m张面值为x[1:i]的邮票贴出邮资k所需的最少邮票数y[k]。通过y[k]可以很快推出r的值。
//x[i-2]*(m-1)是第i-2层循环的一个上限,目的是找到r-1的值
for (int j=0; j<= x[i-2]*(m-1);j++)
if (y[j]<m)
//k是对表示j剩余的票数进行检查
for (int k=1;k<=m-y[j];k++)
//x[i-1]*k是k张邮票能表示的最大邮资
//+j表示增加了i邮资后能
//判断新增加的能表示的邮资需要多少
if (y[j]+k<y[j+x[i-1]*k])
y[j+x[i-1]*k]=y[j]+k; //对第i-2层扩展一个x[i-1]后的邮资分布
//向后寻找最大邮资值,查看邮资范围扩大多少,然后查询y数组从而找到r
while (y[r]<maxint)
r++; //计算X[1:i]的最大连续邮资区间回溯函数

定义一些必要的变量

伪代码

代码(我抄的)
#include <stdio.h>
#define maxl 1000 //表示最大连续值
#define maxint 32767
int n, m; // n为邮票种类数,m为能贴的最大张数
int maxvalue; //表示最大连续值
int bestx[100]; //表示最优解
int y[maxl]; // y[k],存储表示到k值,所使用的最少邮票数
int x[100]; //存储当前解
void backtrace(int i, int r);
int main(){
printf("请输入邮票面值数:");
scanf("%d", &n);
printf("请输入能张贴邮票的最大张数:");
scanf("%d", &m);
for (int i = 0; i <= n; i++){
x[i] = 0;
bestx[i] = 0;
}
for (int i = 0; i < maxl; i++) y[i] = maxint;
x[1] = 1;
y[0] = 0;
maxvalue = 0;
backtrace(1, 0);
printf("当前最优解为:");
for (int i = 1; i <= n; i++) printf("%d ", bestx[i]);
printf("\n最大连续邮资为:");
printf("%d", maxvalue);
return 1;
}
void backtrace(int i, int r){
//对上一层的邮资值数组进行更新,上限是x[i-1]*m
for (int j = 0; j <= x[i - 1] * m; j++){
if (y[j] < m){
//从只使用一个x[i]到使用m-y[i]个,即使用最多的最大值,降低邮票数
//k是对表示j剩余的票数进行检查
for (int k = 1; k <= m - y[j]; k++){
if (y[j] + k < y[j + x[i] * k]){
//如果前面的某一个情况加上k个x[i],所达到邮资值使用的邮票数少于原来的邮票数则更新
y[j + x[i] * k] = y[j] + k;
}
}
}
}
//向后寻找最大邮资值,查看邮资范围扩大多少,然后查询y数组从而找到r
while (y[r] < maxint){
r++; //计算X[1:i]的最大连续邮资区间
}
if (i == n){ // i=n表示到达叶子节点。
if (r - 1 > maxvalue){ //若大于最大值,则更新最优值与最优解
for (int k = 1; k <= n; k++){
bestx[k] = x[k];
}
maxvalue = r - 1;
}
return;
}
int z[maxl];
//由于每一层需要对多种情况进行运算,因此需要将上一层的邮资值数组保留
for (int k = 0; k < maxl; k++){
z[k] = y[k];
}
for (int j = x[i] + 1; j <= r; j++){ //对下一层进行运算
x[i + 1] = j;
backtrace(i + 1, r - 1);
for (int k = 0; k < maxl; k++)
y[k] = z[k];
}
}输入:
2,3
5,4
4,3
输出


附一些数据
n= 5 m=4 {1,3,11,15,32} 最大邮资为70
n=5 m=5 {1,4,9,31,51} 最大邮资为126
n=4 m=2 {1,3,5,6}最大邮资为12
n=3 m=4 {1,5,8}最大邮资为26
n=6 m=4{1,4,9,16,38,49}最大邮资为108
n=5 m=6{1,7,12,43,52}最大邮资为216
可以结束了-但是-他还可以用动态规划来解决
设不超过m张面值为x[1:i]的邮票贴出邮资j所需的最少邮票数为y[j]。通过y[j]可以很快推出r的值。事实上,y[j]可以通过递推在O(n)时间内解决:yi(j) 表示最多用 m 张面值 xi 的邮票贴出邮资 j 所需要的最少邮票张数
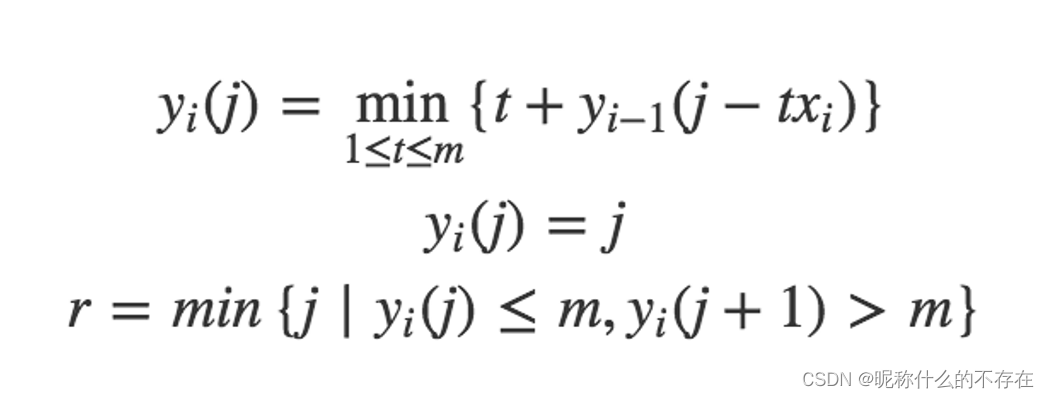
类似于0-1背包问题:
dfs(x,cur,max)其中x数组存储当前的解有哪些(如果你就是求具体数值,而不要求解的组成甚至可以省略),cur代表目前到第几种面值,当到n为止,max表示到目前为止的最大可到达邮资,而之后下一个x[cur+1]一定是取x[cur]+1~max+1,这个很好理解,max+1目前是访问不到的,那么我加入x[cur+1]后,要看看max更新到多少,而max是从max+1到
m*x[cur+1](最多就是m个最大的那个邮票,最少肯定是要更新,不然要你何用...),接下来的问题就是能否用n种邮票,面值都储存在x数组中,最多贴m张,表示出某个数,
方法是动态规划,状态转移方程dp[i,j]=min(dp[i-1][j-k*a[i]+k),其实有点像背包;(注意边界!!!!!!!)dp[i][0]=0(没有钱时0张邮票)dp[1][i]=i;(因为第一张邮票就是1,贴几块钱就是几张邮票)
#include <stdio.h>
#include <string.h>
int n,m;//n为邮票种类,m为一封信上最多贴的邮票个数
int Max;
int ans[10000];//最终答案数组
int min(int a,int b)
{
return a<b?a:b;
}
int panduan(int x[10000],int n,int sum)//能否用n种邮票,面值在x数组中,最多贴m张,表示出sum(是个动态规划问题,方法是求出dp[n][sum]看它是否小于sum,状态转移方程dp[i][j]=min(dp[i-1][j-k*x[i]]+k)(其中dp[i][j]表示用到第i种邮票,表示邮资为j的最少邮票
{
int i,j,k;
int dp[15][1005];
for (i=0;i<=n;i++)
dp[i][0]=0;
for (i=0;i<=sum;i++)
dp[1][i]=i;
for (i=2;i<=n;i++)
for (j=1;j<=sum;j++)
{
dp[i][j]=9999;
for (k=0;k<=j/x[i];k++)
dp[i][j]=min(dp[i][j],dp[i-1][j-x[i]*k]+k);
}
if (dp[n][sum]>m)
return 0;
return 1;
}
void DFS(int x[10000],int cur,int max)
{
int i,j,next;
if (cur==n)//如果已经得出了n种邮票
{
if (max>Max)//并且它的最大值已经大于当前最大邮资数
{
Max=max;
for (i=1;i<=cur;i++)
ans[i]=x[i];//更新答案数组
}
return;
}
for (next=x[cur]+1;next<=max+1;next++)//如果还没得到n中邮票,那么从x[cur]+1~max+1选一个作为下一个邮资,因为max+1没法表示,所以必定到max+1为止
{
x[cur+1]=next;//接下来是重点,用种类为cur+1,数目分别为x[1..cur+1]的邮票,最多使用m张,能否表示出大于max的某个数
for (i=max+1;i<=m*x[cur+1];i++)//这个数最少要为max+1(不然没有意义了),最多是x[cur+1]*m
if (panduan(x,cur+1,i)==0)//如果成立
break;
if (i>max+1)//如果至少让最大值更新了一次
DFS(x,cur+1,i-1);
}
}
int main()
{
int i,j,max,cur;
int x[1000];//中间传递的数组,存储当前的邮票值的解
scanf("%d%d",&n,&m);
Max=0;
max=m;
cur=1;
x[cur]=1;
DFS(x,cur,max);//x存储当前的解,cur表示当前传递到第几种邮票,max表示目前能表示到的最大值
printf("%d\n",Max);
for (i=1;i<=n;i++)
printf("%d ",ans[i]);
return 0;
}嘻嘻,抄完了,这个其实我没怎么搞懂,仅仅是大致搞明白了,特别是算r那个地方我不懂。
连续邮资问题详解_羊书change的博客-CSDN博客_连续邮资问题