阅读规范：

• 本文以重点为主，零碎知识点/相对不够重要的为辅助阅读内容，以脚注形式给出，点击脚注即可快速跳转。
• 助解题目通常是为了帮助理解给出的题目，考试不考，若已理解可直接跳过。
• 文中提到的课本是陈火旺的《编译原理第三版》。
• 习题的答案也统一用脚注给出（脚注位于习题后），点击脚注即可快速跳转，建议先自己思考，再看答案。
• 每章节后面会有综合题型，涵盖了本章节重点知识及算法，请完全掌握。
  

脚注使用：单击正文后的脚注标记即可跳转到详细，再次点击脚注详细内容后的返回箭头可以返回至正文阅读处

本文已开启Latex数学公式支持

正则文法：描述单词语法的文法

基本定义

• 正则文法，3型文法，分为右线性文法和左线性文法，重点掌握右线性文法。【快速跳转链接：3型文法¹、左线性文法¹】

  右线性文法：产生式形式为 $U\to xV|y$ 且 $U,V\in V_N，x,y\in V_T^{\ast }$
  

• 右线性文法G[S]的状态转换图（TG）表示

  • G[S]中的非终结符$V_N$作为TG的节点（用⚪表示）
    
  • G[S]的开始符号S对应状态转换图的开始状态S；（每个TG用$\to$指向开始状态）
    
  • 增加一个新状态$Z$，作为状态转换图的终止状态（用双圈表示）；
    
  • G[S]中形如$U\to xV$的每条产生式，画一条从状态U到状态V的方向弧，弧上的标记为x；
    
  • 对于G[S]中形如$U\to y$的每条产生式，画一条从状态U到终态Z的方向弧，弧上的标记为y
    

  【快速跳转链接：左线性文法的状态转换图表示²】

• 助解题目：给出与正则文法G(S)等价的状态转换图。【图】

正规式与正规集

• 正规式（正则表达式），对于字符集$\sum$，仅在$\sum$上包含()、|、*、·四种运算的正规式所表示的集合是$\sum$上的正规集

  【快速跳转链接：()、|、*、·四种运算运算规则 ³ 】

• 助解题目：$\sum =a,b$，其上的正规式与对应的正规集的例子：

正规式	正规集
$a|b$	{ a , b } \{a, b\} {a,b}
$(a|b{)}^{\ast }$	{ a , b } ∗ 即 a 和 b 所能构成的所有串的集合， { ϵ , a , b , a a , a b , b a , b b , a a a , . . . } \{a,b\}^*即a和b所能构成的所有串的集合，\{\epsilon, a, b, aa, ab, ba, bb, aaa, ...\} {a,b}∗即a和b所能构成的所有串的集合，{ϵ,a,b,aa,ab,ba,bb,aaa,...}
$a^{\ast }$	{ ϵ , a , a a , a a a , . . . } 即 0 或多个 a 的串组成的集合 \{\epsilon, a, aa, aaa, ...\}即0或多个a的串组成的集合 {ϵ,a,aa,aaa,...}即0或多个a的串组成的集合
$(a|b)(a|b)$	{ a a , a b , b a , b b } \{aa, ab, ba, bb\} {aa,ab,ba,bb}

【快速跳转链接：等价正规式 & 正规式等价变换 ⁴】

• 例子1：$a|b^{\ast }c$，它所表示的正规集为：串a或者是零个或多个b后跟随一个c，即 { a , c , b c , b b c , b b b c , . . . } \{a, c, bc, bbc, bbbc, ...\} {a,c,bc,bbc,bbbc,...}
• 例子2：求“每个1都有0直接跟在右边”的正规式：$(0|10{)}^{\ast }$
  • 思考方式：上述描述的基本结构是$10$，$(10{)}^{\ast }$表示的是 { ϵ , 10 , 1010 , . . . } \{\epsilon, 10, 1010,...\} {ϵ,10,1010,...}，在这个基本结构之上，0的位置是任意的，因此也就变成了“$10$与$0$的所有组合”，即$(0|10{)}^{\ast }$。
• 习题：(选择/填空)，课本 p64 8(1-4)

根据描述给出正规式

（1）以01结尾的二进制数串 ⁵

（2）能被5整除的十进制整数 ⁶

（3）包含奇数个1或奇数个0的二进制数串 ⁷

（4）英文字母组成的所有符号串，要求符号串中的字母按照字典序排列 ⁸

有限自动机（DFA、NFA）

DFA（确定的有限自动机）

• 五元组表示法

  • $M=(S,\Sigma ,f,S_0,Z)$

  1. $S$是一个非空有限集，它的每个元素称为一个状态
     
  2. $\Sigma$是一个有限的输入字母表，它的每个元素称为一个输入字符
     
  3. f是转换函数集，形如$f(k_i,a)=k_j(k_i\in S,k_j\in S，a\in \Sigma )$：当前状态为$k_i$，输入字符为a时，将转换到下一个状态$k_j$, $f$值唯一
     
  4. $S_0\in S$是唯一的一个初始状态；
     
  5. $Z\subseteq S$，是终止状态(终态)集合
     

  • 注意：初始状态只有一个、终态可以多个、f值唯一

• 状态转换图表示法

• 状态矩阵表示法

矩阵的行表示当前状态，列表示输入字符，矩阵元素表示相应状态行和输入字符列下的新状态。

• 助解题目：五元组与状态转换图互换ppt 3.3 23页】

NFA（非确定的有限自动机）

• 五元组表示法

  • $M=(S，\Sigma ，f，S_0，Z)$

  1. $S,\Sigma ,Z$的意义与DFA相同
     
  2. $f$与DFA中$f$的区别在于，对某个当前状态，对于输入字符a，可能有多个次态
     
  3. $S_0$表示的是初态集合，$S\subset 0$

  • 注意：初始状态可以有多个、终态可以多个，f值不唯一

• 状态转换图表示法

• 状态矩阵表示法

NFA与DFA联系与区别

• 区别：

初态：DFA只有一个，NFA有多个

状态转换函数$f$：DFA每个$f$值唯一确定，NFA每个$f$值可以有多个（次态集合）

有向弧：DFA中无$ϵ$弧，NFA中可能存在$ϵ$弧

• 联系：DFA是NFA的特例

NFA转DFA（NFA确定化）——子集构造法

• NFA确定化：通过某些操作消除NFA中$f$的多值性

• 必须掌握的三种运算，对于状态集$I$

  $\epsilon -closure(I)$——状态集的$\epsilon$闭包
  
  $move(I,a)$——状态集的$a$弧转换
  
  $I_a=\epsilon -closure(move(I,a))$——状态集的$a$弧转换的闭包$I_a$
  

  • $\epsilon -closure(I)$

    • 状态集$I$中的每个元素经过 $0或n条ϵ弧$ 能到达的所有状态的集合
      
    • 注：经过0条$ϵ$弧所能到达的状态即自己本身

  • $move(I,a)$

    • 状态集$I$中的每个元素经过 $1条a弧$ 能到达的所有状态的集合
      
    • 注意：仅经过1条a弧

  • $I_a=\epsilon -closure(move(I,a))$

    • 先求 $move(I,a)$ ， 记所得集合为 $M$
    • 再求 $\epsilon -closure(M)$

  • 习题：NFA的状态转换图如下，状态集 I = { 2 , 3 } I=\{2, 3\} I={2,3}，求$\epsilon -closure(I)$和$I_2$、$I_3$

    • 【图】
    • 答案⁹

• 方法论

  • 核心：构造状态转换矩阵， 形如

    $I$	$I_a$	$I_b$	…
    $T_0$	$\epsilon -closure(move(T_0,a))$	$\epsilon -closure(move(T_0,a))$	…
    $T_1$	$\epsilon -closure(move(T_1,a))$	$\epsilon -closure(move(T_1,a))$	…
    …	…	…	…

  • $(1)$ $T_0=\epsilon -closure(X)$，$X$是NFA的唯一初态。NFA的初态可能有多个，因此分以下两种情况讨论：

    • NFA初态唯一，且为$S_0$， $X=S_0$
    • NFA初态不唯一，则构造一个新状态$X$作为NFA的唯一初态，并通过一条$ϵ$弧指向初态集合$S_0$中的任意初态
    • 若NFA终态不唯一，则构造一个新状态$Y$作为NFA唯一终态，并将NFA中任意终态节点通过$ϵ$弧指向$Y$

  • $(2)$对NFA的状态转换图做如下等价变化：【图】【书p50】

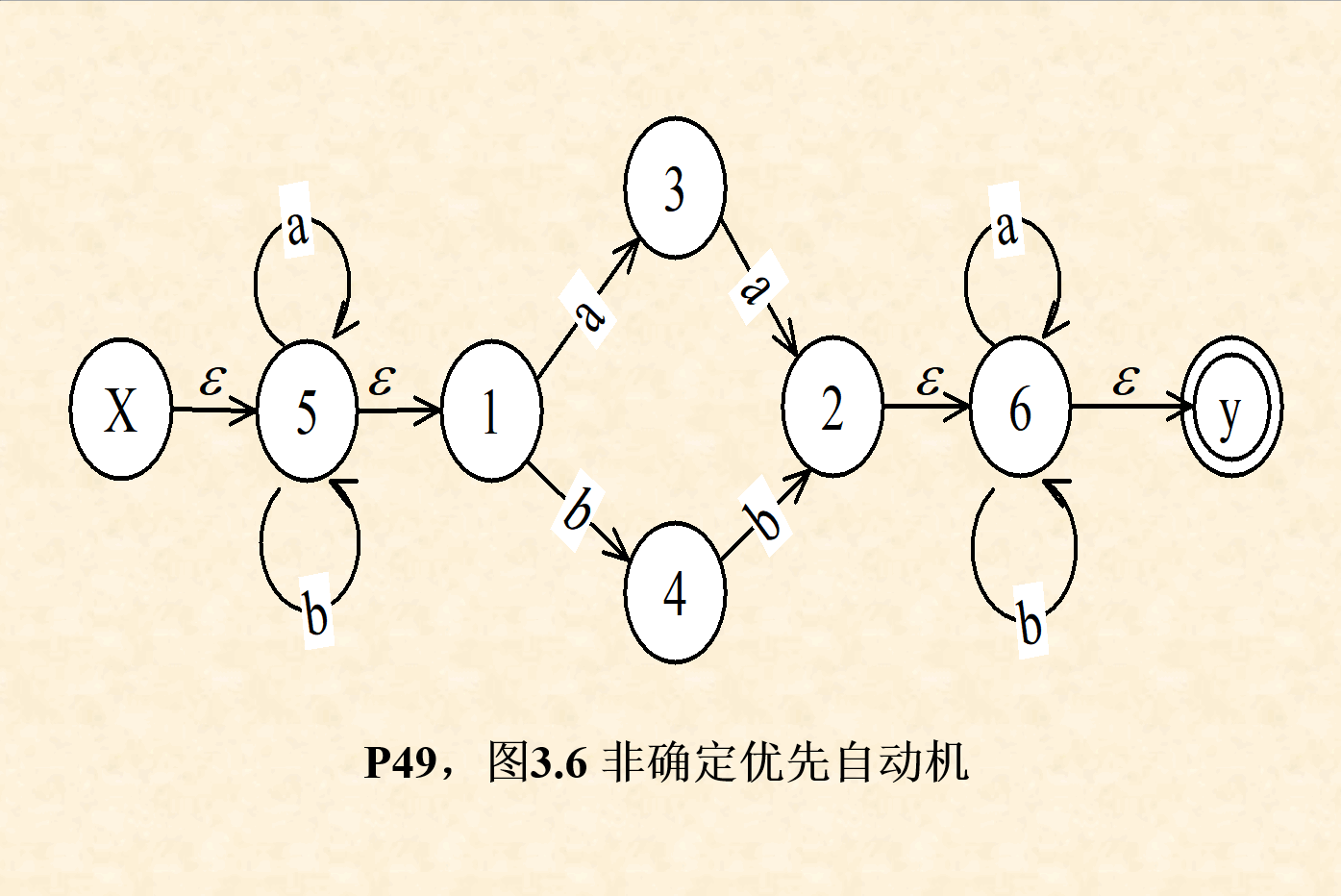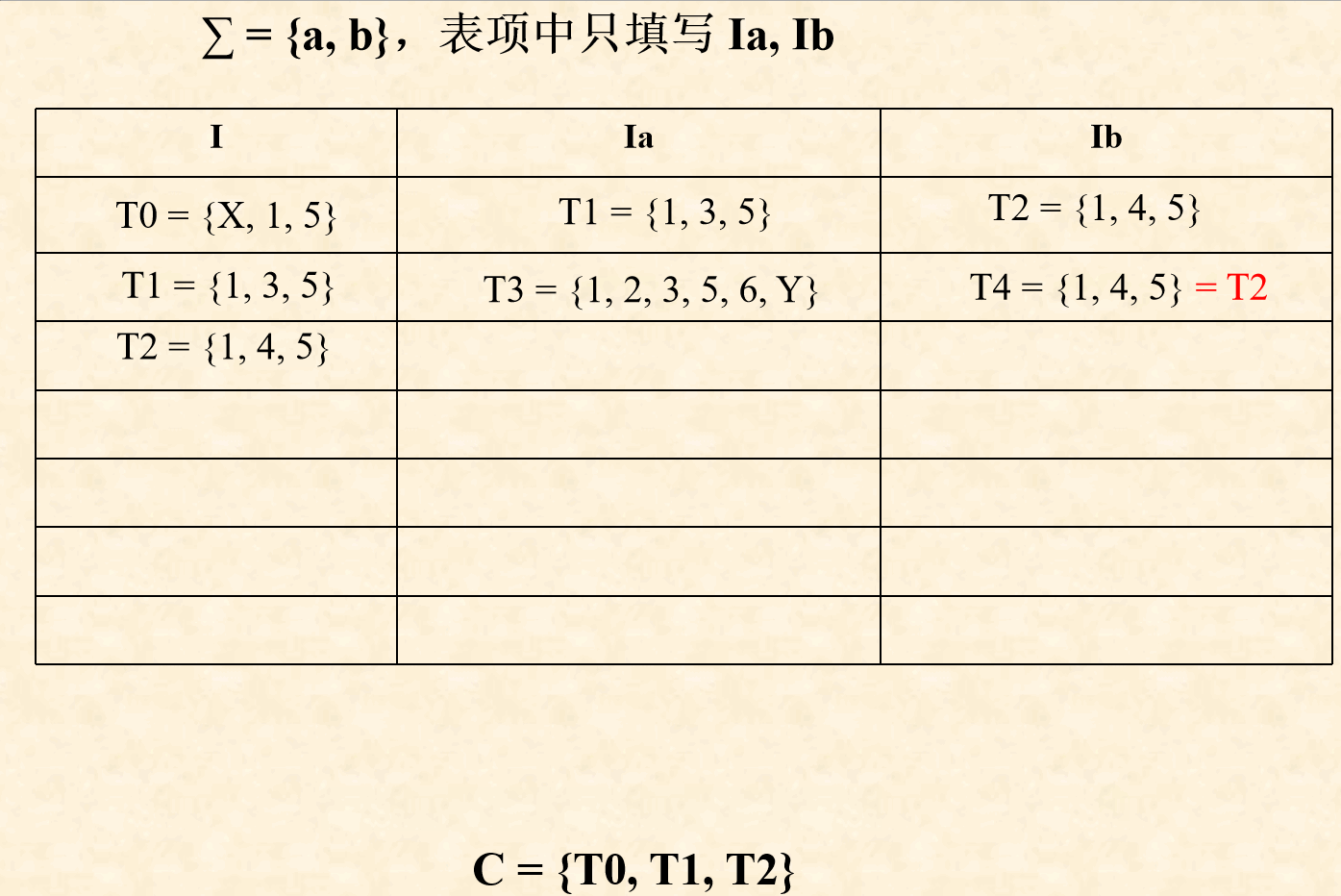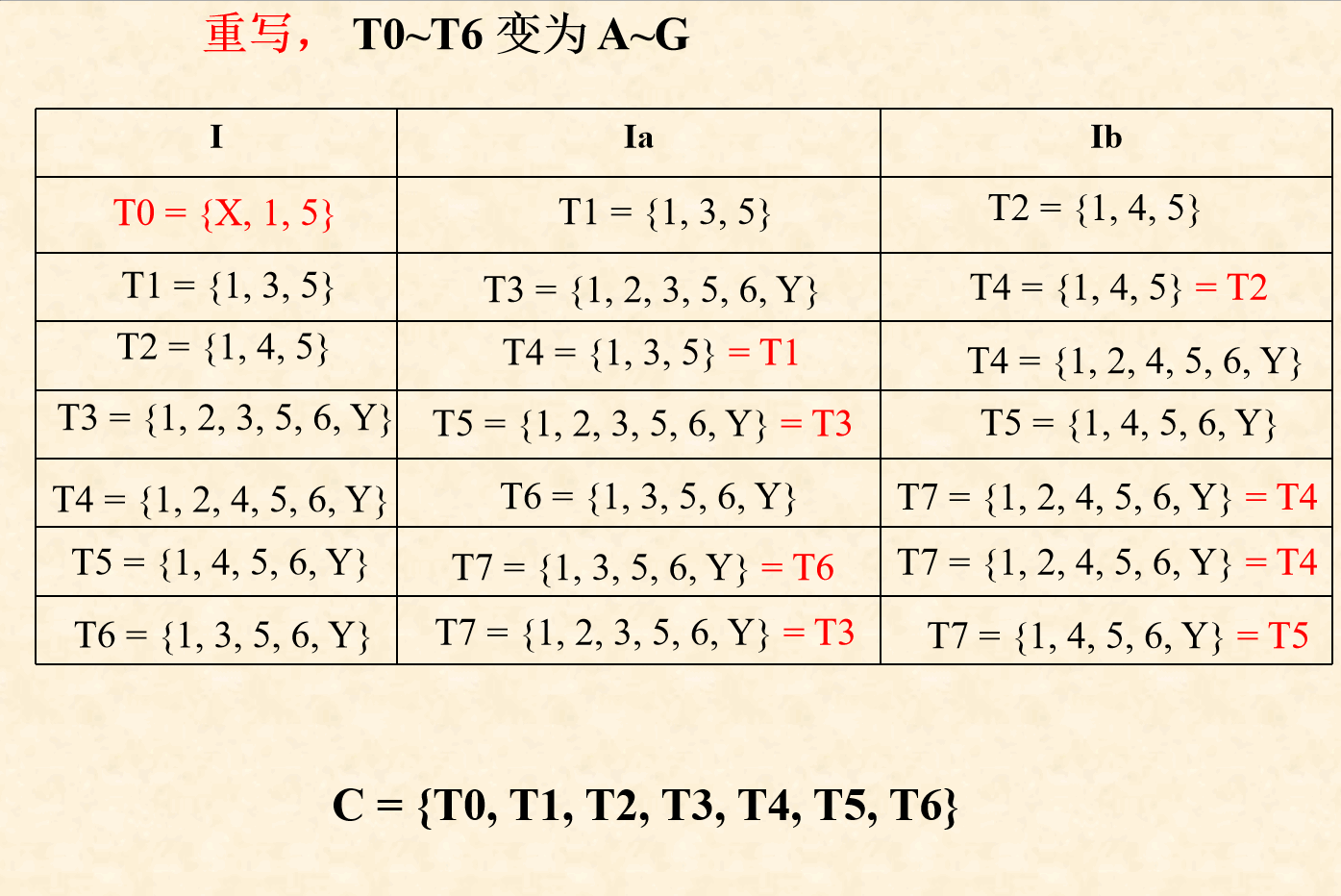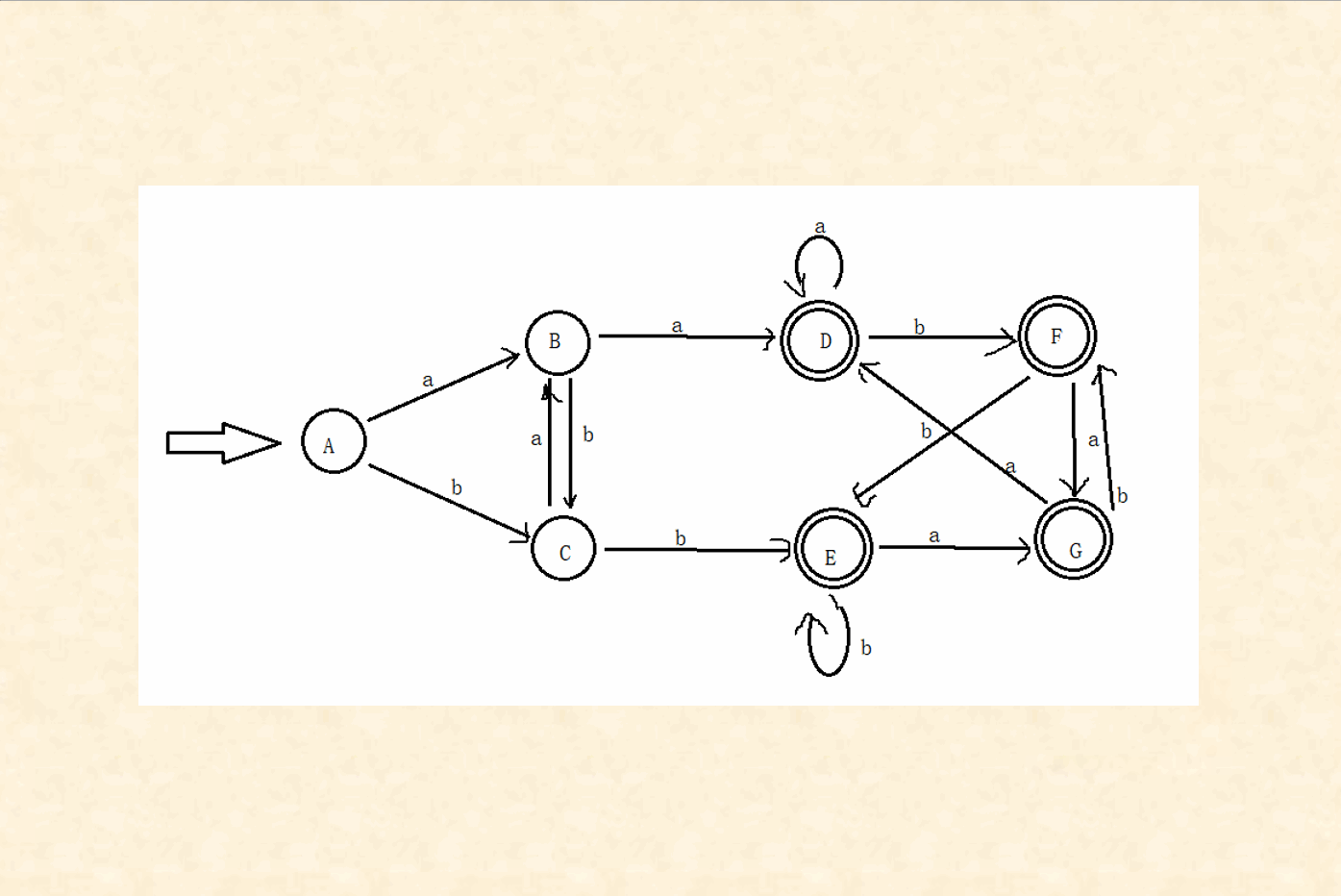
  • $(3)$用$C$表示新状态集合，开始构造状态转换矩阵时， C = { T 0 } C = \{T_0\} C={T0​}

  • $(4)$根据上表构造状态转换矩阵，对每个$T_j=\epsilon -closure(move(T_i,a))$

    • 若$T_j\notin C$，则 C = { T 0 , T j } C = \{T_0, T_j\} C={T0​,Tj​}, 且$T_j$作为新状态加入到状态转换矩阵的新行中
    • 若$T_j\in C$，跳过
    • 若$T_j=\varphi$，$T_j$不添加新行（原因：$T_j$属于无关状态中的死状态，具体见DFA的化简）

  • $(5)$记最后一个状态为$T_n$，对$T_0\sim T_n$进行状态重命名，并根据新状态名称重写状态转换矩阵，重写规则如下

    • 若$原初态X\in T_i$， $T_i$对应的新状态名就是新DFA的初态$S_0$
    • 若$原终态Y\in T_i$， $T_i$对应的新状态名加入新DFA的终态集合$Z$
    • 对矩阵中的所有$T_i$都重命名后，所得的状态转换矩阵就是确定化后的DFA状态矩阵
    • $I$表示当前状态s，$I_a$表示输入字母为$a$，矩阵$M[s,i]$的值就是状态s下输入a的次态o

  • $(6)$根据新状态转换矩阵画状态转换图，此时的状态转换图就是确定化之后的DFA图（未化简）

• 例题 ppt3.3-35（书p50 ex3.3 书图×，看ppt图）、 ppt3.3-37
  【gif动图–NFA的确定化】

DFA的化简

综合题型 & 课后习题

• 给出文法求DFA（求NFA–>转DFA–>DFA化简）
• NFA与正规式的互换

---

1. 3型文法 ↩︎ ↩︎

2. 左线性文法的状态转换图表示 ↩︎

3. ()、|、*、·四种运算运算规则 ↩︎

4. 正规式等价&正规式等价变换 ↩︎

5. 以01结尾的二进制数串：$(0|1{)}^{\ast }01$ ↩︎

6. 能被5整除的十进制整数：$(1|2|3|4|5|6|7|8|9)(0|1|2|3|4|5|6|7|8|9{)}^{\ast }(0|5)$ ↩︎

7. 包含奇数个1或奇数个0的二进制数串：$(1^{\ast }0)(1^{\ast }|01^{\ast }0)|(0^{\ast }1)(0^{\ast }|10^{\ast }1)$。解释：奇数个0与奇数个1的正规式类似，以求奇数个0为例，。。。。 ↩︎

8. 英文字母组成的所有符号串，要求符号串中的字母按照字典序排列：以a~z为例：$a^{\ast }{b}^{\ast }{c}^{\ast }...z^{\ast }$ ↩︎

9. 答案： ↩︎