在实际应用程序中涉及的线性表的基本操作都需要针对线性表的具体存储结构加以实现。线性表可以有两种存储表示方法:顺序存储表示和链式存储表示。下面我们先说说顺序存储表示。

1、顺序表——线性表的顺序存储表示

在计算机中表示线性表的最简单的方法是用一组地址连续的存储单元依次存储线性表的数据元素。换句话说,将线性表中的数据元素一个挨着一个地存放在某个存储区域中称线性表的这种存储方式为线性表的顺序存储表示。相应地,把采用这种存储结构的线性表称为顺序线性表,简称顺序表。

由于程序设计语言中的一维数组在内存中占据的也是一个地址连续的存储区域，因此可以用一维数组来描述顺序表中数据元素的存储区域。同时，由于线性表的长度可变。因此在顺序表的结构定义中,还需要设立一个表示线性表当前长度的域,并且因为线性表所需容量随问题不同而异，则还应该考虑数组容量可以进行动态扩充。

2、顺序表中基本操作的实现

容易看出,当线性表以上述定义的顺序表表示时,某些操作很容易实现。例如求线性表的长度和取得线性表中第i个数据元素等,因为线性表的长度是顺序表的一个“属性”,又第i个数据元素即为数组中第 i-1 个分量的值。因此,我们只讨论顺序表的其他几个主要操作的实现算法。

1.初始化操作

即构造一个空的顺序表。首先要按需为其动态分配一个存储区域,然后设其当前长度为 0。动态分配线性表的存储区域可以更有效地利用系统的资源,当不需要该线性表时可以使用销毁操作及时释放掉占用的存储空间。顺序表允许的最大容量maxsize 和需要扩容时的增量 incresize 大小可由用户设定,也可以不设定而采用系统规定的“默认值”。具体程序如下所示：

2.查找元素操作

要在顺序表 L 中查找其值与给定值 e 相等的数据元素,最简单的方法是,从第一个元素起,依次和 e 相比较,直至找到一个其值与 e 相等的数据元素,则返回它在线性表中的“位序”;或者查遍整个顺序表都没有找到其值和 相等的元素后返回“0”。在描述查找过程的程序中,设置了一个指示“位序”的整型变量 i 和指向顺序表中第 i 个元素存储位置的“指针”p。具体程序如下所示：

3.插入元素操作

假设有一个顺序存储表示的线性表 L:
(5，8，12，18，25，30，37，46，51，89)
需要在其第 4 个和第 5 个元素之间(即在第 5 个元素之前插人一个数据元素 23。显然,要实现这个“插入”,首先需要将存储在数组 L.Elem 中第 10 个分量至第 5 个分量中的数据元素“依次向后移动一个位置”,然后将 23 插入到 L.elem[4] 中,如图 2.2 所示。

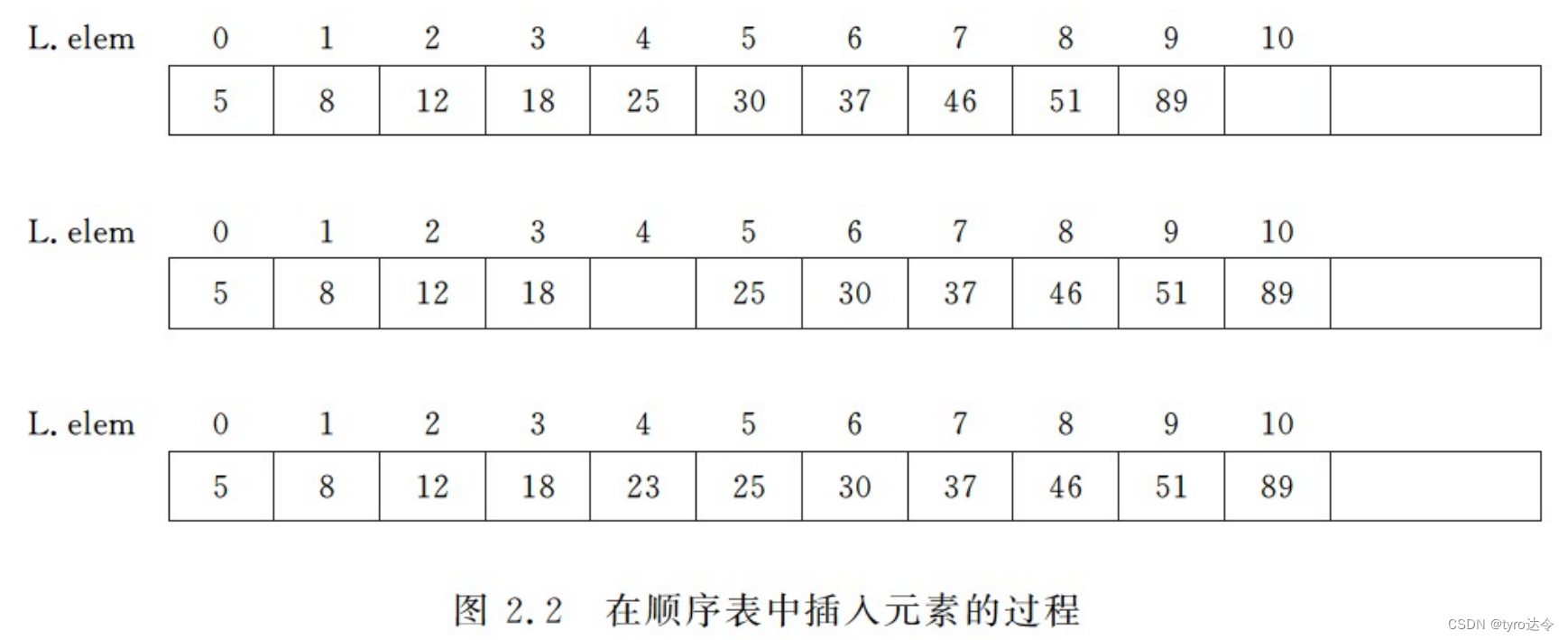
一般情况下,在顺序表 L 中第 i个元素之前插入一个新的元素时,首先需将L.elem[L.length-1]至 L.elem[i-1]依次向后移动一个位置。显然,此时顺序表的长度应该小于数组的最大容量;否则,在移动元素之前,必须先为顺序表“扩大数组容量”。具体程序如下所示：

其中，顺序表追加空间的函数为：

从算法中可见,一般情况下,当插入位置 i=L.length+1 时,for 循环的执行次数为 0,即不需要移动元素;反之,若 i=1,则需将表中全部( 个)元素依次向后移动。然而,当顺序表中数据元素已占满空间时,不论插入位置在何处,为了扩大当前的数组容量,都必须移动全部数据元素,因此,从最坏的情况考虑,顺序表插入算法的时间复杂度为 O(n),其中 n 为线性表的长度。容易看出，“扩容”的算法是很费时间的,特别是对当前表长较大的情况。因此在实际的应用程序中,应该尽量少用,也就是说,尽可能一次为顺序表分配足够使用的数组空间。

这其中有个自定义的错误处理函数ErrorMessage。该函数具体实现如下：

4.删除元素操作

假设需要从顺序存储表示的线性表 L:
(5，8，12，18，25，30，37，46，51，89)
中删除数据元素 25。为了使删除之后的线性表仍然保持顺序表的特点(元素“30”应该紧挨着元素“18”),必须将数组 L.elem 中从元素“30”至元素“89”依次向前移动一个位置,如图 2.3 所示。

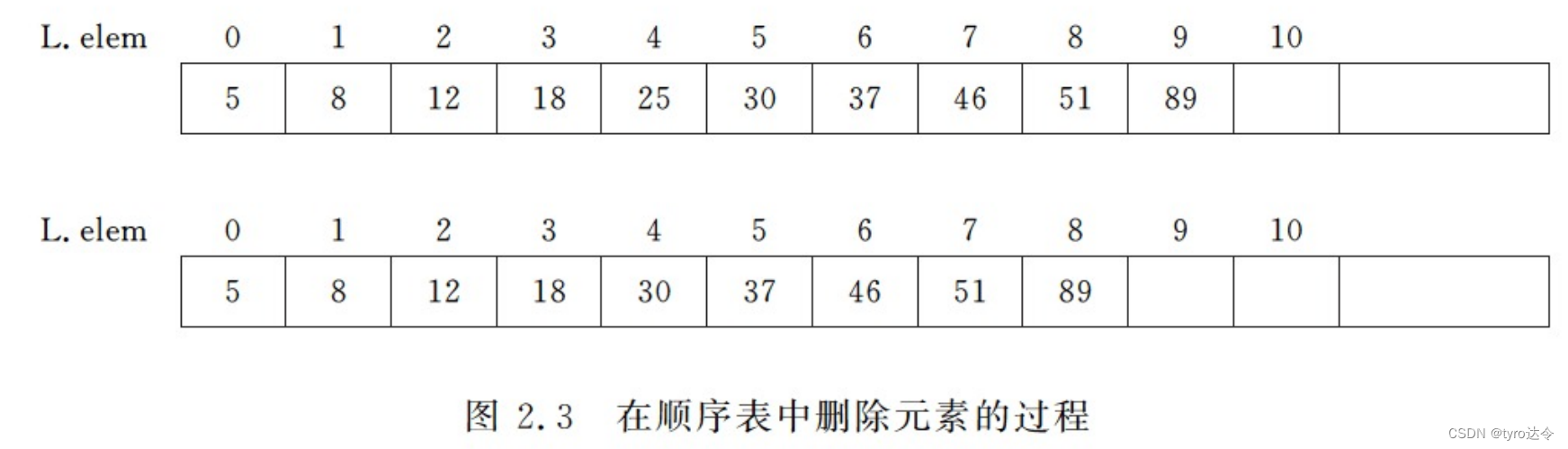
般情况下,从顺序表 L 中删除第个元素时,需将 L.elem [i- I]至L.elem[L.length-1]的元素依次向前移动一个位置。具体程序如下：

和插人的情况相类似，当删除位置i=L. length时,for循环的执行次数为0,即不需要移动元素;反之,若i=1,则需将顺序表中从第2个元素起至最后一个元素(共n-1个元素)依次向前移动一个位置。因此，顺序表删除元素算法的时间复杂度也为0(n),其中n为线性表的长度。

5.销毁结构操作

和结构创建相对应，当程序中的数据结构不再需要时,应该及时进行“销毁”,并释放它所占的全部空间，以便使存储空间得到充分的利用。具体程序如下：

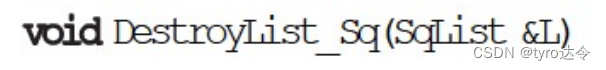
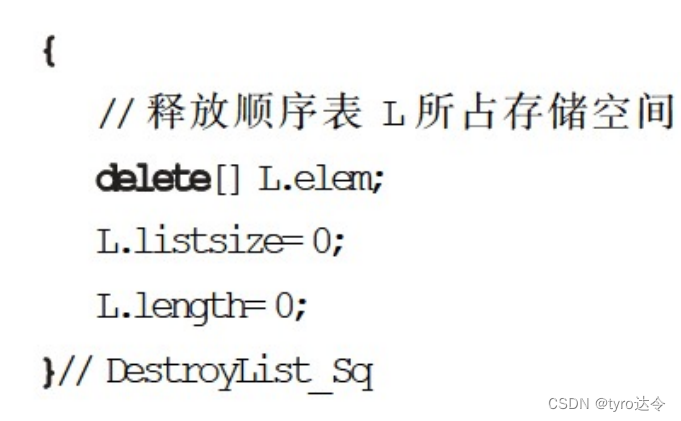
6.插入和删除操作的时间分析

从上述实现操作的算法中容易看出,在顺序表中插人或删除一个数据元素时,其时间主要消耗在移动元素上。并且,从描述移动的 for 循环语句中循环变量的上、下界看出,所需移动元素的个数和两个因素有关;其一是线性表的长度;其二是被插或被删元素在线性表中的位置。当元素被插入到线性表中最后一个元素之后或者被删除的是线性表中最后一个元素时,不需要移动顺序表中其他元素:反之,当元素被插入到线性表中第一个元素之前或者被删除的是线性表中第一个元素时,需要将顺序表中所有元素均向表尾或表头移动一个位置。由于插入和删除都可能在线性表的任何位置上进行,从统计意义上讲,考虑在顺序表的任一位置上进行插人或删除的“平均时间特性”更有实际意义。因此需要分析它们的平均性能,即分析在顺序表中任何一个合法位置上进行插入或删除操作时“需要移动元素个数的平均值”。

令 Ein(n)表示在长度为 n 的顺序表中进行一次插入操作时所需进行“移动”个数的期望值(即平均移动个数),则

其中,pi是在第i个元素之前插入一个元素的概率,n-i+1 是在第 个元素之前插人一个元素时所需移动的元素个数。由于可能插入的位置 i=1,2, … ,n+1 共 n+1个,假设在每个位置上进行插入的机会均等，则

由此,在上述等概率假设的情况下，

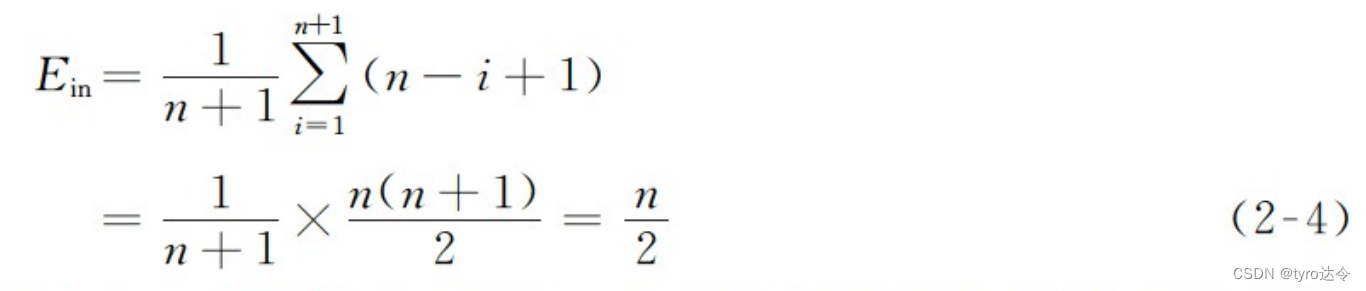
类似地,令 Edl(n)表示在长度为 n 的顺序表中进行一次删除操作时所需进行“移动”个数的期望值(即平均移动个数),则

其中,qi是删除第 i 个元素的概率,n-i 是删除第 i 个元素时所需移动元素的个数。同样假设在 n 个可能进行删除的位置 i=1,2, … ,n 机会均等,则

由此,在上述等概率的假设下，

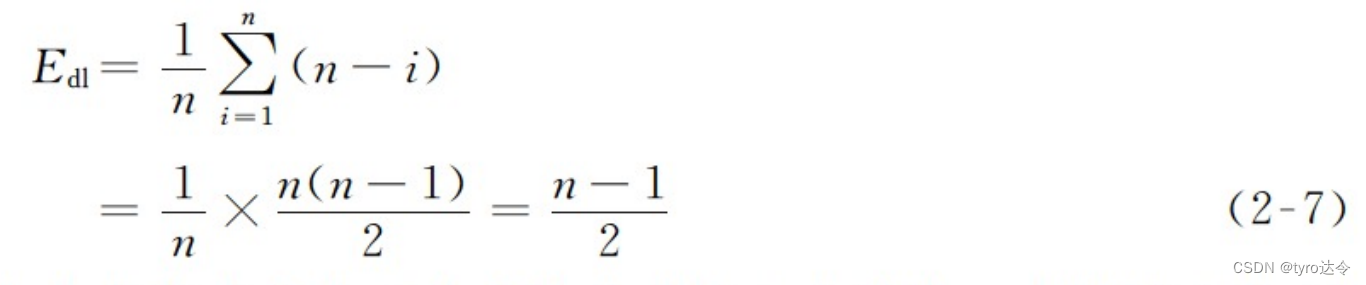
由式(2-4)和式(2-7)可见,在顺序存储表示的线性表中插入或删除一个数据元素,平均约需移动表中一半元素。这在线性表的长度较大时是很可观的。这个缺陷完全是由于顺序存储要求线性表的元素依次紧挨存放所造成的。因此,这种顺序存储表示仅适用于不经常进行插入和删除操作并且表中元素相对稳定的线性表。