T306713 Hello, 2023
题目背景
Goodbye, 2022
Hello, 2023
题目描述
某 E 在 2022 年的幸运数字是 x x x,这个数可能是正的,也可能是负的。
某 E 想要知道 x m o d 2023 x \bmod 2023 xmod2023 的值。其中, m o d \bmod mod 是取模操作。也就是说,你需要求出 x x x 除以 2023 2023 2023 的余数,这个余数必须是非负整数。
例如, 2022 m o d 2023 = 2022 2022 \bmod 2023 = 2022 2022mod2023=2022, 2025 m o d 2023 = 2 2025 \bmod 2023 = 2 2025mod2023=2, − 2 m o d 2023 = 2021 -2 \bmod 2023 = 2021 −2mod2023=2021, − 2026 m o d 2023 = 2020 -2026 \bmod 2023 = 2020 −2026mod2023=2020。
具体来说, x = k × 2023 + r x = k \times 2023 + r x=k×2023+r,其中 0 ≤ r < 2023 0 \le r < 2023 0≤r<2023, k , r k,r k,r 都是整数。你需要求出这个 r r r。
请注意:如果你使用 C/C++ 语言中的取模运算符( % \texttt{\%} %)对负数取模,你将会得到一个负数作为结果。在这个负数结果上加上模数,得到的才是正确的取模结果。
自己的思路:
利用取余符号来完成求模,输出题目中要求的r即可,但也要小心这个r在不同语言中得出的结果不同。(都是对2023的取余)
输入格式
输入一行一个整数 x x x。
输出格式
输出 x m o d 2023 x \bmod 2023 xmod2023 的值。
样例 #1
样例输入 #1
2022
样例输出 #1
2022
样例 #2
样例输入 #2
2025
样例输出 #2
2
样例 #3
样例输入 #3
-2
样例输出 #3
2021
样例 #4
样例输入 #4
-2026
样例输出 #4
2020
在这里插入代码片
铺地毯
题目背景
为了准备一个独特的颁奖典礼,组织者在会场的一片矩形区域铺上一些正方形地毯。
题目描述
这片矩形区域长 a a a 米,宽 b b b 米。地毯为边长为 c c c 米的正方形。
他想要知道,在地毯不进行裁切且两两不重叠的前提下,能否使用若干张这种地毯铺满整个矩形,如果可以铺满,那么铺满整个矩形需要多少张地毯。
输入格式
输入共一行,为三个正整数 a , b , c a, b, c a,b,c,分别表示矩形区域的长、宽和地毯的边长。
输出格式
输出共一行。
如果无法使用若干张这种地毯铺满整个矩形,输出一行一个 -1。
如果可以使用若干张这种地毯铺满整个矩形,输出一行一个正整数,代表铺满整个矩形需要的地毯的数量。
样例 #1
样例输入 #1
20 15 5
样例输出 #1
12
样例 #2
样例输入 #2
39 17 24
样例输出 #2
-1
提示
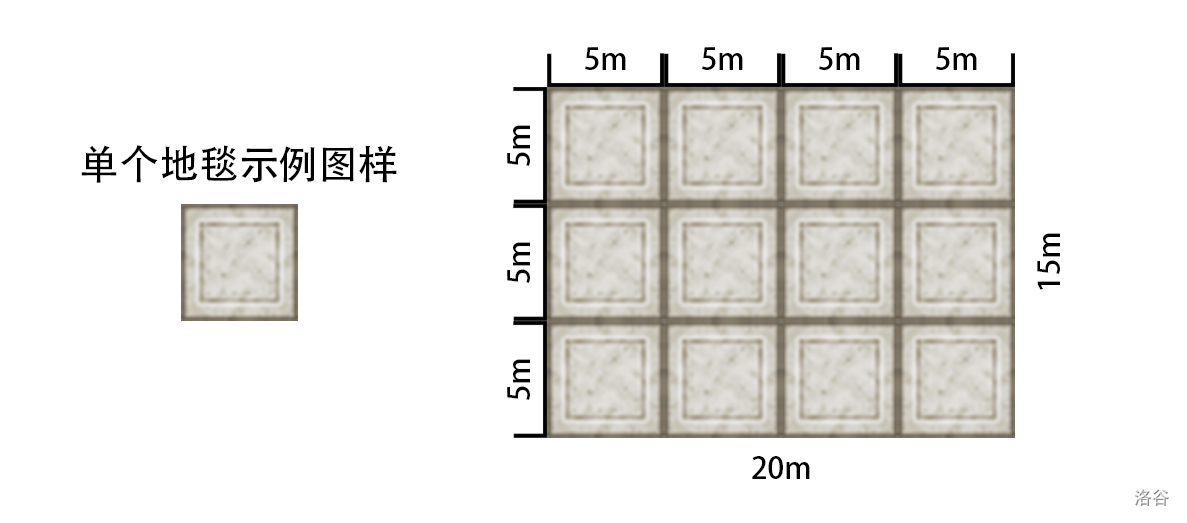
样例 1 解释
将地毯按如下方式放置 12 12 12 张即可铺满整个矩形。
样例 2 解释
容易发现,不存在任何一种方式可以使用若干张此类地毯铺满整个矩形。
数据规模与约定
对于所有测试点: 1 ≤ a , b ≤ 1 0 18 1 \leq a, b \leq 10 ^ {18} 1≤a,b≤1018, 1 ≤ c ≤ 1 0 18 1 \leq c \leq 10 ^ {18} 1≤c≤1018。保证如果存在答案,最终答案不超过 1 0 18 10 ^ {18} 1018。
| 测试点 | a , b a, b a,b | c c c | 特殊性质 |
|---|---|---|---|
| 1 , 2 1, 2 1,2 | ≤ 1 0 3 \leq 10 ^ 3 ≤103 | ≤ 1 0 3 \leq 10 ^ 3 ≤103 | 无 |
| 3 , 4 3, 4 3,4 | ≤ 1 0 18 \leq 10 ^ {18} ≤1018 | = 1 = 1 =1 | 无 |
| 5 5 5 | ≤ 1 0 18 \leq 10 ^ {18} ≤1018 | ≤ 1 0 18 \leq 10 ^ {18} ≤1018 | 保证 a , b < c a, b < c a,b<c |
| 6 ∼ 10 6 \sim 10 6∼10 | ≤ 1 0 18 \leq 10 ^ {18} ≤1018 | ≤ 1 0 18 \leq 10 ^ {18} ≤1018 | 无 |
思考
前两个输入的数据(长和宽)对输入的第三个数据进行取余,由样例分析可知,不管是长还是宽都必须满足这前面两个数对第三个数的取余不能为0才能满足条件。(而且必须是两个取余都为0时,且前面输入的两个数长和宽不能小于后面输入的第三个数) 直接判断不行,输出-1就行。
一次函数
题目描述
在二维平面坐标系 x O y xOy xOy 中,一个点的位置可以由横坐标 x x x 和纵坐标 y y y 两个参数描述,其坐标记为 ( x , y ) (x,y) (x,y)。
一次函数 y = k x + b y=kx+b y=kx+b 是满足纵坐标 y y y 等于 k k k 乘以纵坐标 x x x 加 b b b 的点的集合,即满足该条件的点都在该一次函数的直线上。
现在有 n n n 个点,第 i i i 个点的坐标为 ( x i , y i ) (x_i,y_i) (xi,yi)。
现在请你求出,分别有多少点,在给定的一次函数图像上。
形式化地,给出 n n n 对整数 ( x , y ) (x,y) (x,y),请你求出有多少对数满足 y = k × x + b y=k\times x+b y=k×x+b。
输入格式
输入共 n + 1 n+1 n+1 行。
输入的第一行为三个整数 n , k , b n,k,b n,k,b。
接下来 n n n 行,每行两个数 x i , y i x_i,y_i xi,yi,代表第 i i i 个点的坐标。
输出格式
输出一行一个整数,代表有多少点在给出的一次函数上(即满足 y i = k x i + b y_i = kx_i+b yi=kxi+b)。
样例 #1
样例输入 #1
5 3 0
0 0
1 3
2 7
3 9
-1 -4
样例输出 #1
3
提示
样例 1 解释
给出的一次函数为 y = 3 x y=3x y=3x。
点 ( 0 , 0 ) (0,0) (0,0), ( 1 , 3 ) (1,3) (1,3), ( 3 , 9 ) (3,9) (3,9) 在一次函数上,共 3 3 3 个。
数据点性质
对于
30
%
30\%
30% 的测试点,
n
=
1
n=1
n=1;
对于
100
%
100\%
100% 的测试点,
1
≤
n
≤
1
0
6
1 \le n \le 10^6
1≤n≤106,
0
≤
∣
k
∣
,
∣
b
∣
≤
1
0
5
0 \le |k|,|b| \le 10^5
0≤∣k∣,∣b∣≤105,
0
≤
∣
x
i
∣
,
∣
y
i
∣
≤
1
0
9
0 \le |x_i|,|y_i| \le 10^9
0≤∣xi∣,∣yi∣≤109。