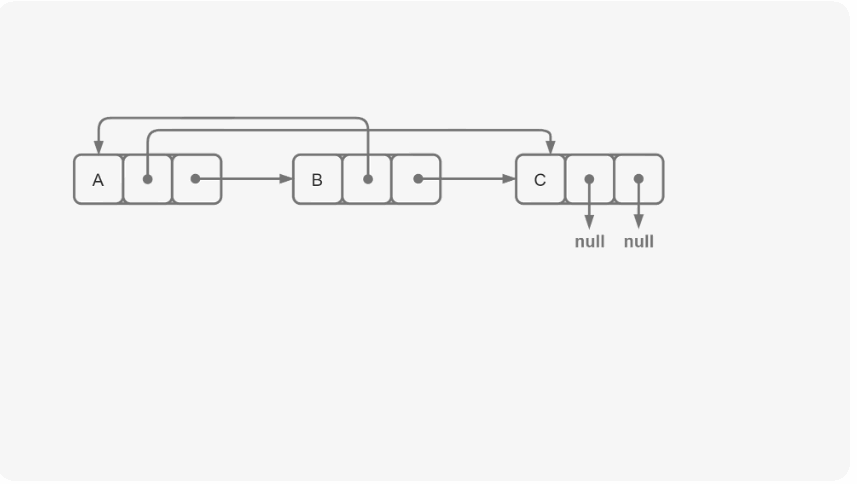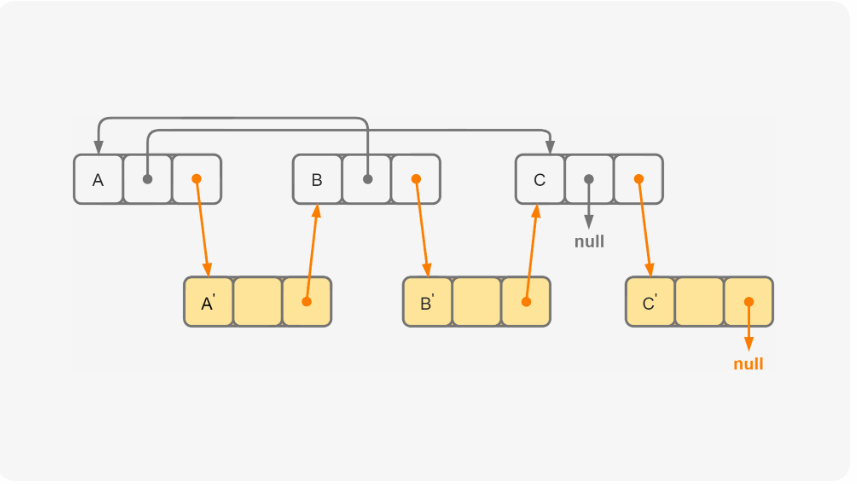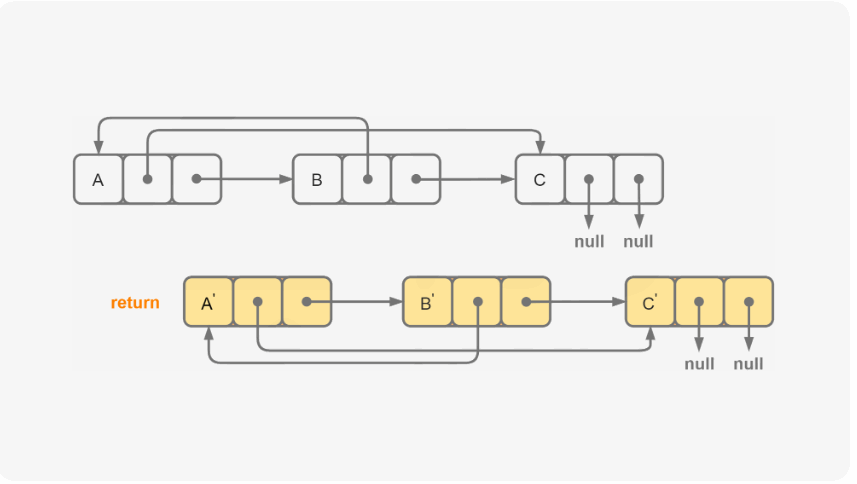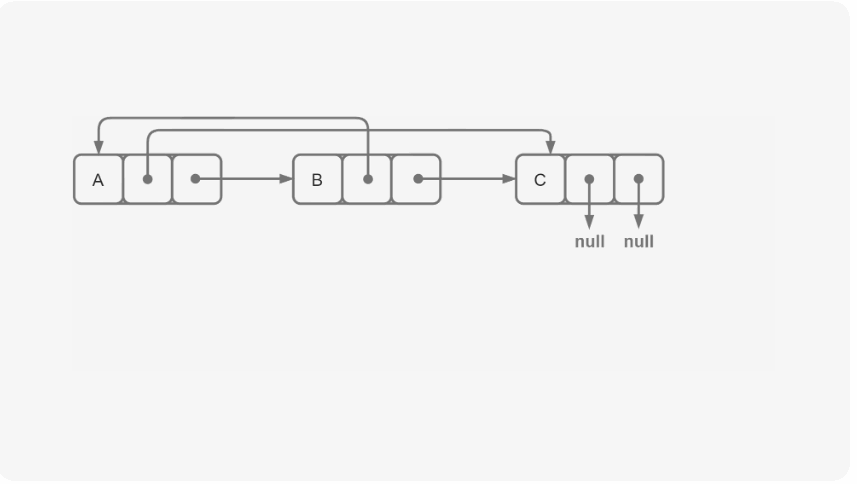
思路：

首先使用递归来解，从0开始到N，每次都从index开始到N的求出最大值。然后再次递归index+1到N的最大值，再求max。代码如下：

  // 方法一：使用递归方式找出最大乘积
    public static int maxProduct(int[] nums) {
        // 检查输入的数组是否为空
        if (nums == null || nums.length == 0) {
            return 0;
        }
        int N = nums.length;
        // 从数组的第一个元素开始递归处理
        return process(nums, 0, N);
    }

    // 辅助递归函数
    private static int process(int[] nums, int index, int N) {
        // 递归的终止条件：当处理到数组的最后一个元素时，返回该元素
        if (index == N - 1) {
            return nums[index];
        }
        int max = nums[index]; // 当前位置的最大乘积初始化为当前元素
        int cur = nums[index]; // 当前乘积
        // 计算从index开始所有可能的子数组乘积
        for (int i = index + 1; i < N; i++) {
            cur = cur * nums[i];
            max = Math.max(max, cur);
        }
        // 返回当前计算的最大值与递归调用下一个元素的结果的最大值
        return Math.max(max, process(nums, index + 1, N));
    }

第二种方法：

使用动态规划

public static int maxProduct(int[] nums) {
        // 检查输入数组是否为空
        if (nums == null || nums.length == 0) {
            return 0;
        }
        int N = nums.length;
        int[] dp = new int[N + 1]; // 创建DP数组
        dp[N] = Integer.MIN_VALUE; // 初始化边界条件
        dp[N - 1] = nums[N - 1]; // 最后一个元素的最大乘积是其自身
        // 从后向前遍历数组
        for (int index = N - 1; index >= 0; index--) {
            int cur = nums[index];
            dp[index] = Math.max(cur, dp[index + 1]);
            for (int i = index + 1; i < N; i++) {
                cur = cur * nums[i];
                dp[index] = Math.max(dp[index], cur);
            }
        }
        return dp[0]; // 返回整个数组的最大子数组乘积
    }

第三种方法 一次for循环，代码如下：

    // 方法三：优化的动态规划解法（一次遍历）
    public static int maxProduct(int[] nums) {
        // 检查数组是否为空
        if (nums == null || nums.length == 0) {
            return 0;
        }

        int max = nums[0], min = nums[0], result = nums[0]; // 初始化最大值、最小值和结果

        // 遍历数组元素
        for (int i = 1; i < nums.length; i++) {
            // 如果当前数是负数，交换最大值和最小值
            if (nums[i] < 0) {
                int temp = max;
                max = min;
                min = temp;
            }

            // 更新到当前位置的最大值和最小值
            max = Math.max(nums[i], max * nums[i]);
            min = Math.min(nums[i], min * nums[i]);

            // 更新全局最大乘积结果
            result = Math.max(result, max);
        }

        return result; // 返回结果
    }