使用栈来模拟一个队列，要求实现队列的两个基本操作:入队、出队。

栈的特点：先入后出，出入元素都是在同一端（栈顶）。

 

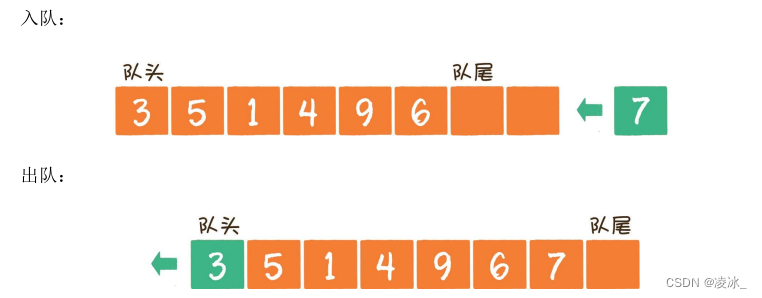
队列的特点：先入先出，出入元素是在两端（队头和队尾)。 

 

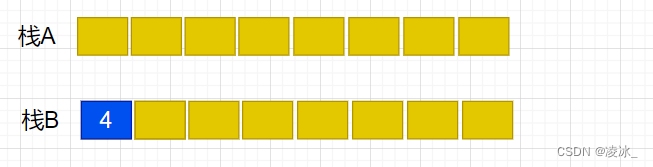
分析：我们需要A，B两个栈，A栈为队列入口，负责插入新元素，B栈为队列出口，负责移除老元素。 

 

图解所示：

（1）元素3入队

 （2）元素5入队

 （3）元素1入队 

 

    让栈A中的所有元素按顺序出栈，再按照出栈顺序压入栈B。这样一来，元素从栈A弹出并压入栈B的顺序是1、5、3，和当初进入栈A的顺序3、5、1是相反的。

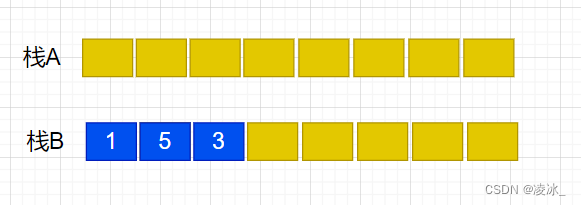
 （4） 元素3出队 

（5） 元素5出队  

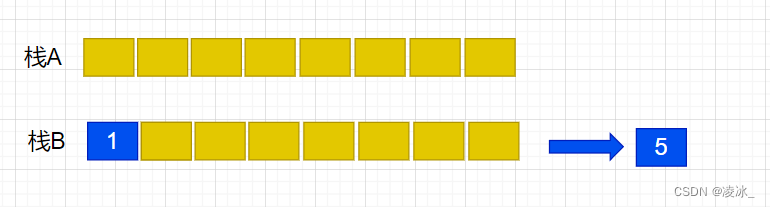  （6）元素4入队  

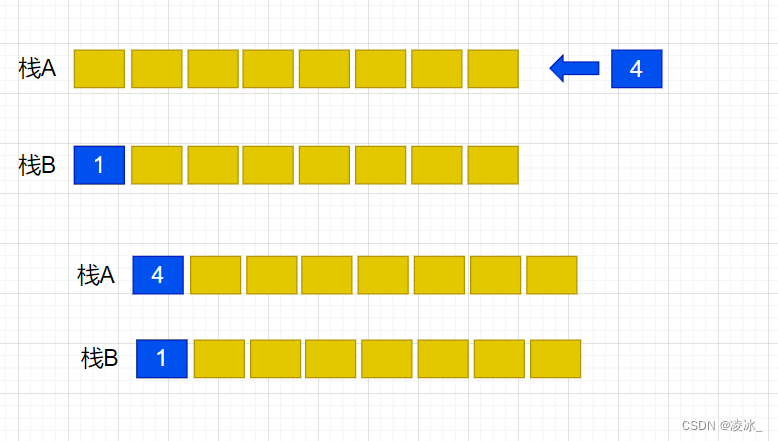 （7） 元素1出队  

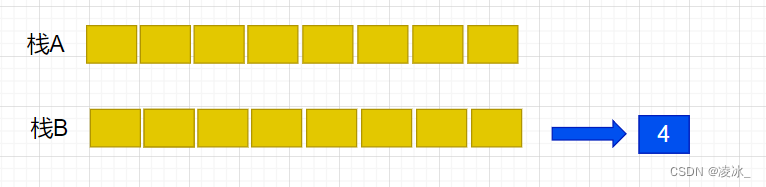
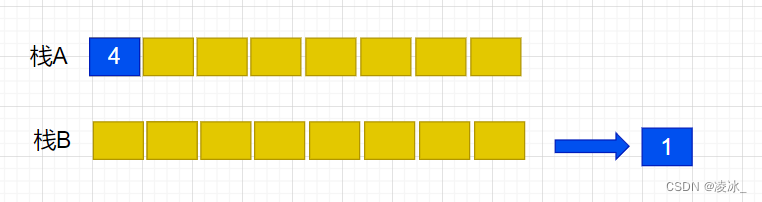 （8）  元素4出队  

class StackToQueue:
    def __init__(self):
        self.sak_A=[]
        self.sak_B=[]
    #入队
    def in_queue(self,element):
        self.sak_A.append(element)

   #栈A出队的压入栈B
    def to_trans(self):
        #循环栈A大于0，则添加到栈B中的是（栈A出队的元素）
        while len(self.sak_A)>0:
            self.sak_B.append(self.sak_A.pop())
    #出队
    def de_queue(self):
        if len(self.sak_B)==0:
            if len(self.sak_A)==0:
                raise Exception('栈已空了！')
            self.to_trans() #调用方法
        return self.sak_B.pop()  #栈B出队

if __name__ == '__main__':
    sq=StackToQueue()
    sq.in_queue(3)
    sq.in_queue(5)
    sq.in_queue(1)
    #出队
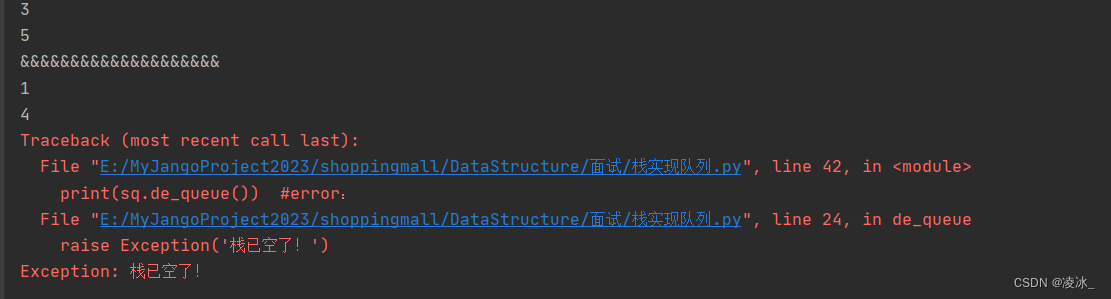
    print(sq.de_queue())  #3
    print(sq.de_queue())  #5
    print("&"*20)
    #入队
    sq.in_queue(4)
    # 出队
    print(sq.de_queue())  #1
    print(sq.de_queue())  #4
    # print(sq.de_queue())  # 发生异常

     总之：入队操作的时间复杂度显然是O (1)。至于出队操作，如果涉及栈A和栈B的元 素迁移，那么一次出队的时间复杂度是o (n)﹔如果不用迁移，时间复杂度是O(1)。所以把时间均摊到每一次出队操作上面，其时间复杂度是O （1)