判断链表中是否有环

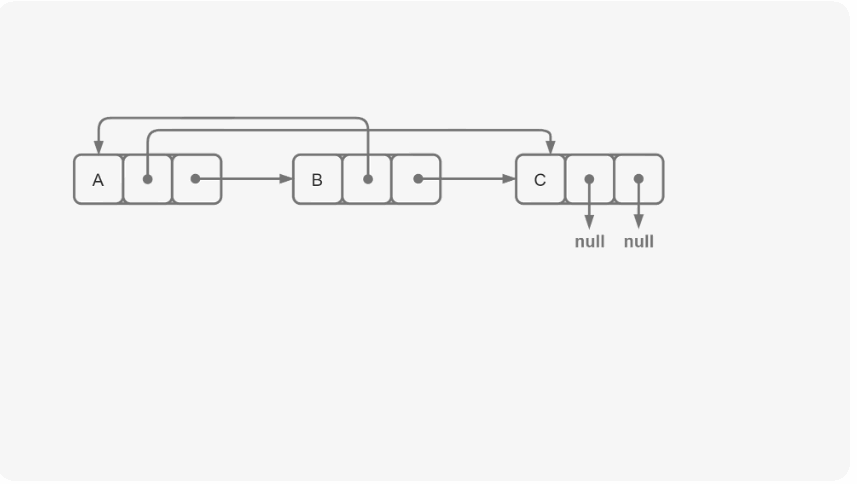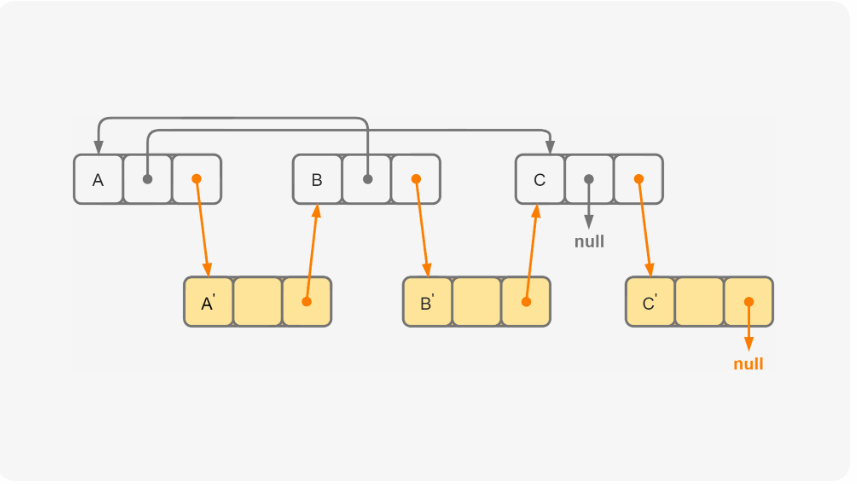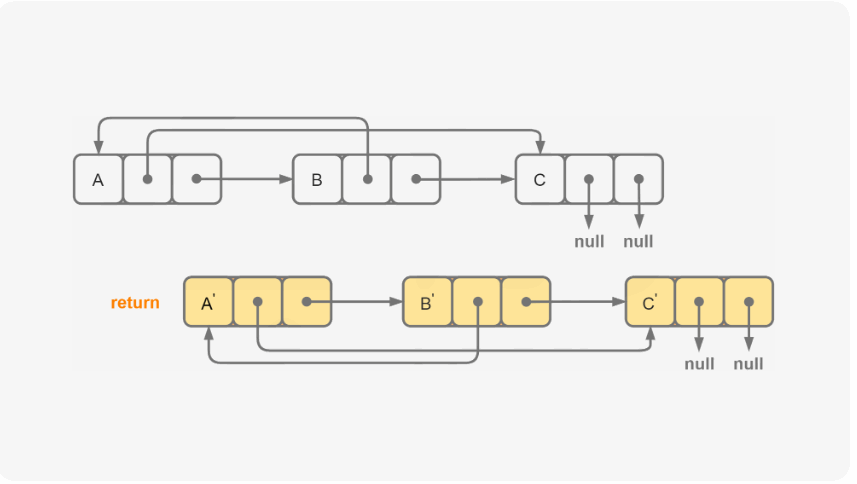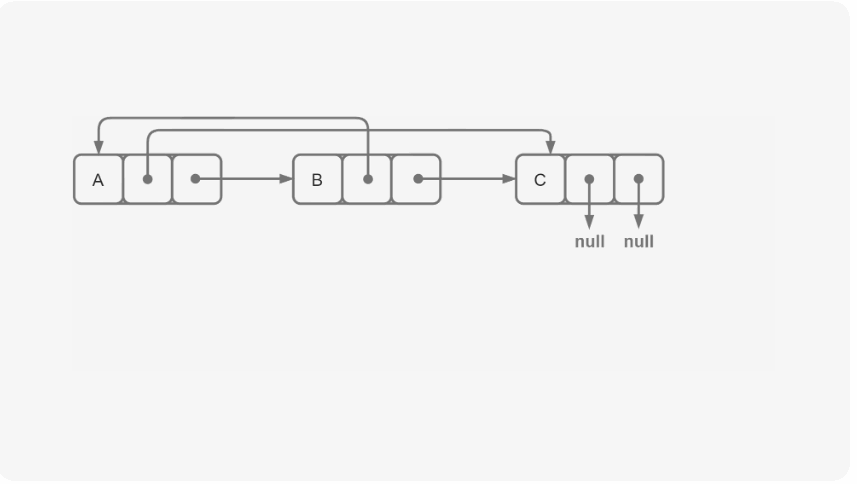
题目：给你一个链表的头节点 head ，判断链表中是否有环。
解决方法：使用快慢指针
如果两个快慢指针相遇，则有环。
如果没有相遇，则没有环。

但是这个原理是什么呢？
原理：当慢指针走到圆环的第一个节点，这时快指针已经进入到了圆环当中，慢指针走一步，快指针走两步，假设慢指针走到圆环当中的第一个节点时，慢指针和快指针相差N步

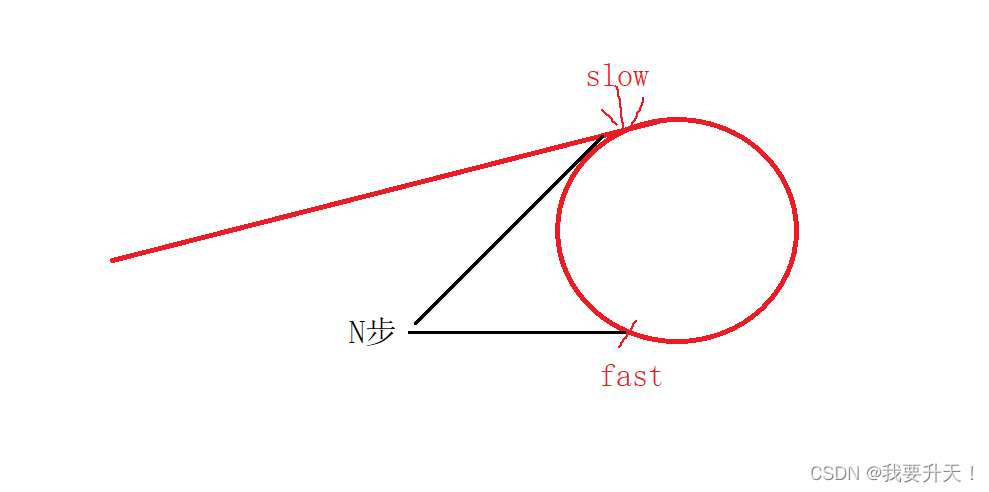
慢指针走一步，快指针走两步，那么快指针和慢指针之间相差的步数就是N+1-2 = N-1；

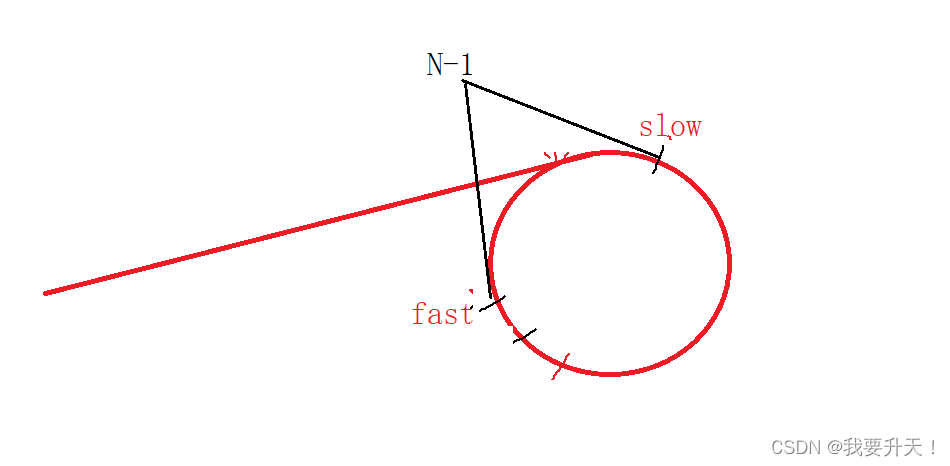
以此类推 N，N-1，N-2......0，每追击一次，距离减少1，距离为0，则表示追到了。
因此，慢指针和快指针会相遇,此时链表就是一个环形链表。

bool hasCycle(struct ListNode* head) {
    struct ListNode* slow = head;
    struct ListNode* fast = head;
    while (fast && fast->next) {
       slow = slow->next;
        fast = fast->next->next;
        if (slow == fast) {
            return true;
        }
        
    }
    return false;
}

快慢指针步数问题

那么请问，如果慢指针走一步，快指针走3步、4步、n步，也可以判断链表是否带环吗？请证明
1.情况1：慢指针走1步，快指针走3步
按照刚才的分析方法，我们可以知道慢指针走一步，快指针走3步，那么快指针和慢指针之间相差的步数就是N+1-3 = N-2；

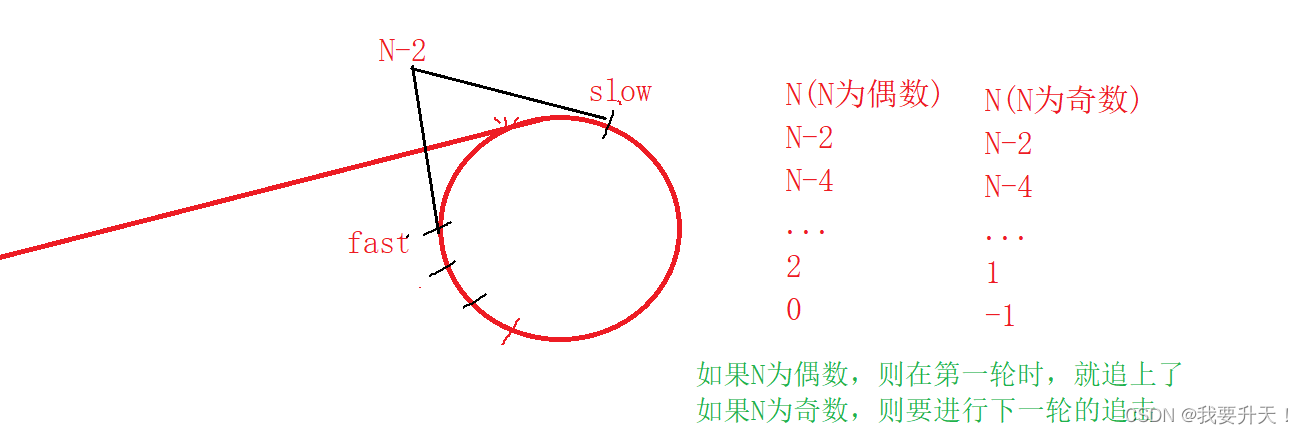
如果N为偶数，则在第一轮时，就追上了。
如果N为奇数时，则要进行下一轮的追击。
假设环的长度为C,那么当N为奇数时，开始下一次的追击时，距离为-1的情况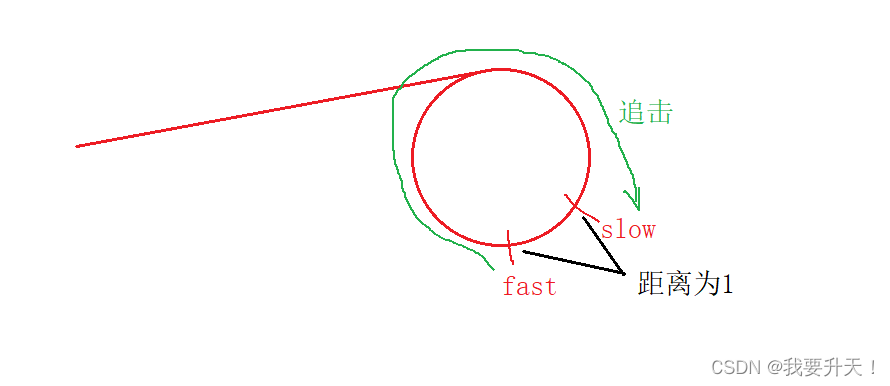
但是，如果C是偶数，则C-1是奇数，又会造成N是奇数，就会一直追击，则追不上。
如果C是奇数，则C-1是偶数，N就是偶数，在追击一轮就可追击成功。
因此，如果存在以下这种情况，那么就无法追击成功
“N为奇数，C为偶数同时存在”

但是，这种情况真的会存在吗？我们接下来讨论一下
假设头节点为head,慢指针为slow,快指针为fast
头指针到圆环的第一个节点的距离是L,此时慢指针也在圆环的第一个节点，快指针已经进入到了圆环内。

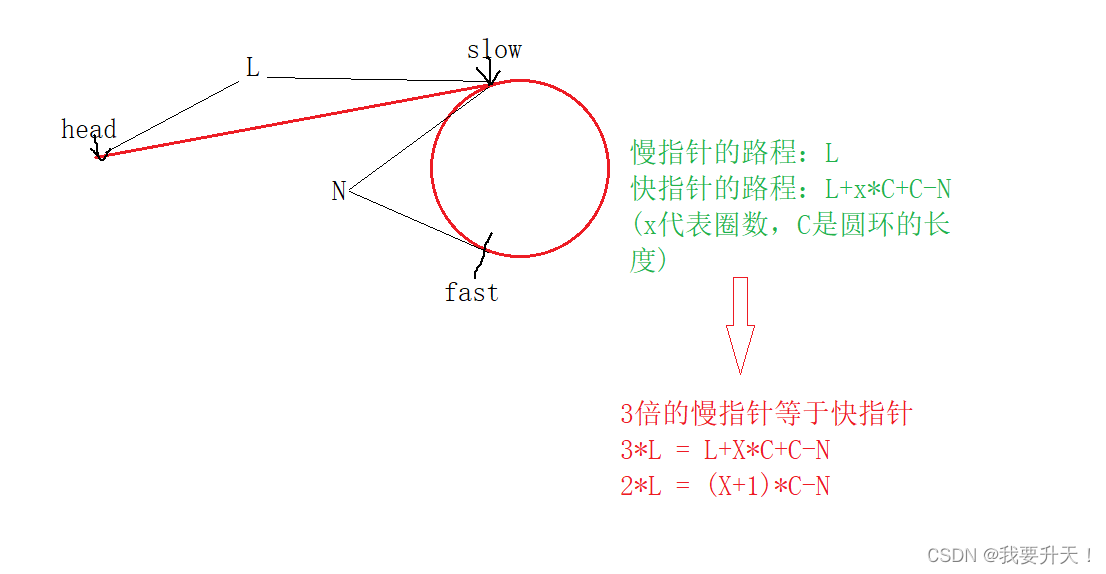
2*L的结果一定是偶数，如果N是奇数的话，那么C也必须是奇数，等式才会成立，偶数 = 奇数-奇数
如果·N是偶数的话，那么C也必须是偶数，等式才会成立，偶数=偶数-偶数
这两个条件都不满足
“N为奇数，C为偶数同时存在”
因此，当慢指针走一步，快指针走3步，不会被追击上的条件不成立，因此，当慢指针走一步，快指针走3步时，一定会被追击上。
2，情况2：慢指针走一步，快指针走4步
依旧按照上面的方法，我们可以知道慢指针走一步，快指针走4步，那么快指针和慢指针之间相差的步数就是N+1-4 = N-3；


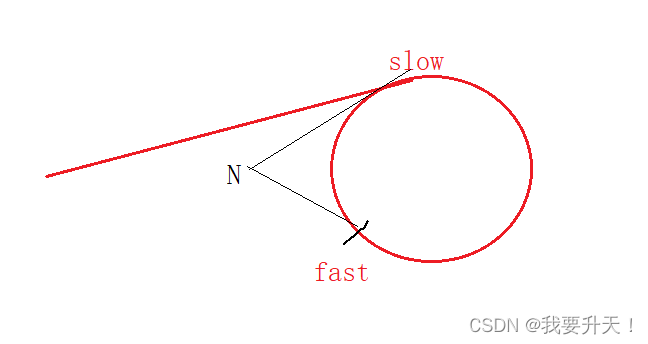
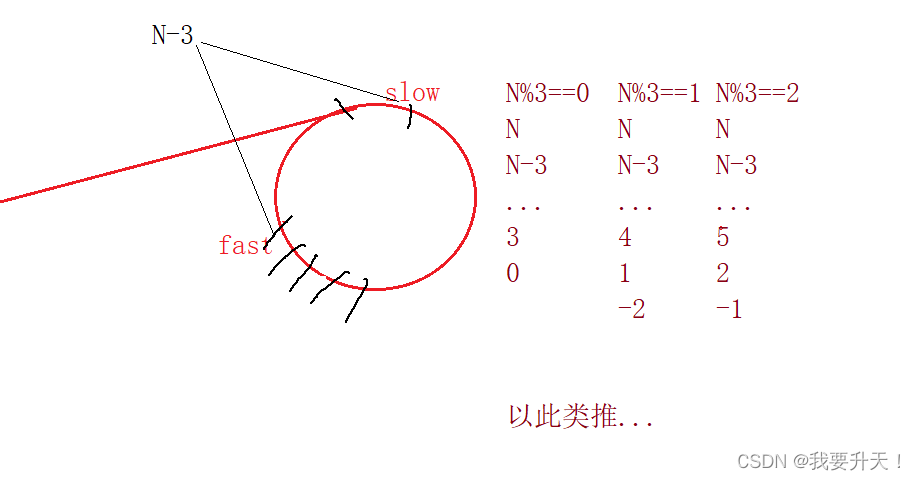
这样之后，我们就要去讨论C的取值了,C-2,C-1…