引言：本篇博客详细讲解了关于链表的三个经典例题，分别是：环形链表（简单），环形链表Ⅱ（中等），随机链表的复制（中等）。当你能毫无压力地听懂和成功地写出代码时，那就一定可以充分的证明你的链表知识学习地非常扎实了！

更多有关C语言的知识详解可前往个人主页：计信猫

目录

一，环形链表（简单）

1，题目描述

2，思路分析

3，代码解答

 二，环形链表（简单）的拓展

1，提出问题

2，问题Ⅰ的解答

3，问题Ⅱ的解答

4，问题Ⅱ中C与N的关系

三，环形链表 Ⅱ（中等）

1，题目描述

2，思路分析

3，代码解答

四，随机链表的复制（中等）

1，题目描述

2，思路分析

3，代码解答

五，结语

---

一，环形链表（简单）

1，题目描述

OJ链接：环形链表

       给你一个链表，判断链表中是否存在环，若存在，则返回true，反之，则返回false。

2，思路分析

        为了解出这道题，我们可以使用一个在链表中可谓是大名鼎鼎的方法——快慢指针。

        所谓的快慢指针就是定义两个结构体指针slow和fast，而fast指针每次比slow指针多走一步。假如我们将fast比作兔子，slow比作乌龟。

        那么显而易见，假如整个链表里边没有环，则兔子（fast指针）一定会先走到NULL；假如整个链表里边有环，则兔子（fast指针）一定会先进入环，并一直在环里边循环着走，一直到乌龟（slow指针）进入环，由于兔子和乌龟具有速度差，所以在某一时间刻乌龟和兔子一定会相遇，所以如果兔子和乌龟相遇了，即链表有环。

3，代码解答

if(head==NULL)//判断链表是否为空
        {
            return false;
        }
        struct ListNode*fast=head->next;//定义快指针
        struct ListNode*slow=head;//定义慢指针
        while(fast&&fast->next)
        {
            if(fast==slow)//两指针相遇，则成环
            {
                return true;
            }
            fast=fast->next->next;//快指针每次走两步
            slow=slow->next;//慢指针每次走一步
        }
        return false;

 二，环形链表（简单）的拓展

1，提出问题

假如你正在参加某个hr的面试，而面试官刚刚好问到你这个问题，经过充分准备的你毫不费力地将这道题秒杀了。但面试官接下来又提出了两个问题：

1，为什么fast和slow指针一定会相遇，请给出证明

2，当fast指针一次走n步时，快慢指针还会不会相遇？

这时候，阁下又该如何是好呢？

2，问题Ⅰ的解答

        其实遇到这种问题我们完全没必要慌张，我们只需要拿出作为程序员严谨的态度给予证明就可以了。

        我们可以假设在fast和slow都进入环的时候，两指针的间距为N。既然每进行一次追击，fast都前进两步，slow前进一步，那么它们之间的距离一定会缩小一步。

那么当我们进行了N次追击，则间距则会如此变化：N，N-1，N-2……1，0。

        所以如此来看，两指针的间距一定会变为0，那么fast和slow指针也一定会相遇！（第一关通过，获得50%的offer）

3，问题Ⅱ的解答

        此时对于n的具体取值我们就需要分开讨论了，我们就先以n等于3来进行讨论吧！

我们设进入环的时候两指针的间距d等于N，故每一次追击之后d=N-（n-1）=N-2，再设整个环的长度为C。

   

         当d为偶数时，距离每次减少2，则可以追上。

        但当d为奇数时，就要另当别论了：

d为奇数时，第一次的追击则会错过：N，N-2，N-4……1，-1。而这里的-1意味着fast指针会跑到slow指针的前一位去，并开始新一轮的追击。

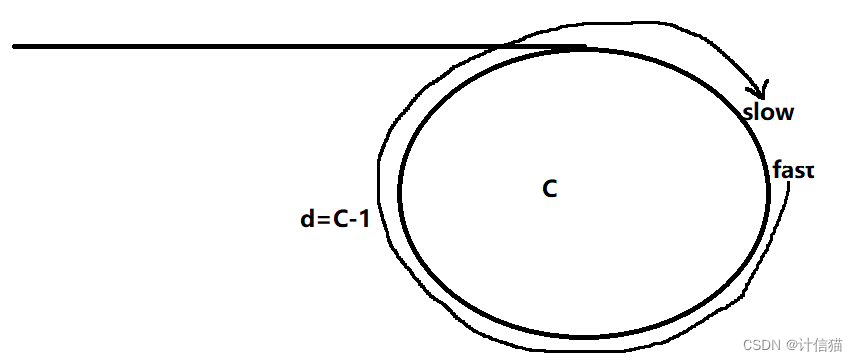
        那么此时我们就需要再次讨论d=C-1的奇偶关系了。

当C为奇数时，d=C-1为偶数，则可以追上。
当C为偶数时，d=C-1为奇数，则又会进入下一次追击，进入死循环，永远也追不上

         所以其他n的取值情况也就同样方法继续思考了。（第二关通过，获得100%的offer)

4，问题Ⅱ中C与N的关系

        看了上面问题Ⅱ的解析后，我们都知道了快慢指针是否可以相遇与C，N的奇偶性相关。而C与N之间是否有存在着奇偶性的关系呢？答案是肯定的。

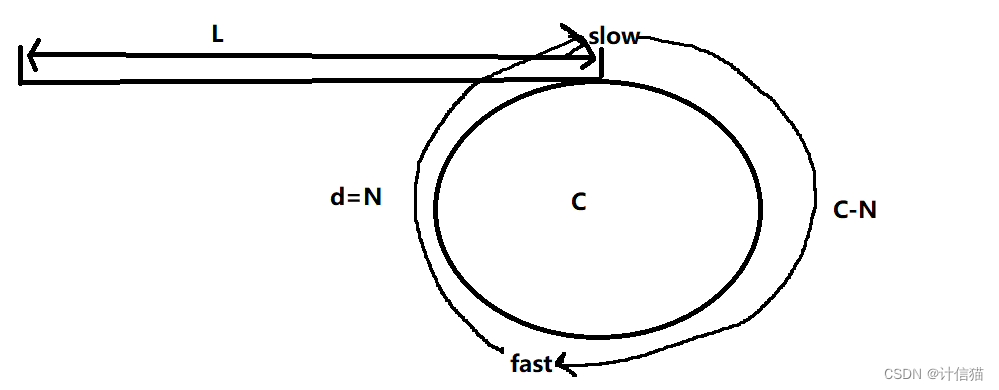
我们还是以n=3来进行分析，假设进环之前的路程长度为L，当slow进入环的时候，fast已经在环里边走了x圈。

而此时slow和fast指针走的路程分别如下：

        因为n=3，那么此时fast走的路程就是slow走的路程的三倍，所以我们可以得到等式：

3*L=L+x*C+C-N

        那么进行等式化简之后，我们便可以得到：

2*L=（x+1）*C-N

        所以在问题Ⅱ中，若d=N为奇数，C为偶数的条件一定是不存在的！！原因如下：

三，环形链表 Ⅱ（中等）

1，题目描述

OJ链接：环形链表Ⅱ

        这次的不一样的地方就是需要在普通环形链表的基础上返回链表成环的节点。

2，思路分析

        关于这道题，我将会介绍一个十分巧妙的方法：一个指针从链表的头节点head开始出发，另一个指针从fast和slow指针相遇的节点meet出发，最终它们一定会在成环的起始节点相遇。

证明：

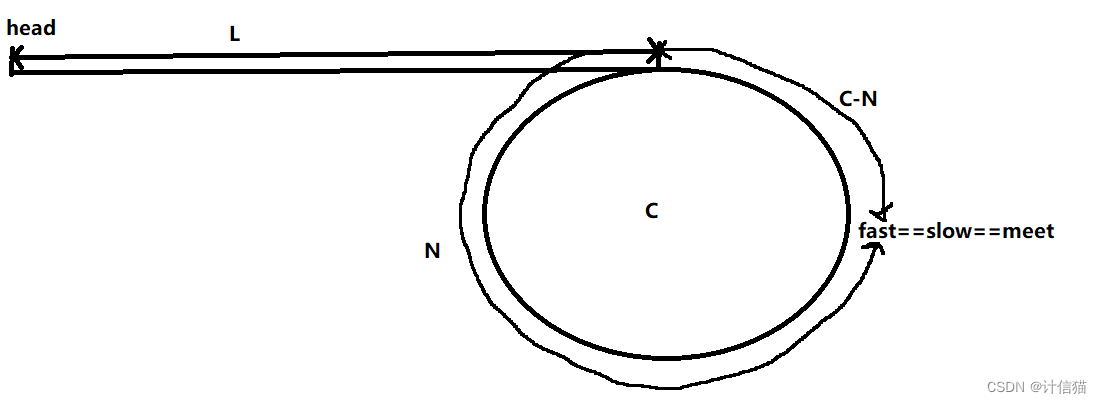
还是老样子，我们假设在fast和slow相遇的时候，fast已经走了x圈。

那么此时slow和fast走的路程分别为：

        所以我们便可以得到如下等式：

2（L+N）=L+x*C+N     =>    L=x*C-N

         故等号左边的L就表示第一个指针从头节点head到成环起始节点的距离，等号右边的x*C不就相当于是周期吗，并没有影响，剩下的N不就表示着meet节点到成环起始节点的距离吗？所以等号左右两边相等，以上方法成立！

3，代码解答

struct ListNode *detectCycle(struct ListNode *head) 
{
    struct ListNode*fast=head;
    struct ListNode*slow=head;
    //寻找meet节点
    while(fast&&fast->next)    
    {
        slow=slow->next;
        fast=fast->next->next;
        if(slow==fast)
        {
            struct ListNode*meet=slow;//找到meet节点
            struct ListNode*cur=head;//使用cur从头节点出发
            while(meet!=cur)
            {
                cur=cur->next;
                meet=meet->next;
            }
            return meet;//cur和meet相遇的节点则为成环起始节点
        }
    }
    return NULL;
}

四，随机链表的复制（中等）

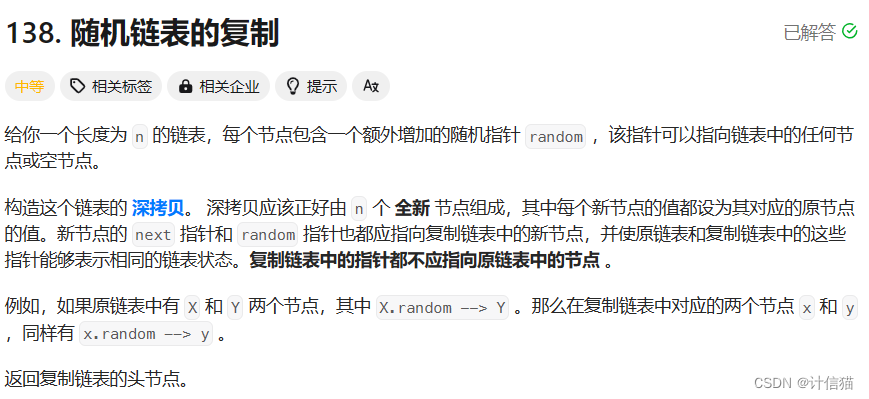
1，题目描述

OJ链接：随机链表的复制

        给定你一个链表，链表中含有一个随即指针random，它指向链表的其他节点或者NULL，如下：

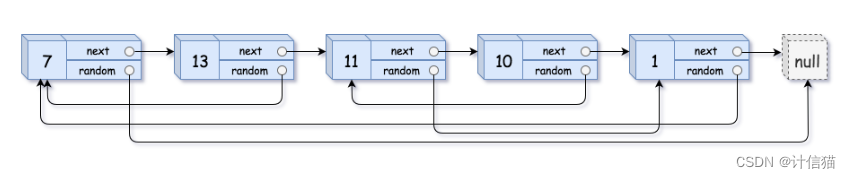         而你需要做的就是复制一个与原链表一模一样的链表，并且与对原链表毫无影响。

2，思路分析

        其实这道题本身不难，复制一个链表简直易如反掌，而唯一的难点就是这个结构体成员random指针。它导致了复制random时，可能链表的那个random节点还没出现的问题。

         但是我们可以以以下方式解决问题：

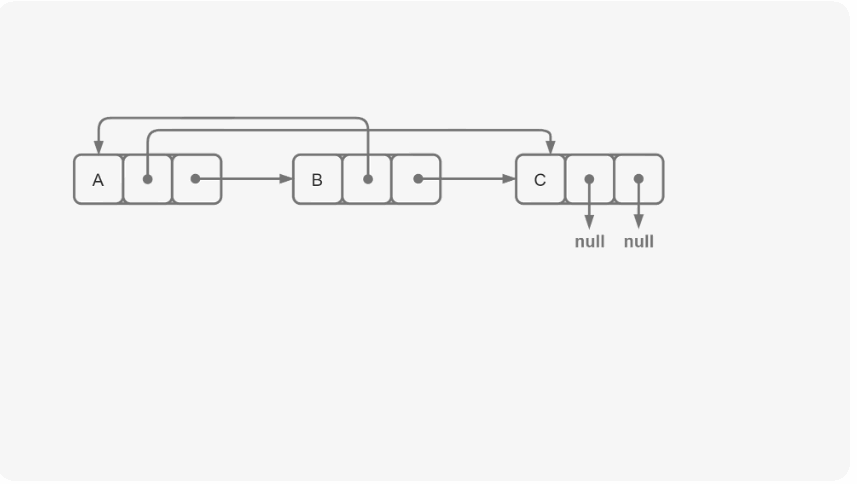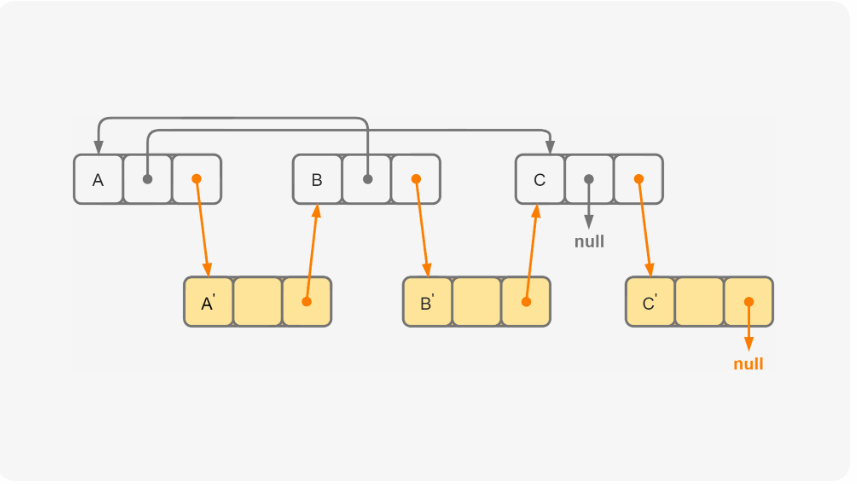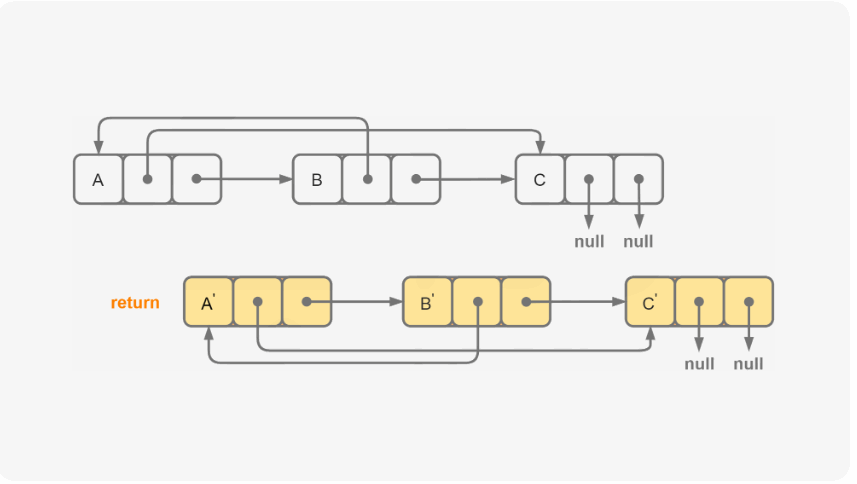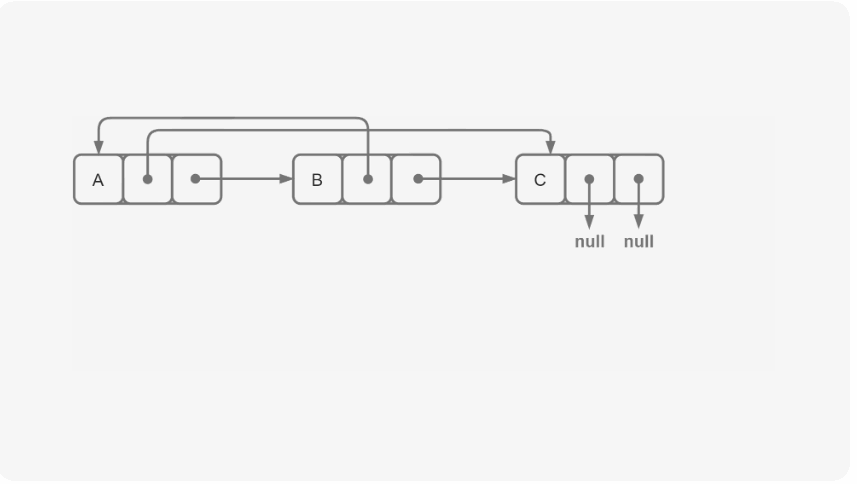
        如上所示，我们可以先在每一个原链表节点之后插入一个与原节点一模一样的节点（先不管random指针），然后我们再对插入节点的random指针赋值，最后再将插入的指针取下来就可以了。

        可能很多人会问道，random指针如何赋值呢？其实很简单，当我们将节点插入之后，random指针的值不就是原指针random所指向的值的next吗？这样，random的赋值就完美的解决了！ 

3，代码解答

struct Node* BuyNode(int val)//设计一个创建节点的函数
{
    struct Node*newnode=(struct Node*)malloc(sizeof(struct Node));
    newnode->next=NULL;
    newnode->val=val;
    return newnode;
}
struct Node* copyRandomList(struct Node* head)
{
//防止空链表
    if(head==NULL)
    {
        return NULL;
    }
   //创建后继节点
   struct Node*cur=head;
   while(cur)
   {
        struct Node*newnode=BuyNode(cur->val);
        newnode->next=cur->next;
        cur->next=newnode;
        cur=cur->next->next;
   }
   //赋值random
   struct Node*newcur=head;
   struct Node*follow=newcur->next;
   while(follow)
   {
    if(newcur->random==NULL)//random指向NULL就特殊处理赋值NULL
    {
        follow->random=NULL;
        //指针遍历链表的移动
        newcur=newcur->next->next;
        if(follow->next)
        {
            follow=follow->next->next;
        }
        else
        {
            break;
        }
    }
    else
    {
        follow->random=newcur->random->next;
        //指针遍历链表的移动
        newcur=newcur->next->next;
        if(follow->next)
        {
            follow=follow->next->next;
        }
        else
        {
            break;
        }
    }
        
   }
   //将后继结点分离
   struct Node*phead=head->next;
   struct Node*ptail=head->next;
   while(ptail->next)
   {
        ptail->next=ptail->next->next;
        ptail=ptail->next;
   }
   return phead;
}

五，结语

        其实这些题讲起来看起来非常轻松，但也耗费了我不少时间去做出它（甚至还是在看了题解的前提下）。

        但让我值得欣慰的是，我还是结合题解做出了这些题，甚至第二题我还自己想出来自己的方法，而且我也十分顺利的在博客里清楚的讲解出了每道题的做法。这也证明了我的链表学习还是取得了效果。

        希望我的这篇博客也可以同样帮助到热爱编程学习的你，让我们一起进步一起加油！！