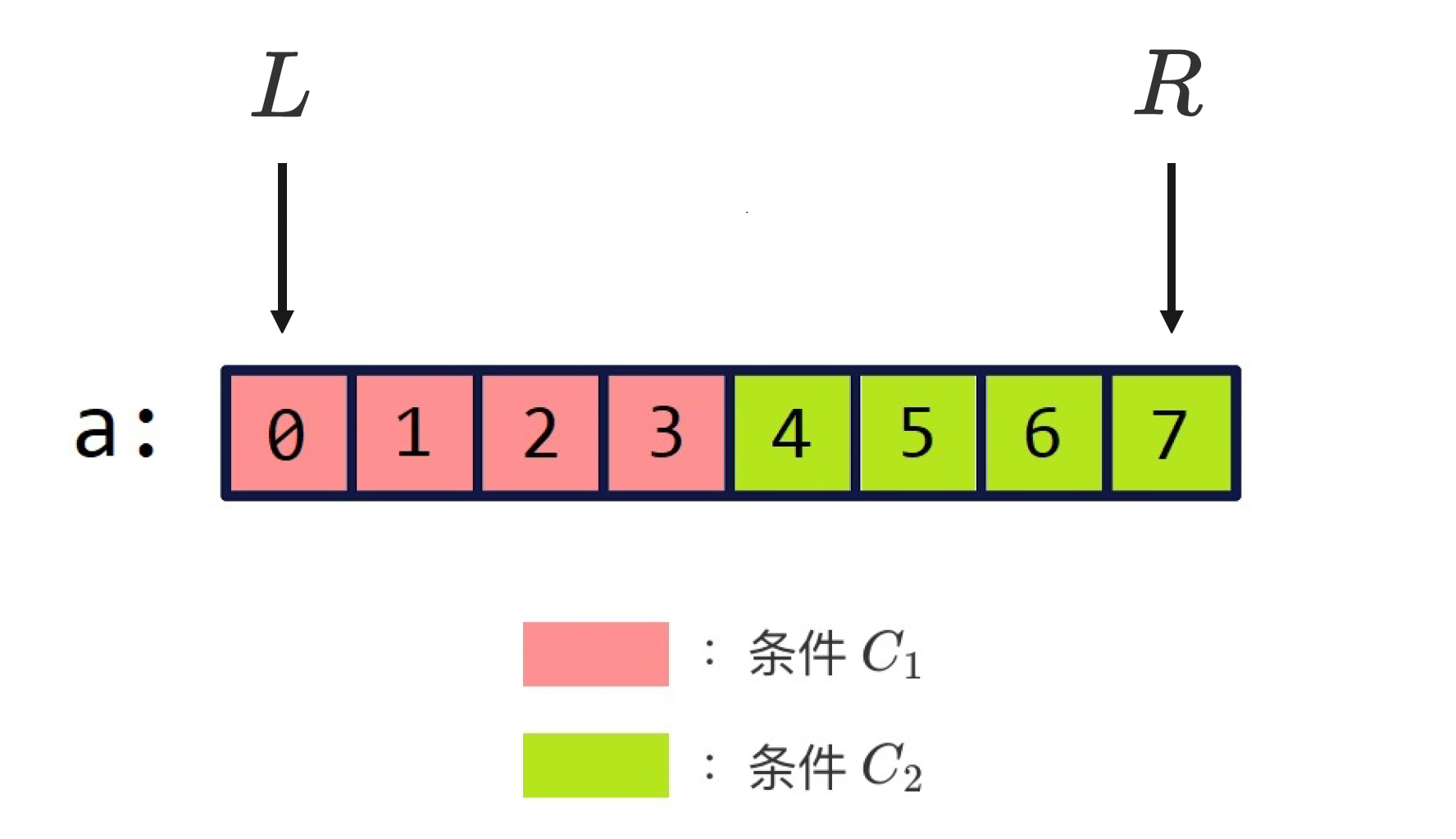
什么是差分

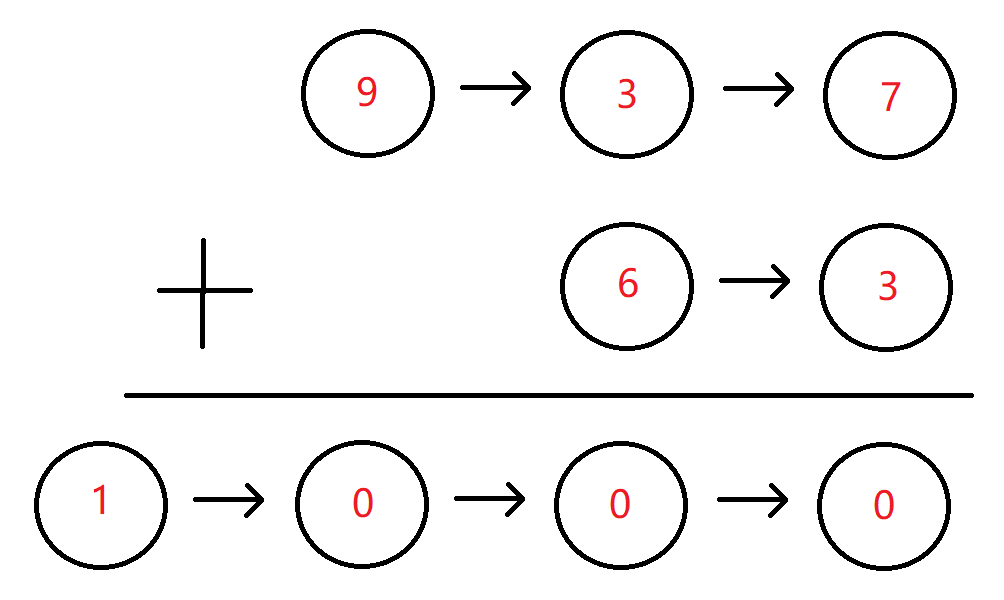
对于一个数组a：a1,a2,a3...an

我们构造一个数组b：b1,b2,b3...bn

使得数组a是数组b的前缀和数组，即ai = b1 + b2 ... + bi

则数组b就是数组a的差分

差分有什么用

当我们得到数组b后，只用对b求一遍前缀和，就能得到数组a，耗时O(n)

假设有如下需求：给一个范围[l,r]，对数组a，在这个范围内的数全部加上c

如果暴力做，需要每次都耗时O(r-l)

但如果用差分做，每次只用耗时O(1)，最后再对差分数组求一个前缀和得到原数组

那具体怎么用差分做呢？

我们看看给一个范围[l,r]，对数组a，在这个范围内的数全部加上c，对数组b有什么影响

首先，需要对b[l]加上c，这样a[l]就加上了c，a[l+1]也加上了c，一直到a后面所有的数

为什么a[l,…]的数都相当于加上了c？因为数组a是数组b的前缀和，即ai = b1 + b2 … + bi，一旦b[i]加上c，a[i]和后面的数都会加上c

但我们只让a[l,r]范围内的数加上c，a[r+1]及以后的数不能加上c，因此需要打个补丁，让b[r+1]减去c

因此，如果想对数组a在区间[l,r]范围内都加上c，只用对其差分数组b修改两个数即可：

• b[l] += c
• b[r+1] -= c

private static void insert(int[] b,int l,int r,int c){
    b[l] += c;
    b[r+1] -= c;
}

怎么初始化差分数组

刚才的前提是，对于原始数组a，假设已经有个对应的差分数组，怎么进行后续的操作

那怎么根据原始数组a初始化一个差分数组呢？

我们可以看做对一个数据都为0的数组，进行了n次插入操作：

• 第一次将a[0,0]范围内增加a[0]
• 第一次将a[1,1]范围内增加a[1]
• 依此类推

代码如下：

private static int[] genDiff(int[] a) {
    int n = a.length;
    int[] b = new int[n+1];
    for (int i = 0;i<n;i++){
        insert(b,i,i,a[i]);
    }
    return b;
}

怎么根据差分数组得到原始数组

根据定义，如果数组b是数组a的差分，则数组a是数组b的前缀和

因此对数组b求一遍前缀和，就能得到原始数组，即得到数次范围内的数都增加的结果：

a[0] = b[0];
for (int i = 1;i<n;i++){
    a[i] = a[i-1] + b[i];
}

什么是二维差分

一维差分是针对一个一维数组，快速对这个数组的某一段区间内的所有数都增一个值的结构

二维差分类似，就是在一个二维数组中，快速对某个矩形范围内的数都增加一个值的结构

如果暴力做法，每次都需要遍历将目标矩形中的所有数都加上一个值，时间复杂度较高

如果用二维差分做，每次只用耗时O(1)

定义：

• 原始数组a
• 差分数组b

a中的每个元素为b中的二维前缀和，即a[i][j] 的值为 在b中，以b[0][0]为左上角，以b[i][j]为右下角的矩形中所有元素的和

例如：要对元素数组a中以4个角为 (x1,y1) (x1,y2) (x2,y1) (x2,y2) 的矩形内的所有元素都加上c：

首先在差分数组b中，给b[x1][y1]加上c：

根据二维前缀和的定义，这样相当于给所有a中，在(x1,y1)下边和右边的所有点都加上了c，即数组a中的右下部分区域

但其实只用对目标区域加上c，而对于图中的R1，R2，R3这3个区域不需要加上c，需要进行补偿操作：

• b[x2+1,y1] -= c：相当于给a中R2，R3区域都减去c
• b[x1,y2+1] -= c：相当于给a中R1，R3区域都减去c

可以发现R3区域多减了个c，因此还需要进行补偿：

• b[x2+1,y2+1] += c：相当于给a中R3区域都加上c

这样，每次对原始数组a中某个矩形区域加上c，只用操作差分数组b中的4个位置即可，时间复杂度大大降低

private static void insert(int[][] arr,int x1,int y1,int x2,int y2,int c){
    arr[x1][y1] += c;
    arr[x2+1][y1] -= c;
    arr[x1][y2+1] -= c;
    arr[x2+1][y2+1] += c;
}

如何初始化二维差分数组

和一维差分数组的初始化类似，当我们拿到原始数组a后，遍历数组a中的每个元素a[i][j]

按照对以只有该元素的矩形（即左上角a[i][j]，右下角a[i][j]的矩形）增加a[i][j]操作即可：

// 差分数组
int[][] diff = new int[n+1][m+1];
for (int i = 0;i<n;i++){
    for (int j = 0;j<m;j++){
        insert(diff,i,j,i,j,arr[i][j]);
    }
}