C++之set/map相关实现

news2025/1/9 15:18:20

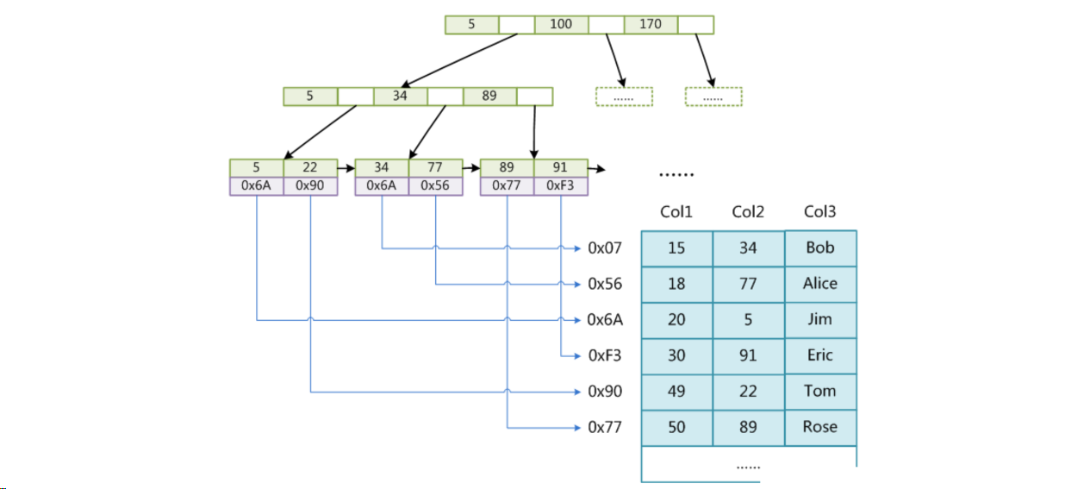
看着上面的图片，你可能对set和map的多样变化产生疑惑，下面我们就来详细讲解他们的区别以及实现

一.set/map

首先，在这里我们要声明，如果你对二叉搜索树一点都不了解的话，建议你先去将搜索二叉树学会再来学习这里的内容！！！

我也实现过一个二叉搜索树的内容，如下，仅供参考：

数据结构之搜素二叉树-CSDN博客

如果你了解过一些map/set的内容可能会知道，其实实现其是有两种方法的，注意：如果你连map和set是什么都不知道的话，建议Reference - C++ Reference

对于AVLTree实现和红黑树实现，STL中使用红黑树实现的，但是我们两种数据结构都会进行一定的讲解：

AVLTree实现：

#pragma once


template<class K,class V>
struct AVLTreeNode
{
	//构造函数
	AVLTreeNode(const pair<K,V>& kv)
		:_left(nullptr),_right(nullptr),_parent(nullptr),_bf(0),_kv(kv)
	{}
	//成员变量
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;
	int _bf;
	pair<K,V> _kv;
};
template<class K,class V>
class AVLTree
{
	typedef AVLTreeNode<K, V> Node;
public:
	bool insert(const pair<K, V>& kv)
	{
		//两步骤：
		//1.按照搜索二叉树规则插入
		//特殊
		if (_root == nullptr)
		{
			_root = new Node(kv);
			return true;
		}
		Node* root = _root;
		Node* parent = nullptr;
		while (root)
		{
			//注意：比较的是第一个元素
			if (root->_kv.first < kv.first)
			{
				parent = root;
				root = root->_right;				
			}
			else if (root->_kv.first > kv.first)
			{
				parent = root;
				root = root->_left;
			}
			else
			{
				return false;
			}
		}
		//通过parent来确定插入位置
		root = new Node(kv);
		if (parent->_kv.first < kv.first)//右边
		{
			parent->_right = root;
		}
		else
		{
			parent->_left = root;
		}
		root->_parent = parent;
		//步骤二：根据平衡因子来修改AVL树
		while (parent)
		{
			if (root == parent->_left)
				parent->_bf--;
			else
				parent->_bf++;
			//检查bf
			if (parent->_bf == 0)
			{
				break;
			}
			else if (parent->_bf == 1 || parent->_bf == -1)
			{
				//说明要处理上面
				root = root->_parent;
				parent = parent->_parent;
			}
			else if (parent->_bf == 2 || parent->_bf == -2)
			{
				//旋转处理
				//左单旋
				if (parent->_bf == 2 && root->_bf == 1)
				{
					RotateL(parent);
				}
				//右单旋
				else if (parent->_bf == -2 && root->_bf == -1)
				{
					RotateR(parent);
				}
				//左右双旋
				else if (parent->_bf==-2 && root->_bf == 1 )
				{
					RotateLR(parent);
				}
				//右左双旋
				else if (parent->_bf == 2 && root->_bf == -1)
				{
					RotateRL(parent);
				}
				else
				{
					return false;
				}
				break;//注意点
			}
			else
			{
				//出现其他情况，说明AVL树有问题
				return false;
			}
		}
		return true;
	}
	int height()
	{
		return _height(_root);
	}
	//序遍历
	//中序遍历
	void Preorder() 
	{
		_Preorder(_root);
	}
	void Inorder()
	{
		_Inorder(_root);
	}
	void Postorder()
	{
		_Postorder(_root);
	}
	size_t size()
	{
		return _size(_root);
	}
	Node* find(const K& key)
	{
		Node* cur = _root;
		while (cur)
		{
			if (cur->_kv.first < key)
			{
				cur = cur->_left;
			}
			else if (cur->_kv.first > key)
			{
				cur = cur->_right;
			}
			else
			{
				return cur;
			}
		}
		return nullptr;
	}
	bool balance()
	{
		int height = 0;
		return _balance(_root, height);
	}
private:
	bool _balance(Node* root, int& height)
	{
		if (root == nullptr)
		{
			height = 0;
			return true;
		}
		int leftheight = 0, rightheight = 0;
		//三查
		if (!_balance(root->_left, leftheight) || !_balance(root->_right, rightheight))
		{
			return false;
		}
		if (abs(rightheight - leftheight) >= 2)
		{
			cout << root->_kv.first << "不平衡" << endl;
			return false;
		}
		if (rightheight - leftheight != root->_bf)
		{
			cout << root->_kv.first << "平衡因子异常" << endl;
			return false;
		}
		//重置height
		height = max(leftheight, rightheight) + 1;
		return true;
	}
	size_t _size(Node* root)
	{
		if (root == nullptr)
			return 0;
		return _size(root->_left) + _size(root->_right) + 1;
	}
	int _height(Node* root)
	{
		if (root == nullptr)
			return 0;
		int leftsub = _height(root->_left);
		int rightsub = _height(root->_right);
		return max(leftsub, rightsub) + 1;
	}
	void _Preorder(Node* root)
	{
		if (root == nullptr)
			return;
		cout << root->_kv.first << " " << root->_bf << endl;
		_Inorder(root->_left);
		_Inorder(root->_right);
	}
	void _Inorder(Node* root)
	{
		if (root == nullptr)
			return;
		_Inorder(root->_left);
		cout << root->_kv.first << " " << root->_bf << endl;
		_Inorder(root->_right);
	}
	void _Postorder(Node* root)
	{
		if (root == nullptr)
			return;
		_Inorder(root->_left);
		_Inorder(root->_right);
		cout << root->_kv.first << " " << root->_bf << endl;
	}
	//旋转操作:
	void RotateL(Node* parent)
	{
		//保留四个节点：
		Node* cur = parent->_right;
		Node* curL = cur->_left;
		Node* pparent = parent->_parent;
		//开始改变指向操作
		parent->_right = curL;
		if(curL)//注意：需要检查curL是否为空
			curL->_parent = parent;
		cur->_left = parent;
		parent->_parent = cur;
		//开始检查pparent
		if (parent == _root)
		{
			_root = cur;
			cur->_parent = nullptr;
		}
		else
		{
			//检查pparent的左右子节点
			if (pparent->_left == parent)
			{
				pparent->_left = cur;
				cur->_parent = pparent;
			}
			else
			{
				pparent->_right = cur;
				cur->_parent = pparent;
			}
		}
		//改变_bf值
		parent->_bf = 0;
		cur->_bf = 0;
	}
	void RotateR(Node* parent)
	{
		//同理:记录四个子节点
		Node* cur = parent->_left;
		Node* curR = cur->_right;
		Node* pparent = parent->_parent;
		//操作
		parent->_left = curR;
		if (curR)
			curR->_parent = parent;
		parent->_parent = cur;
		cur->_right = parent;
		if (parent == _root)
		{
			_root = cur;
			cur->_parent = nullptr;
		}
		else
		{
			//检查pparent的左右子节点
			if (pparent->_left == parent)
			{
				pparent->_left = cur;
				cur->_parent = pparent;
			}
			else
			{
				pparent->_right = cur;
				cur->_parent = pparent;
			}
		}
		//改变_bf值
		parent->_bf = 0;
		cur->_bf = 0;
	}
	void RotateLR(Node* parent)
	{
		//提前保留位置
		Node* cur = parent->_left;
		Node* curR = cur->_right;
		int bf = curR->_bf;
		//利用已实现的左右旋转来实现
		RotateL(parent->_left);
		RotateR(parent);
		//修改bf
		if (bf == 0)
		{
			parent->_bf = 0;
			cur->_bf = 0;
			curR->_bf = 0;
		}
		else if (bf == 1)
		{
			cur->_bf = -1;
			parent->_bf = 0;
			curR->_bf = 0;
		}
		else if (bf == -1)
		{
			parent->_bf = 1;
			cur->_bf = 0;
			curR->_bf = 0;
		}
		else
		{
			exit(-1);
		}
	}
	void RotateRL(Node* parent)
	{
		//提前保留位置
		Node* cur = parent->_right;
		Node* curL = cur->_left;
		int bf = curL->_bf;
		//利用已实现的右左旋转来实现
		RotateR(parent->_right);
		RotateL(parent);
		//修改bf
		if (bf == -1)
		{
			parent->_bf = 0;
			cur->_bf = 1;
			curL->_bf = 0;
		}
		else if (bf == 1)
		{
			parent->_bf = -1;
			cur->_bf = 0;
			curL->_bf = 0;
		}
		else if (bf == 0)
		{
			parent->_bf = 0;
			cur->_bf = 0;
			curL->_bf = 0;
		}
		else
		{
			exit(-1);
		}
	}
	
private:
	Node* _root = nullptr;
};

下面是红黑树的实现：

#pragma once

enum Color
{
	RED,
	BLACK
};
template <class T>
struct RBTreeNode
{
	//成员函数：
	//构造函数：
	RBTreeNode(const T& date)
		:_left(nullptr),_right(nullptr),_parent(nullptr),_date(date),_color(RED)
	{}
	//注意点：_color默认为红！！！
	//成员变量：
	RBTreeNode<T>* _left;
	RBTreeNode<T>* _right;
	RBTreeNode<T>* _parent;
	T _date;
	Color _color;
};

template<class T,class Ptr,class Ref>
struct RBTreeIterator
{
	typedef RBTreeNode<T> Node;
	typedef RBTreeIterator<T, Ptr, Ref> Self;
	RBTreeIterator(Node* node)
		:_node(node)
	{}
	//解引用
	Ref operator*()
	{
		return _node->_date;
	}
	//取地址：
	Ptr operator->()
	{
		return &(_node->_date);
	}
	//加减：
	//前置++
	Self& operator++()
	{
		//规则：1.如果有右节点，找右节点的最左节点
		//2.如果无右节点，找子是父的左树
		if (_node->_right)
		{
			//1.有右节点，找右节点的最左节点
			Node* subright = _node->_right;
			while (subright->_left)
			{
				subright = subright->_left;
			}
			_node = subright;
		}
		else
		{
			//2.无右节点，找子是父的左树
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur== parent->_right)//防一波root
			{
				cur = parent;
				parent = parent->_parent;
			}
			_node = parent;
		}
		return *this;
	}
	//后置++：
	Self& operator++(int)
	{
		Self s = *this;
		//规则：1.如果有右节点，找右节点的最左节点
		//2.如果无右节点，找子是父的左树
		if (_node->_right)
		{
			//1.有右节点，找右节点的最左节点
			Node* subright = _node->_right;
			while (subright->_left)
			{
				subright = subright->_left;
			}
			_node = subright;
		}
		else
		{
			//2.无右节点，找子是父的左树
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && cur == parent->_right)//防一波root
			{
				cur = parent;
				parent = parent->_parent;
			}
			_node = parent;
		}
		return s;
	}
	//--操作：
	//前置--：
	Self& operator--()
	{
		//规则：1.如果有左子树节点，找其最右节点
		//2.如果无左子树节点，找子树是父的右节点位置
		if (_node->_left)
		{
			Node* subL = _node->_left;
			while (subL->_right)
			{
				subL->_right;
			}
			_node = subL;
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && parent == cur->_left)
			{
				cur = parent;
				parent = parent->_parent;
			}
			_node = parent;
		}
		return *this;
	}
	//后置--
	Self& operator--(int)
	{
		Self s = *this;
		//规则：1.如果有左子树节点，找其最右节点
		//2.如果无左子树节点，找子树是父的右节点位置
		if (_node->_left)
		{
			Node* subL = _node->_left;
			while (subL->_right)
			{
				subL->_right;
			}
			_node = subL;
		}
		else
		{
			Node* cur = _node;
			Node* parent = cur->_parent;
			while (parent && parent == cur->_left)
			{
				cur = parent;
				parent = parent->_parent;
			}
			_node = parent;
		}
		return s;
	}
	bool operator!=(const Self& s)
	{
		return !(_node == s._node);
	}
	bool operator==(const Self& s)
	{
		return _node==s._node;
	}
	//成员变量:
	Node* _node;
};

template <class K,class T, class KeyOfT>
class RBTree
{
public:
	typedef RBTreeNode<T> Node;
	typedef RBTreeIterator<T, T*, T&> iterator;
	typedef RBTreeIterator<T, const T*, const T&> const_iterator;
	//迭代器：
	iterator begin()
	{
		Node* subL = _root;
		//找最左节点
		while (subL && subL->_left)
		{
			subL = subL->_left;
		}
		return iterator(subL);
	}
	iterator end()
	{
		return iterator(nullptr);
	}
	const_iterator begin()const
	{
		Node* subL = _root;
		while (subL && subL->_left)
		{
			subL = subL->_left;
		}
		return const_iterator(subL);
	}
	const_iterator end()const
	{
		return const_iterator(nullptr);
	}
	pair<iterator, bool> Insert(const T& date)
	{
		//插入分为两步操作：
		//第一步：插入该节点位置
		//1.检查_root是否为空
		if (_root == nullptr)
		{
			_root = new Node(date);
			//注意：规则：root节点颜色为黑
			_root->_color = BLACK;
			return make_pair(iterator(_root), true);
		}
		//2.利用两个Node*，找到要插入位置和其父节点位置
		Node* cur = _root;
		Node* parent = nullptr;
		KeyOfT kot; 
		while (cur)
		{
			if (kot(cur->_date)<kot(date))
			{
				parent = cur;
				cur = cur->_right;
			}
			else if (kot(cur->_date)> kot(date))
			{
				parent = cur;
				cur = cur->_left;
			}
			else
			{
				//注意：相等报错
				return make_pair(iterator(cur), false);;
			}
		}
		//3.开空间链接_parent
		cur = new Node(date);
		Node* newnode = cur;
		cur->_parent = parent;
		if (kot(parent->_date)< kot(cur->_date))
		{
			parent->_right = cur;
		}
		else
		{
			parent->_left = cur;
		}
		//第二步：变色+旋转
		while (parent && parent->_color == RED)
		{
			//1.找uncle
			Node* grandparent = parent->_parent;
			if (parent == grandparent->_left)
			{
				//分情况讨论：
				Node* uncle = grandparent->_right;
				if (uncle && uncle->_color == RED)
				{
					//1.uncle存在且为红
					grandparent->_color = RED;
					uncle->_color = BLACK;
					parent->_color = BLACK;
					//注意：这里不需要讨论是否为root情况，原因我们在循环判断中写了parent是否为空情况
					cur = grandparent;
					parent = cur->_parent;
				}
				else
				{
					//2.uncle不存在或者存在且为黑
					if (cur == parent->_left)
					{
						//直接右旋
						RotateR(grandparent);
						//变色
						parent->_color = BLACK;
						grandparent->_color = RED;
					}
					else
					{
						RotateL(parent);
						RotateR(grandparent);
						grandparent->_color = RED;
						cur->_color = BLACK;
					}
					//无论是哪种情况都会结束
					break;
				}
			}
			else//parent为grandparent右节点
			{
				//分情况讨论
				Node* uncle = grandparent->_left;
				//1.uncle存在且为红
				if (uncle && uncle->_color == RED)
				{
					//变色
					grandparent->_color = RED;
					uncle->_color = BLACK;
					parent->_color = BLACK;
					//注意：这里不需要讨论是否为root情况，原因我们在循环判断中写了parent是否为空情况
					cur = grandparent;
					parent = cur->_parent;
				}
				else
				{
					//2.uncle可能不存在可能存在且为黑
					if (cur == parent->_right)
					{
						//直接左旋
						RotateL(grandparent);
						//变色
						grandparent->_color = RED;
						parent->_color = BLACK;
					}
					else//cur位于左节点
					{
						//右左双旋
						RotateR(parent);
						RotateL(grandparent);
						cur->_color = BLACK;
						grandparent->_color = RED;
					}
					//无论是哪种情况都会结束
					break;
				}
			}
		}
		_root->_color = BLACK;
		return make_pair(iterator(newnode), true);
	}
	//三序遍历;
	void Preorder()
	{
		_Preorder(_root);
	}
	void Inorder()
	{
		_Inorder(_root);
	}
	void Postorder()
	{
		_Postorder(_root);
	}
	size_t size()
	{
		return _size(_root);
	}
	size_t height()
	{
		return _height(_root);
	}
	iterator find(const K& date)
	{
		Node* cur = _root;
		KeyOfT kot;
		while (cur)
		{
			if (kot(cur->_date)<date)
			{
				cur = cur->_right;
			}
			else if (kot(cur->_date)>date)
			{
				cur = cur->_left;
			}
			else
			{
				return iterator(cur);
			}
		}
		return end();
	}
	bool balance()
	{
		Node* cur = _root;
		if (cur && cur->_color == RED)
		{
			cout << "root节点为红" << endl;
			return false;
		}
		int stantard = 0;
		while (cur)
		{
			if (cur->_color == BLACK)
			{
				stantard++;
			}
			cur = cur->_left;
		}
		return _balance(_root, 0, stantard);
	}
	//查看旋转次数
	size_t GetRotate()
	{
		return rotatesize;
	}
private:
	bool _balance(Node* cur, int blacknum, int stantard)
	{
		if (cur == nullptr)
		{
			if (blacknum != stantard)
			{
				cout << "黑节点个数不匹配" << endl;
				return false;
			}
			return true;
		}
		//规则二：不能连续出现红节点
		if (cur->_color == RED && cur->_parent->_color == RED)
		{
			cout << "连续出现红节点" << endl;
			return false;
		}
		if (cur->_color == BLACK)
		{
			blacknum++;
		}
		return _balance(cur->_left, blacknum, stantard) && _balance(cur->_right, blacknum, stantard);
	}
	size_t _height(Node* root)
	{
		if (root == nullptr)
			return 0;
		else
			return max(_height(root->_left), _height(root->_right)) + 1;
	}
	size_t _size(Node* root)
	{
		if (root == nullptr)
			return 0;
		else
			return _size(root->_left) + _size(root->_right) + 1;
	}
	void _Postorder(Node* root)
	{
		if (root == nullptr)
			return;
		_Postorder(root->_left);
		_Postorder(root->_right);
		cout << root->_date<< endl;
	}
	void _Inorder(Node* root)
	{
		if (root == nullptr)
			return;
		_Inorder(root->_left);
		cout << root->_date << endl;
		_Inorder(root->_right);
	}
	void _Preorder(Node* root)
	{
		if (root == nullptr)
			return;
		cout << root->_date << endl;
		_Preorder(root->_left);
		_Preorder(root->_right);
	}
	//旋转操作：
	//左旋：
	void RotateL(Node* parent)
	{
		rotatesize++;
		Node* subR = parent->_right;
		Node* subRL = subR->_left;
		Node* pparent = parent->_parent;
		//链接
		if(subRL)//防止subRL为空情况
			subRL->_parent = parent;
		parent->_right = subRL;
		subR->_left = parent;
		parent->_parent = subR;
		if (parent == _root)
		{
			_root = subR;
			subR->_parent = nullptr;
		}
		else
		{
			if (pparent->_left == parent)
			{
				pparent->_left = subR;
			}
			else
			{
				pparent->_right = subR;
			}
			subR->_parent = pparent;
		}
	}
	//右旋:
	void RotateR(Node* parent)
	{
		rotatesize++;
		Node* subL = parent->_left;
		Node* subLR = subL->_right;
		Node* pparent = parent->_parent;
		if (subLR)
			subLR->_parent = parent;
		parent->_left = subLR;
		subL->_right = parent;
		parent->_parent = subL;
		if (parent == _root)
		{
			_root = subL;
			subL->_parent = nullptr;
		}
		else
		{
			if (pparent->_left == parent)
			{
				pparent->_left = subL;
			}
			else
			{
				pparent->_right = subL;

			}
			subL->_parent = pparent;
		}
	}
private:
	Node* _root = nullptr;
	size_t rotatesize = 0;
};

我们这里就和系统一样直接套用红黑树实现吗，map和set

如下：

#pragma once

#include "RBTree.h"

namespace cx
{
	template<class K>
	class set
	{
		struct KeyOfT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};
	public:
		typedef typename RBTree<K, const K, KeyOfT>::iterator iterator;
		typedef typename RBTree<K, const K, KeyOfT>::const_iterator const_iterator;
		iterator begin()
		{
			return _t.begin();
		}
		iterator end()
		{
			return _t.end();
		}
		const_iterator begin()const
		{
			return _t.begin();
		}
		const_iterator end()const
		{
			return _t.end();
		}
		iterator Find(const K& date)
		{
			return _t.find(date);
		}
		pair<iterator, bool> Insert(const K& date)
		{
			return _t.Insert(date);
		}
	private:
		RBTree<K, const K, KeyOfT> _t;
	};
};

#pragma once

#include "RBTree.h"

namespace cx
{
	template<class K,class V>
	class map
	{
		struct KeyOfT
		{
			const K& operator()(const pair<K, V>& kv)
			{
				return kv.first;
			}
		};
	public:
		typedef typename RBTree<K, pair<const K, V>, KeyOfT>::iterator iterator;
		typedef typename RBTree<K, pair<const K, V>, KeyOfT>::const_iterator const_iterator;
		iterator begin()
		{
			return _p.begin();
		}
		iterator end()
		{
			return _p.end();
		}
		const_iterator begin()const
		{
			return _p.begin();
		}
		const_iterator end()const
		{
			return _p.end();
		}
		pair<iterator, bool> Insert(const pair<K, V>& kv)
		{
			return _p.Insert(kv);
		}
		iterator Find(const K& date)
		{
			return _p.find(date);
		}
		V& operator[](const K& key)
		{
			pair<iterator, bool> ret = Insert(make_pair(key, V()));
			return (ret.first)->second;
			//ret.first是iterator,iterator的second为（ RBTreeIterator<T, T*, T&> iterator）T*
			//T* 在这里为 <class K,class T, class KeyOfT> 为第二个参数pair<const K, V>
			//所以这里结果为pair
		}
	private:
		RBTree<K, pair<const K, V>, KeyOfT> _p;
	};
};

这里我也写过测试用例：

#include <iostream>

using namespace std;
#include "map.h"
#include "set.h"
#include "RBTree.h"
using namespace cx;


//
//void test_map2()
//{
//	string arr[] = { "ƻ", "", "ƻ", "", "ƻ", "ƻ", "",
//"ƻ", "㽶", "ƻ", "", "㽶", "ݮ" };
//	map<string, int> countMap;
//	for (auto& e : arr)
//	{
//		/*if (e == "ݮ")
//		{
//			int i = 0;
//		}*/
//		countMap[e]++;
//	}
//
//	for (auto& kv : countMap)
//	{
//		cout << kv.first << ":" << kv.second << endl;
//	}
//	cout << endl;
//}

//void test_set1()
//{
//	set<int> s;
//	int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
//	for (auto e : a)
//	{
//		s.insert(e);
//	}
//
//	set<int>::iterator it = s.begin();
//	while (it != s.end())
//	{
//		//if(*it % 2 == 0)
//		//	*it += 100;
//
//		cout << *it << " ";
//		++it;
//	}
//	cout << endl;
//}
//}


//void test_map1()
//{
//	map<string, string> dict;
//	dict.insert(pair<string, string>("sort", "排序"));
//
//	//pair<string, string> kv("string", "字符串");
//	pair<string, string> kv = { "string", "字符串" };
//	dict.insert(kv);
//
//	// C++11 多参数隐式类型转换(构造函数)
//	dict.insert({ "apple", "苹果" });
//
//	// C++98
//	dict.insert(make_pair("sort", "排序"));
//
//	//map<string, string>::iterator it = dict.begin();
//	auto it = dict.begin();
//	while (it != dict.end())
//	{
//		//cout << *it << endl;
//		//cout << (*it).first << (*it).second << endl;
//		cout << it->first << it->second << endl;
//		++it;
//	}
//	cout << endl;
//
//	for (auto& kv : dict)
//	{
//		cout << kv.first << ":" << kv.second << endl;
//	}
//	cout << endl;
//}
//
//void test_map2()
//{
//	// key相同，value不同，不会插入也不会更新
//	map<string, string> dict;
//	dict.insert(make_pair("sort", "排序"));
//	dict.insert(make_pair("string", "字符串"));
//	dict.insert(make_pair("sort", "xxx"));
//
//	dict["left"]; // 插入
//	cout << dict["sort"] << endl; // 查找
//	dict["sort"] = "xxx"; // 修改
//	dict["right"] = "右边"; // 插入+修改
//
//	for (auto& kv : dict)
//	{
//		cout << kv.first << ":" << kv.second << endl;
//	}
//	cout << endl;
//}
//
//void test_map3()
//{
//	multimap<string, string> dict;
//	dict.insert(make_pair("sort", "排序"));
//	dict.insert(make_pair("string", "字符串"));
//	dict.insert(make_pair("sort", "xxx"));
//	dict.insert(make_pair("sort", "排序"));
//
//	for (auto& kv : dict)
//	{
//		cout << kv.first << ":" << kv.second << endl;
//	}
//	cout << endl;
//}

//
//void test_map4()
//{
//	string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜",
//"苹果", "香蕉", "苹果", "西瓜", "香蕉", "草莓" };
//	map<string, int> countMap;
//	//for (auto& e : arr)
	//{
	//	map<string, int>::iterator it = countMap.find(e);
	//	if (it != countMap.end())
	//	{
	//		it->second++;
	//	}
	//	else
	//	{
	//		countMap.insert(make_pair(e, 1));
	//	}
	//}

	//for (auto& e : arr)
	//{
	//	pair<map<string, int>::iterator, bool> ret;
	//	ret = countMap.insert(make_pair(e, 1));

	//	// 已经存在了
	//	if (ret.second == false)
	//	{
	//		ret.first->second++;
	//	}
	//}

//	for (auto& e : arr)
//	{
//		countMap[e]++;
//	}
//
//	for (auto& kv : countMap)
//	{
//		//kv.first = "xxx";
//		//kv.second = 1;
//		cout << kv.first << ":" << kv.second << endl;
//	}
//	cout << endl;
//}

void test_set1()
{
	cx::set<int> s;
	int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	for (auto e : a)
	{
		s.Insert(e);
	}
	set<int>::iterator it = s.begin();
	while (it != s.end())
	{
		//if(*it % 2 == 0)
		//	*it += 100;
		cout << *it << " ";
		++it;
	}
	cout << endl;
}
void test_map1()
{
	map<int, int> m;
	int a[] = { 4, 2, 6, 1, 3, 5, 15, 7, 16, 14 };
	for (auto e : a)
	{
		m.Insert(make_pair(e, e));
	}
	map<int, int>::iterator it = m.begin();
	while (it != m.end())
	{
		//it->first += 100;
		it->second += 100;

		cout << it->first << ":" << it->second << endl;
		++it;
	}
	cout << endl;
}

void test_map2()
{
	string arr[] = { "ƻ", "", "ƻ", "", "ƻ", "ƻ", "","ƻ", "㽶", "ƻ", "", "㽶", "ݮ" };
	map<string, int> countMap;
	for (auto& e : arr)
	{
		countMap[e]++;
	}
	for (auto& kv : countMap)
	{
		cout << kv.first << ":" << kv.second << endl;
	}
	cout << endl;
}
void test_set2()
{
	set<int> s;
	s.Insert(3);
	s.Insert(1);
	s.Insert(5);
	s.Insert(7);
	for (auto e : s)
	{
		cout << e << " ";
	}
	cout << endl;
}
void test_map3()
{
	string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜",
"苹果", "香蕉", "苹果", "西瓜", "香蕉", "草莓" };
	map<string, int> countMap;
	for (auto& e : arr)
	{
		countMap[e]++;
	}
	for (auto& kv : countMap)
	{
		cout << kv.first << ":" << kv.second << endl;
	}
	cout << endl;
}
int main()
{
	//test_map1();
	//test_set1();
	//test_map2();
	//test_set2();
	test_map3();
	return 0;
}

二.multimap/multiset

这两个也是用红黑树实现的，所以大家只需要去能清楚和map/set的区别即可！！！

区别如下：

1.multiset中在底层中存储的是的键值对

2. mtltiset的插入接口中只需要插入即可

3. 与set的区别是，multiset中的元素可以重复，set是中value是唯一的

4. 使用迭代器对multiset中的元素进行遍历，可以得到有序的序列

5. multiset中的元素不能修改

6. 在multiset中找某个元素，时间复杂度为$O(log_2 N)$

7. multiset的作用：可以对元素进行排序

8.multimap和map的唯一不同就是：map中的key是唯一的，而multimap中key是可以 重复的。

还需要注意的一点是：

只有map支持[]！！！

三.unordered_set/map

与之前不同这里使用哈希实现的

如果不想出现哈希冲突，我们可以直接定值法,但是容易出现空间消耗过大情况

所以我们更倾向于解决哈希冲突，方法如下：

1.闭散列：

我们可以直接用线性探测解决，也可以用二次探测解决：

实现如下：

#pragma once


namespace cx_open_address
{
	//一.哈希冲突线性探测解决问题法：
	/
	//以下插入、查找、删除操作都只适用int类型：
	需要表示状态：
	//enum State
	//{
	//	EMPTY,
	//	EXIST,
	//	DELETE
	//};
	哈希数据：
	//template <class K,class V>
	//class HashDate
	//{
	//public:
	//	pair<K, V> _kv;
	//	State _state = EMPTY;//默认为空
	//};

	哈希table实现：
	//template<class K,class V>
	//class Hashtable
	//{
	//public:
	//	Hashtable(size_t size = 10)
	//	{
	//		_tables.resize(size);//用resize可以直接先开到size=capacity大小
	//	}
	//	
	//	
	//	//以下插入、查找、删除操作都只适用int类型：
	//	//插入操作：
	//	bool Insert(const pair<K, V>& kv)
	//	{
	//		//检查是否存在
	//		if (Find(kv.first))
	//			return false;
	//		//利用平衡因子解决扩容问题：
	//		//if(_n*1.0/_tables.size()>=0.7)
	//		if (_n * 10 / _tables.size() >= 7)
	//		{
	//			//利用新hashtables来实现扩容
	//			Hashtable<K, V> newtables(_tables.size() * 2);
	//			//遍历原tables，插入到新tables
	//			for (auto& e : _tables)
	//			{
	//				if (e._state == EXIST)
	//				{
	//					newtables.Insert(e._kv);
	//				}
	//			}
	//			//将新tables与原tables交换
	//			_tables.swap(newtables._tables);
	//		}
	//		//正常的线性探测插入操作：
	//		size_t hashi = kv.first % _tables.size();
	//		while (_tables[hashi]._state == EXIST)
	//		{
	//			hashi++;
	//			hashi %= _tables.size();
	//		}
	//		//插入操作：
	//		_tables[hashi]._kv = kv;
	//		_tables[hashi]._state = EXIST;
	//		_n++;//统计的元素个数也增加
	//		return true;
	//	}
	//	HashDate<K, V>* Find(const K& key)
	//	{
	//		//这里是线性探测
	//		//规则：如果当前位置已经有值了，向后查找空位置
	//		size_t hashi = key % _tables.size();//假设现在数据为int
	//		//后面我们在回到string等其他类型
	//		while (_tables[hashi]._state != EMPTY)
	//		{
	//			//当前位置已经存在数据，开始查找
	//			//情况一：如果我们当前位置存的数据就是key
	//			if (key == _tables[hashi]._kv.first &&
	//				_tables[hashi]._state == EXIST)
	//			{
	//				return &_tables[hashi];
	//			}
	//			//情况二：起始位置存的是其他值，现在我们要向后找
	//			hashi++;
	//			//注意：%
	//			hashi %= _tables.size();
	//		}
	//		//如果没位置，返回nullptr
	//		return nullptr;
	//	}
	//	bool Erase(const K& key)
	//	{
	//		//利用Find查找
	//		HashDate<K, V>* ans = Find(key);
	//		//如果存在就删除
	//		if (ans)
	//		{
	//			_n--;
	//			ans->_state = DELETE;
	//			return true;
	//		}
	//		else
	//		{
	//			//不存在，返回false
	//			return false;
	//		}
	//	}
	//private:
	//	vector<HashDate<K, V>> _tables;
	//	size_t _n = 0;//统计个数
	//};
	//下面我们写出适用所有类型的写法：
	//需要表示状态：
	enum State
	{
		EMPTY,
		EXIST,
		DELETE
	};
	//哈希数据：
	template <class K, class V>
	class HashDate
	{
	public:
		pair<K, V> _kv;
		State _state = EMPTY;//默认为空
	};
	template<class K>
	struct HashFunc
	{
		size_t operator()(const K& key)
		{
			//返回size
			return (size_t)key;
		}
	};
	//模版特化：
	//string类：
	template<>
	struct HashFunc<string>
	{
		size_t operator()(const string& s)
		{
			size_t hash = 0;
			//
			for (auto e : s)
			{
				hash += e;
				hash *= 131;
			}
			return hash;
		}
	};
	//日期类特化：
	struct Date
	{
		int _year;
		int _month;
		int _day;
	};
	template<>
	struct HashFunc<Date>
	{
		size_t operator()(const Date& d)
		{
			size_t hash = 0;
			hash += d._year;
			hash *= 131;
			hash += d._month;
			hash *= 131;
			hash += d._day;
			hash *= 131;
			return hash;
		}
	};
	//pesron类特化：
	struct Person
	{
		string _name;
		string _id;   // 身份证号码
		string _tel;
		int _age;
		string _class;
		string _address;
	};
	template<>
	struct HashFunc<Person>
	{
		size_t operator()(const Person& p)
		{
			size_t hash = 0;
			//选择一项进行计算：
			for (auto e : p._id)
			{
				hash += e;
				hash *= 131;
			}
			return hash;
		}
	};
	//哈希table实现：
	template<class K, class V,class Hash=HashFunc<K>>
	class Hashtable
	{
	public:
		Hashtable(size_t size = 10)
		{
			_tables.resize(size);//用resize可以直接先开到size=capacity大小
		}
		//多类型实现：
		//插入操作：
		bool Insert(const pair<K, V>& kv)
		{
			//检查是否存在
			if (Find(kv.first))
				return false;
			//利用平衡因子解决扩容问题：
			//if(_n*1.0/_tables.size()>=0.7)
			if (_n * 10 / _tables.size() >= 7)
			{
				//利用新hashtables来实现扩容
				Hashtable<K, V> newtables(_tables.size() * 2);
				//遍历原tables，插入到新tables
				for (auto& e : _tables)
				{
					if (e._state == EXIST)
					{
						newtables.Insert(e._kv);
					}
				}
				//将新tables与原tables交换
				_tables.swap(newtables._tables);
			}
			//正常的线性探测插入操作：
			Hash hs;
			size_t hashi = hs(kv.first) % _tables.size();
			while (_tables[hashi]._state == EXIST)
			{
				hashi++;
				hashi %= _tables.size();
			}
			//插入操作：
			_tables[hashi]._kv = kv;
			_tables[hashi]._state = EXIST;
			_n++;//统计的元素个数也增加
			return true;
		}
		HashDate<K, V>* Find(const K& key)
		{
			//这里是线性探测
			//规则：如果当前位置已经有值了，向后查找空位置
			Hash hs;
			size_t hashi = hs(key) % _tables.size();//假设现在数据为int
			//后面我们在回到string等其他类型
			while (_tables[hashi]._state != EMPTY)
			{
				//当前位置已经存在数据，开始查找
				//情况一：如果我们当前位置存的数据就是key
				if (key == _tables[hashi]._kv.first &&
					_tables[hashi]._state == EXIST)
				{
					return &_tables[hashi];
				}
				//情况二：起始位置存的是其他值，现在我们要向后找
				hashi++;
				//注意：%
				hashi %= _tables.size();
			}
			//如果没位置，返回nullptr
			return nullptr;
		}
		bool Erase(const K& key)
		{
			//利用Find查找
			HashDate<K, V>* ans = Find(key);
			//如果存在就删除
			if (ans)
			{
				_n--;
				ans->_state = DELETE;
				return true;
			}
			else
			{
				//不存在，返回false
				return false;
			}
		}
	private:
		vector<HashDate<K, V>> _tables;
		size_t _n = 0;//统计个数
	};
	
	///
	//哈希冲突二次探测解决问题法：
	//与线性探测不同点：不再是一个个向后查找，而是一个数的次方不断增大方式查找空余空间，其余大体相同
	//这里不进行实现！！！
}

2.开散列：

//不管是线性探测还是二次探测，都是闭散列解决哈希冲突，下面我们实现开散列解决哈希冲突
namespace cx_hash_bucket//cx_close_address
{
	//每个节点存放的值：
	template<class K,class V>
	struct HashNode
	{
		HashNode(const pair<K, V>& kv)
			:_next(nullptr)
			, _kv(kv)
		{}
		HashNode<K, V>* _next;
		pair<K, V> _kv;
	};
	template<class K>
	struct HashFunc
	{
		size_t operator()(const K& key)
		{
			//返回size
			return (size_t)key;
		}
	};
	//模版特化：
	//string类：
	template<>
	struct HashFunc<string>
	{
		size_t operator()(const string& s)
		{
			size_t hash = 0;
			//
			for (auto e : s)
			{
				hash += e;
				hash *= 131;
			}
			return hash;
		}
	};
	//日期类特化：
	struct Date
	{
		int _year;
		int _month;
		int _day;
	};
	template<>
	struct HashFunc<Date>
	{
		size_t operator()(const Date& d)
		{
			size_t hash = 0;
			hash += d._year;
			hash *= 131;
			hash += d._month;
			hash *= 131;
			hash += d._day;
			hash *= 131;
			return hash;
		}
	};
	//pesron类特化：
	struct Person
	{
		string _name;
		string _id;   // 身份证号码
		string _tel;
		int _age;
		string _class;
		string _address;
	};
	template<>
	struct HashFunc<Person>
	{
		size_t operator()(const Person& p)
		{
			size_t hash = 0;
			//选择一项进行计算：
			for (auto e : p._id)
			{
				hash += e;
				hash *= 131;
			}
			return hash;
		}
	};
	template<class K,class V,class Hash= HashFunc<K>>
	class Hashtable
	{
		typedef HashNode<K, V> Node;
	public:
		Hashtable(const size_t size=10)
		{
			_tables.resize(size,nullptr);
			_n = 0;
		}
		~Hashtable()
		{
			//深拷贝
			for (size_t i = 0; i < _tables.size(); i++)
			{
				Node* cur = _tables[i];
				while (cur)
				{
					Node* next = cur->_next;
					delete cur;
					cur = next;
				}
				_tables[i] = nullptr;
			}
		}
		//操作;
		bool Insert(const pair<K, V>& kv)
		{
			//同理
			if (Find(kv.first))
				return false;
			//当负载因子达到一扩容
			Hash hs;
			if (_n == _tables.size())
			{
				vector<Node*> newtables(_tables.size() * 2,nullptr);
				//遍历原数组
				for (int i = 0; i < _tables.size(); i++)
				{
					Node* cur=_tables[i];
					while (cur)
					{
						Node* next=cur->_next;
						//头插到新表
						size_t hashi = hs(cur->_kv.first) % newtables.size();
						cur->_next = newtables[hashi];
						newtables[hashi] = cur;
						cur = next;
					}
					_tables[i] = nullptr;
				}
				//交换
				_tables.swap(newtables);
			}
			//头插插入
			size_t hashi = hs(kv.first) % _tables.size();
			Node* newnode = new Node(kv);
			newnode->_next = _tables[hashi];
			_tables[hashi] = newnode;
			_n++;
			return true;
		}
		Node* Find(const K& key)
		{
			Hash hs;
			size_t hashi = hs(key) % _tables.size();
			Node* cur = _tables[hashi];
			while (cur)
			{
				if (cur->_kv.first == key)
				{
					return cur;
				}
				cur = cur->_next;
			}
			return nullptr;
		}
		bool Erase(const K& key)
		{
			Hash hs;
			size_t hashi = hs(key) % _tables.size();
			Node* cur = _tables[hashi];
			Node* prev = nullptr;
			while (cur)
			{
				if (cur->_kv.first == key)
				{
					//删除注意分情况:
					//1.prev为空
					//2.删除非头
					if (prev)
					{
						prev->_next = cur->_next;
					}
					else
					{
						_tables[hashi] = cur->_next;
					}
					delete cur;
					cur = nullptr;
					_n--;
					return true;
				}
				prev = cur;
				cur = cur->_next;
			}
			return false;
		}
	private:
		vector<Node*> _tables;
		size_t _n = 0;
	};
}

下面我们利用开散列实现STL中的哈希：

#pragma once
#include "hash.h"

namespace cx
{
	template<class K,class V,class Hash = HashFunc<K>>
	class myunordered_map
	{
		struct MapKeyOfT
		{
			const K& operator()(const pair<K,V>& kv)
			{
				return kv.first;
			}
		};
	public:
		typedef typename Hashtable<K, const K, MapKeyOfT, Hash>::iterator iterator;
		iterator begin()
		{
			return _ht.begin();
		}
		iterator end()
		{
			return _ht.end();
		}
		bool Insert(const pair<K,V>& kv)
		{
			return _ht.Insert(kv);
		}
		bool Erase(const K& key)
		{
			return _ht.Erase(key);
		}
	private:
		Hashtable<K, pair<const K,V>, MapKeyOfT, Hash> _ht;
	};
}

#pragma once
#include "hash.h"

namespace cx
{
	template<class K,class Hash= HashFunc<K>>
	class myunordered_set
	{
		struct SetKeyOfT
		{
			const K& operator()(const K& key)
			{
				return key;
			}
		};
	public:
		typedef typename Hashtable<K, const K, SetKeyOfT, Hash>::iterator iterator;
		iterator begin()
		{
			return _ht.begin();
		}
		iterator end()
		{
			return _ht.end();
		}
		bool Insert(const K& key)
		{
			return _ht.Insert(key);
		}
		bool Erase(const K& key)
		{
			return _ht.Erase(key);
		}
	private:
		Hashtable<K, const K, SetKeyOfT, Hash> _ht;
	};
}
#pragma once

//cx_close_address
//每个节点存放的值：
template<class T>
struct HashNode
{
	HashNode(const T& data)
		:_next(nullptr)
		, _data(data)
	{}
	HashNode<T>* _next;
	T _data;
};
template<class K>
struct HashFunc
{
	size_t operator()(const K& key)
	{
		//返回size
		return (size_t)key;
	}
};
//模版特化：
//string类：
template<>
struct HashFunc<string>
{
	size_t operator()(const string& s)
	{
		size_t hash = 0;
		//
		for (auto e : s)
		{
			hash += e;
			hash *= 131;
		}
		return hash;
	}
};
//日期类特化：
struct Date
{
	int _year;
	int _month;
	int _day;
};
template<>
struct HashFunc<Date>
{
	size_t operator()(const Date& d)
	{
		size_t hash = 0;
		hash += d._year;
		hash *= 131;
		hash += d._month;
		hash *= 131;
		hash += d._day;
		hash *= 131;
		return hash;
	}
};
//pesron类特化：
struct Person
{
	string _name;
	string _id;   // 身份证号码
	string _tel;
	int _age;
	string _class;
	string _address;
};
template<>
struct HashFunc<Person>
{
	size_t operator()(const Person& p)
	{
		size_t hash = 0;
		//选择一项进行计算：
		for (auto e : p._id)
		{
			hash += e;
			hash *= 131;
		}
		return hash;
	}
};
// 前置声明
template<class K, class T, class KeyOfT, class Hash>
class Hashtable;
template<class K, class T, class KeyOfT, class Hash>
struct __HTIterator
{
	typedef HashNode<T> Node;
	typedef Hashtable<K, T, KeyOfT, Hash> HT;
	typedef __HTIterator<K, T, KeyOfT, Hash> Self;
	//常见操作：
	__HTIterator(Node* node,HT* ht)
		:_node(node),_ht(ht)
	{}
	T& operator*()
	{
		return _node->_data;
	}
	Self& operator++()
	{
		if (_node->_next)
		{
			_node = _node->_next;
		}
		else
		{
			//当前桶已满，找下一个桶
			KeyOfT kot;
			Hash hs;
			size_t hashi = hs(kot(_node->_data)) % _ht->_tables.size();
			hashi++;
			while (hashi < _ht->_tables.size())
			{
				if (_ht->_tables[hashi])
				{
					_node = _ht->_tables[hashi];
					break;
				}
				hashi++;
			}
			if (hashi == _ht->_tables.size())
			{
				_node = nullptr;
			}
		}
		return *this;
	}
	Self& operator++(int)
	{
		Self tmp = *this;
		if (_node->_next)
		{
			_node = _node->_next;
		}
		else
		{
			//当前桶已满，找下一个桶
			KeyOfT kot;
			Hash hs;
			size_t hashi = hs(kot(_node->_data)) % _ht->_tables.size();
			hashi++;
			while (hashi < _ht->_tables.size())
			{
				if (_ht->_tables[hashi])
				{
					_node = _ht._tables[hashi];
					break;
				}
				hashi++;
			}
			if (hashi == _ht->_tables.size())
			{
				_node = nullptr;
			}
		}
		return tmp;
	}
	Self& operator--()
	{
		KeyOfT kot;
		Hash hs;
		size_t hashi = hs(kot(_node->_data)) % _ht->_tables.size();
		if (_ht->_tables[hashi] == _node)
		{
			//向hashi减小的方向查找
			Node* cur = nullptr;
			for (size_t i = hashi - 1; i >= 0; i--)
			{
				if (_ht->_tables[i])
				{
					cur = _ht._tables[i];
				}
			}
			while (cur->_next != nullptr)
			{
				cur = cur->_next;
			}
			_node = cur;
		}
		else
		{
			Node* cur = _ht->_tables[hashi];
			Node* prev = nullptr;
			while (cur != _node)
			{
				prev = cur;
				cur = cur->_next;
			}
			_node = prev;
		}
		return *this;
	}
	Self& operator--(int)
	{
		Self tmp = *this;
		KeyOfT kot;
		Hash hs;
		size_t hashi = hs(kot(_node->_data)) % _ht->_tables.size();
		if (_ht->_tables[hashi] == _node)
		{
			//向hashi减小的方向查找
			Node* cur = nullptr;
			for (size_t i = hashi - 1; i >= 0; i--)
			{
				if (_ht->_tables[i])
				{
					cur = _ht._tables[i];
				}
			}
			while (cur->_next != nullptr)
			{
				cur = cur->_next;
			}
			_node = cur;
		}
		else
		{
			Node* cur = _ht->_tables[hashi];
			Node* prev = nullptr;
			while (cur != _node)
			{
				prev = cur;
				cur = cur->_next;
			}
			_node = prev;
		}
		return tmp;
	}
	bool operator!=(const Self& s)
	{
		return _node != s._node;
	}
	bool operator==(const Self& s)
	{
		return _node == s._node;
	}
	Node* _node;
	HT* _ht;
};
template<class K, class T, class KeyOfT,class Hash>
class Hashtable
{
	typedef HashNode<T> Node;
	template<class K, class T, class KeyOfT, class Hash>
	friend struct __HTIterator;
public:
	typedef __HTIterator<K, T, KeyOfT, Hash> iterator;
	iterator begin()
	{
		for (size_t i = 0; i < _tables.size(); i++)
		{
			if (_tables[i])
			{
				return iterator(_tables[i], this);
			}
		}
		return end();
	}
	iterator end()
	{
		return iterator(nullptr, this);
	}
	Hashtable(const size_t size = 10)
	{
		_tables.resize(size, nullptr);
		_n = 0;
	}
	~Hashtable()
	{
		//深拷贝
		for (size_t i = 0; i < _tables.size(); i++)
		{
			Node* cur = _tables[i];
			while (cur)
			{
				Node* next = cur->_next;
				delete cur;
				cur = next;
			}
			_tables[i] = nullptr;
		}
	}
	//操作;
	bool Insert(const T& data)
	{
		KeyOfT kot;
		if (Find(kot(data)))
			return false;
		//当负载因子达到一扩容
		Hash hs;
		if (_n == _tables.size())
		{
			vector<Node*> newtables(_tables.size() * 2, nullptr);
			//遍历原数组
			for (int i = 0; i < _tables.size(); i++)
			{
				Node* cur = _tables[i];
				while (cur)
				{
					Node* next = cur->_next;
					//头插到新表
					size_t hashi = hs(kot(cur->_data)) % newtables.size();
					cur->_next = newtables[hashi];
					newtables[hashi] = cur;
					cur = next;
				}
				_tables[i] = nullptr;
			}
			//交换
			_tables.swap(newtables);
		}
		//头插插入
		size_t hashi = hs(kot(data)) % _tables.size();
		Node* newnode = new Node(data);
		newnode->_next = _tables[hashi];
		_tables[hashi] = newnode;
		_n++;
		return true;
	}
	Node* Find(const K& key)
	{
		KeyOfT kot;
		Hash hs;
		size_t hashi = hs(key) % _tables.size();
		Node* cur = _tables[hashi];
		while (cur)
		{
			if (kot(cur->_data) == key)
			{
				return cur;
			}
			cur = cur->_next;
		}
		return nullptr;
	}
	bool Erase(const K& key)
	{
		KeyOfT kot;
		Hash hs;
		size_t hashi = hs(key) % _tables.size();
		Node* cur = _tables[hashi];
		Node* prev = nullptr;
		while (cur)
		{
			if (kot(cur->_data)== key)
			{
				//删除注意分情况:
				//1.prev为空
				//2.删除非头
				if (prev)
				{
					prev->_next = cur->_next;
				}
				else
				{
					_tables[hashi] = cur->_next;
				}
				delete cur;
				cur = nullptr;
				_n--;
				return true;
			}
			prev = cur;
			cur = cur->_next;
		}
		return false;
	}
private:
	vector<Node*> _tables;
	size_t _n = 0;
};

测试用例：

#include <iostream>
using namespace std;
#include <string>
#include <vector>

//#include "hash.h"
#include "unordered_map.h"
#include "unordered_set.h"

void test_set1()
{
	cx::myunordered_set<int> us;
	us.Insert(3);
	us.Insert(1);
	us.Insert(5);
	us.Insert(15);
	us.Insert(45);
	us.Insert(7);
	cx::myunordered_set<int>::iterator it = us.begin();
	while (it != us.end())
	{
		//*it += 100;
		cout << *it << " ";
		++it;
	}
	cout << endl;
	for (auto e : us)
	{
		cout << e << " ";
	}
	cout << endl;
}
void test_map1()
{
	cx::myunordered_map<string, string> dict;
	dict.Insert(make_pair("sort", ""));
	dict.Insert(make_pair("left", ""));
	dict.Insert(make_pair("right", "ұ"));
}
int main()
{
	//test_set1();
	test_map1();
	return 0;
}

最后，感谢大家的支持！！！

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1640453.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

MFC 列表控件删除实例（源码下载）

MFC 列表控件删除实例（源码下载）

1、本程序基于前期我的博客文章《MFC下拉菜单打钩图标存取实例&#xff08;源码下载) 》 2、程序功能选中列表控件某一项&#xff0c;删除按钮由禁止变为可用&#xff0c;点击删除按钮&#xff0c;选中的项将删除。 3、首先在主界面添加一个删除参数按钮。 4、在myDlg.cpp 文件…
阅读更多...
Python语言零基础入门——文件

Python语言零基础入门——文件

目录 一、文件的基本概念 1.文件 2.绝对路径与相对路径 3.打开文件的模式 二、文件的读取 三、文件的追加 四、文件的写入 五、with语句 六、csv文件 1.csv文件的读取 2.csv文件的写入 七、练习题&#xff1a;实现日记本 一、文件的基本概念 1.文件 文件是以计算…
阅读更多...
win10禁止自动更新的终极方法

win10禁止自动更新的终极方法

添加注册表值 1.运行&#xff0c;输入regedit 2.打开注册表编辑器依次进入以下路径“计算机\HKEY_LOCAL_MACHINE\SOFTWARE\Microsoft\WindowsUpdate\UX\Settings”。 3.在Settings项中&#xff0c;新建DWORD&#xff08;32位&#xff09;值(D)&#xff0c;重命名为以下命名“Fl…
阅读更多...
python判断大图中包含小图并输出位置总结

python判断大图中包含小图并输出位置总结

python判断大图中包含小图并输出位置总结 没啥可说的&#xff0c;项目遇到了就直接上代码&#xff0c;可以减轻劳动力&#xff0c;花最少得时间实现应用功能。 import cv2 # 读取大图片和小图片的路径 img_big cv2.imread(big_image.png) img_small cv2.imread(small_image…
阅读更多...
使用protoc-jar-maven-plugin生成grpc项目

使用protoc-jar-maven-plugin生成grpc项目

在《使用protobuf-maven-plugin生成grpc项目》中我们使用protobuf-maven-plugin完成了grpc代码的翻译。本文我们将只是替换pom.xml中的部分内容&#xff0c;使用protoc-jar-maven-plugin来完成相同的功能。总体来说protoc-jar-maven-plugin方案更加简便。 环境 见《使用proto…
阅读更多...
数据结构--顺序表经典OJ题

数据结构--顺序表经典OJ题

例1&#xff1a;合并有序顺序表 给你两个按 非递减顺序 排列的整数数组 nums1 和 nums2&#xff0c;另有两个整数 m 和 n &#xff0c;分别表示 nums1 和 nums2 中的元素数目。请你 合并 nums2 到 nums1 中&#xff0c;使合并后的数组同样按 非递减顺序 排列。 注意&#xff…
阅读更多...
R可视化：分组频率分布直方图和密度图

R可视化：分组频率分布直方图和密度图

介绍 ggplot2绘制分组频率分布直方图和密度图 加载R包 knitr::opts_chunk$set(message FALSE, warning FALSE) library(tidyverse) library(patchwork) library(ggpubr) library(rstatix)# rm(list ls()) options(stringsAsFactors F) options(future.globals.maxSize …
阅读更多...
数据结构与算法---树

数据结构与算法---树

数据结构可视化网址 Structure Visualization: https://www.cs.usfca.edu/~galles/visualization/Totuma: https://www.totuma.cn/Algorithm Visualizer: https://algorithm-visualizer.org/ 构建二叉树 // C#include<stdio.h> #include<stdlib.h>typedef char T…
阅读更多...
电脑找不到msvcp140.dll如何修复？msvcp140.dll丢失的多种解决方法分享

电脑找不到msvcp140.dll如何修复？msvcp140.dll丢失的多种解决方法分享

在日常电脑操作过程中&#xff0c;用户可能会遇到一个令人困扰的问题&#xff0c;即屏幕上突然弹出一条错误提示&#xff1a;“由于找不到msvcp140.dll&#xff0c;无法继续执行代码”。这一情况往往导致应用程序无法正常启动或运行&#xff0c;给工作和娱乐带来不便。不过&…
阅读更多...
freertos入门---创建FreeRTOS工程

freertos入门---创建FreeRTOS工程

freertos入门—创建FreeRTOS工程 1 STM32CubeMx配置 双击运行STM32CubeMX,在首页选择“ACCESS TO MCU SELECTOR”,如下图所示&#xff1a;   在MCU选型界面&#xff0c;输入自己想要开发的芯片型号&#xff0c;如&#xff1a;STM32F103C8T6: 2 配置时钟 在“System Core”…
阅读更多...
【MATLAB】解决不同版本MATLAB出现中文乱码的问题

【MATLAB】解决不同版本MATLAB出现中文乱码的问题

解决不同版本MATLAB出现中文乱码的问题 方法1&#xff1a;更改保存类型为GBK方法2&#xff1a;记事本打开方法3&#xff1a;Notepad参考 低版本matlab打开高版本Matlab的.m文件时&#xff0c;出现中文乱码问题。比如下图&#xff1a; 出现原因为&#xff1a; 编码格式不统一问…
阅读更多...
【深度学习】第二门课 改善深层神经网络 Week 1 深度学习的实践层面

【深度学习】第二门课 改善深层神经网络 Week 1 深度学习的实践层面

&#x1f680;Write In Front&#x1f680; &#x1f4dd;个人主页&#xff1a;令夏二十三 &#x1f381;欢迎各位→点赞&#x1f44d; 收藏⭐️ 留言&#x1f4dd; &#x1f4e3;系列专栏&#xff1a;深度学习 &#x1f4ac;总结&#xff1a;希望你看完之后&#xff0c;能对…
阅读更多...
力扣---二叉树的锯齿形层序遍历

力扣---二叉树的锯齿形层序遍历

给你二叉树的根节点 root &#xff0c;返回其节点值的 锯齿形层序遍历 。&#xff08;即先从左往右&#xff0c;再从右往左进行下一层遍历&#xff0c;以此类推&#xff0c;层与层之间交替进行&#xff09;。 示例 1&#xff1a; 输入&#xff1a;root [3,9,20,null,null,15,…
阅读更多...
通信光缆主要敷设方式有哪些（续）

通信光缆主要敷设方式有哪些（续）

在《通信光缆主要敷设方式有哪些》一文中&#xff0c;介绍了光缆的直埋、架空和管道敷设方式。此外&#xff0c;根据敷设场景的不同&#xff0c;光缆的常见敷设方式还包括&#xff1a;高铁槽道内敷设、水底敷设、墙壁敷设、引上、室内敷设等。 1 高铁槽道内光缆敷设 光缆顺沿高…
阅读更多...
机器学习每周挑战——二手车车辆信息交易售价数据

机器学习每周挑战——二手车车辆信息交易售价数据

这是数据集的截图 目录 背景描述 数据说明 车型对照&#xff1a; 燃料类型对照&#xff1a; 老规矩&#xff0c;第一步先导入用到的库 第二步&#xff0c;读入数据&#xff1a; 第三步&#xff0c;数据预处理 第四步&#xff1a;对数据的分析 第五步&#xff1a;模型建…
阅读更多...
会声会影电影片头怎么做 会声会影电影质感调色技巧

会声会影电影片头怎么做 会声会影电影质感调色技巧

片头通常通过一系列的图像、音乐和文字等元素来引入电影的主题和氛围。通过视觉和音频的呈现方式&#xff0c;给观众留下深刻的第一印象&#xff0c;为电影的故事铺设基础。这篇文章来学习一下会声会影片头怎么做&#xff0c;会声会影电影质感调色技巧。 一、会声会影电影片头…
阅读更多...
数据库（MySQL）基础：多表查询（一）

数据库（MySQL）基础：多表查询（一）

一、多表关系 概述 项目开发中&#xff0c;在进行数据库表结构设计时&#xff0c;会根据业务需求及业务模块之间的关系&#xff0c;分析并设计表结构&#xff0c;由于业务之间相互关联&#xff0c;所以各个表结构之间也存在着各种联系&#xff0c;基本上分为三种&#xff1a;…
阅读更多...
npm install digital envelope routines::unsupported解决方法

npm install digital envelope routines::unsupported解决方法

目录 一、问题描述二、问题原因三、解决方法 一、问题描述 执行命令 npm install 报错&#xff1a;digital envelope routines::unsupported 二、问题原因 Node.js 17 版本引入了 OpenSSL 3.0&#xff0c;它在算法和密钥大小方面实施了更为严格的限制。这一变化导致 npm 的升…
阅读更多...
badKarma：一款功能强大的网络侦查GUI工具

badKarma：一款功能强大的网络侦查GUI工具

关于badKarma badKarma是一款开源的网络侦查工具&#xff0c;该工具基于Python 3开发&#xff0c;提供了友好的图形化用户接口&#xff0c;可以帮助广大渗透测试人员在网络基础设施安全审计过程中执行网络侦查任务。 badKarma是一个模块化工具&#xff0c;基于python3 GTK套件…
阅读更多...
【研发管理】产品经理知识体系-产品创新流程

【研发管理】产品经理知识体系-产品创新流程

导读&#xff1a;产品创新流程是一个系统性的过程&#xff0c;旨在通过创造和引入新的产品或改进现有产品来满足市场需求、解决用户问题或实现竞争优势。 目录 1、产品创新引论 2、决策基本框架 3、模糊前端 4、产品创新流程模型概论 5、门径管理流程 6、并行工程和集成产…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023